外贸做网站要多久做好高端品牌化妆品排行榜前十名
前言
小亭子正在努力的学习编程,接下来将开启javaEE的学习~~
分享的文章都是学习的笔记和感悟,如有不妥之处希望大佬们批评指正~~
同时如果本文对你有帮助的话,烦请点赞关注支持一波, 感激不尽~~
特别说明:本文分享的代码运行结果不好展示,建议小伙伴们在自己的编译器上跑一下,能更好的观察到执行效果,
运行的时候需要注意一下几点:
1.先运行服务端代码,再运行客户端代码
2.运行的时候注意端口号是否被占用
3.运行的时候注意端口号是否对应
目录
前言
网络编程中的基本概念
发送端和接收端:
请求和响应
客户端和服务端
Socket套接字
分类
数据报套接字:使用传输层UDP协议
流套接字:使用传输层TCP协议
原始套接字
UDP数据报套接字编程
DatagramSocket类
DatagramSocket类构造方法:
DatagramSocket类方法:
DatagramPacket类
DatagramPacket类构造方法
DatagramPacket常用方法
DatagramSocket类成员方法
UDP实现一收一发
UDP实现多收多发
UDP的三种通信方式
UDP如何实现广播
UDP如何实现组播
TCP流套接字编程
Socket构造方法
Socket类成员方法
实现一收一发
实现多收多发
补充一些常见问题:
网络编程中的基本概念
网络编程,指网络上的主机,通过不同的进程,以编程的方式实现网络通信(或称为网络数据传输)。
发送端和接收端:
在一次网络数据传输时:
发送端:数据的发送方进程,称为发送端。发送端主机即网络通信中的源主机。
接收端:数据的接收方进程,称为接收端。接收端主机即网络通信中的目的主机。
收发端:发送端和接收端两端,也简称为收发端。
注意:发送端和接收端只是相对的,只是一次网络数据传输产生数据流向后的概念
请求和响应
一般来说,获取一个网络资源,涉及到两次网络数据传输:
第一次:请求数据的发送
第二次:响应数据的发送
举个栗子:去快餐店吃饭,点了一份蛋炒饭,(相当于发送了请求)
商家说好嘞,马上做(相当于发送了响应)
客户端和服务端
服务端:在常见的网络数据传输场景下,把提供服务的一方进程,称为服务端,可以提供对外服务。
客户端:获取服务的一方进程,称为客户端
常见的客户端服务端模型
最常见的场景,客户端是指给用户使用的程序,服务端是提供用户服务的程序:
1. 客户端先发送请求到服务端
2. 服务端根据请求数据,执行相应的业务处理
3. 服务端返回响应:发送业务处理结果
4. 客户端根据响应数据,展示处理结果(展示获取的资源,或提示保存资源的处理结果)
Socket套接字
Socket套接字,是由系统提供用于网络通信的技术,是基于TCP/IP协议的网络通信的基本操作单元,基于Socket套接字的网络开发程序开发就是网络编程。
分类
Socket套接字主要针对传输层协议划分为如下三类:
数据报套接字:使用传输层UDP协议
UDP,即User Datagram Protocol(用户数据报协议),传输层协议。
以下为UDP的特点(细节后续再学习):
无连接
不可靠传输
面向数据报
有接收缓冲区,无发送缓冲区
大小受限:一次最多传输64k可以广播发送 ,发送数据结束时无需释放资源,开销小,速度快
对于数据报来说,可以简单的理解为,传输数据是一块一块的,发送一块数据假如100个字节,必须一次发送,接收也必须一次接收100个字节,而不能分100次,每次接收1个字节。UDP协议通信场景
语音通话,视频会话等
流套接字:使用传输层TCP协议
TCP,即Transmission Control Protocol(传输控制协议),传输层协议。
以下为TCP的特点:
有连接
可靠传输
面向字节流
有接收缓冲区,也有发送缓冲区
大小不限全双工通信:一条路径,但是路径两方都可以对话。(双向对话)
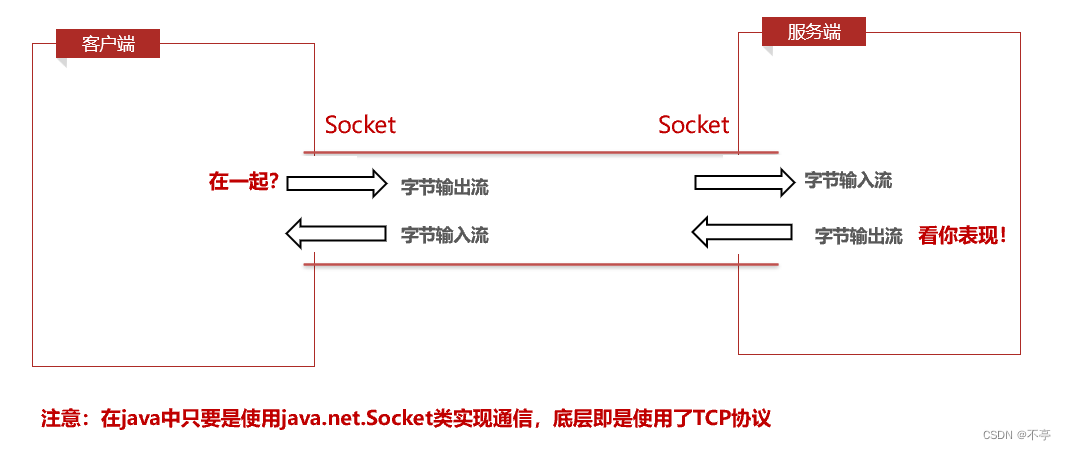
对于字节流来说,可以简单的理解为,传输数据是基于IO流,流式数据的特征就是在IO流没有关闭的情况下,是无边界的数据,可以多次发送,也可以分开多次接收。TCP协议通信场景
对信息安全要求较高的场景,例如:文件下载、金融等数据通信。TCP通信模式演示:
原始套接字
原始套接字用于自定义传输层协议,用于读写内核没有处理的IP协议数据。
(这个知道就行)
UDP数据报套接字编程
UDP套接字API
UDP套接字的API中主要包括两个类 :
- 1.DatagramSocket
- 2.DatagramPacket
DatagramSocket类
DatagramSocket类就是实例一个UDP版本的套接字也是就数据包套接字。
Socket对象对应到系统中的一个特殊文件(socket文件),socket文件不是数据存储区域的一部分,而是对应到网卡这个硬件设备,(因为网卡是一个硬件,对于代码而已,不好直接操作,因此将它抽象成了一个文件进行间接操作。)
DatagramSocket类构造方法:
| 方法签名 | 方法说明 |
|---|---|
| DatagramSocket() | 创建一个UDP数据报套接字的Socket,绑定到本机任意一个随机端口 (一般用于客户端) |
| DatagramSocket(int port) | 创建一个UDP数据报套接字的Socket,绑定到本机指定的端口(一般用 于服务端) |
DatagramSocket类方法:
| 方法签名 | 方法说明 |
| void receive(DatagramPacket p) | 从此套接字接收数据报(如果没有接收到数据报,该方法会阻塞等待) |
| void send(DatagramPacketp) | 从此套接字发送数据报包(不会阻塞等待,直接发送) |
| void close() | 关闭此数据报套接字 |
receive方法:它的参数需要准备一个空的DatagramPacket对象(对象需要给予存储空间),它把DatagramPacket实例对象再装入到准备好的空的DatagramPacket对象中去
(举个栗子:当我们盛饭时,需要一个空的碗)
send方法他是DatagramPacket实例对象载入到接收缓冲区。
close方法,因为DatagramSocket类属于文件资源,当我们不用的时候,我们需要将它给手动关闭了。
DatagramPacket类
DatagramPacket是UDP Socket发送和接收的数据报。
DatagramPacket类构造方法
| 构造器 | 说明 |
| public DatagramPacket(byte[] buf, int length, InetAddress address, int port) | 创建发送端数据包对象 buf:要发送的内容,字节数组 length:要发送内容的字节长度 address:接收端的IP地址对象 port:接收端的端口号 |
| public DatagramPacket(byte[] buf, int length) | 创建接收端的数据包对象 buf:用来存储接收的内容 length:能够接收内容的长度 |
DatagramPacket常用方法
| 方法 | 说明 |
| InetAddress getAddress() | 从接收的数据报中,获取发送端主机IP地址;或从发送的数据报中,获取 接收端主机IP地址 |
| int getPort() | 从接收的数据报中,获取发送端主机的端口号;或从发送的数据报中,获 取接收端主机端口号 |
| byte[] getData() | 获取数据报中的数据 |
| int getLength() | 获得实际接收到的字节个数 |
DatagramSocket类成员方法
| 方法 | 说明 |
| public void send(DatagramPacket dp) | 发送数据包 |
| public void receive(DatagramPacket p) | 接收数据包 |
UDP实现一收一发
服务端实现思路:
- 创建DatagramSocket对象并指定端口(接收端对象) 【接韭菜的人】
- 创建DatagramPacket对象接收数据(数据包对象) 【韭菜盘子】
- 使用DatagramSocket对象的receive方法传入DatagramPacket对象【开始接收韭菜】
- 释放资源
代码实现:
public class ServerDemo2 {public static void main(String[] args) throws Exception {System.out.println("=====服务端启动======");// 1、创建接收端对象:注册端口(人)DatagramSocket socket = new DatagramSocket(8888);// 2、创建一个数据包对象接收数据(韭菜盘子)byte[] buffer = new byte[1024 * 64];DatagramPacket packet = new DatagramPacket(buffer, buffer.length);// 3、等待接收数据。socket.receive(packet);// 4、取出数据即可// 读取多少倒出多少int len = packet.getLength();String rs = new String(buffer,0, len);System.out.println("收到了:" + rs);// 获取发送端的ip和端口String ip =packet.getSocketAddress().toString();System.out.println("对方地址:" + ip);int port = packet.getPort();System.out.println("对方端口:" + port);//关闭资源socket.close();} }
客户端实现思路:
- 创建DatagramSocket对象(发送端对象) 【扔韭菜的人】
- 创建DatagramPacket对象封装需要发送的数据(数据包对象) 【 韭菜盘子】
- 使用DatagramSocket对象的send方法传入DatagramPacket对象 【开始抛出韭菜】
- 释放资源
代码实现:
public class ClientDemo1 {public static void main(String[] args) throws Exception {System.out.println("=====客户端启动======");// 1、创建发送端对象:发送端自带默认的端口号(人)DatagramSocket socket = new DatagramSocket(6666);// 2、创建一个数据包对象封装数据(韭菜盘子)/**public DatagramPacket(byte buf[], int length,InetAddress address, int port)参数一:封装要发送的数据(韭菜)参数二:发送数据的大小参数三:服务端的主机IP地址参数四:服务端的端口*/byte[] buffer = "我是一颗快乐的韭菜,你愿意吃吗?".getBytes();DatagramPacket packet = new DatagramPacket( buffer, buffer.length,InetAddress.getLocalHost() , 8888);// 3、发送数据出去socket.send(packet);socket.close();} }
UDP实现多收多发
需求:
①发送端可以一直发送消息。
②接收端可以不断的接收多个发送端的消息展示。
③发送端输入了exit则结束发送端程序。
客户端实现步骤
- 创建DatagramSocket对象(发送端对象)【扔韭菜的人】
- 使用while死循环不断的接收用户的数据输入,如果用户输入的exit则退出程序
- 如果用户输入的不是exit, 把数据封装成DatagramPacket 【 韭菜盘子】
- 使用DatagramSocket对象的send方法将数据包对象进行发送 【开始抛出韭菜】
- 释放资源
代码实现:
public class ClientDemo1 {public static void main(String[] args) throws Exception {System.out.println("=====客户端启动======");// 1、创建发送端对象:发送端自带默认的端口号(人)DatagramSocket socket = new DatagramSocket(7777);Scanner sc = new Scanner(System.in);while (true) {System.out.println("请说:");String msg = sc.nextLine();if("exit".equals(msg)){System.out.println("离线成功!");socket.close();break;}// 2、创建一个数据包对象封装数据(韭菜盘子)byte[] buffer = msg.getBytes();DatagramPacket packet = new DatagramPacket( buffer, buffer.length,InetAddress.getLocalHost() , 8888);// 3、发送数据出去socket.send(packet);}} }
接收端实现步骤
- 创建DatagramSocket对象并指定端口(接收端对象) 【接韭菜的人】
- 创建DatagramPacket对象接收数据(数据包对象) 【韭菜盘子】
- 使用while死循环不断的进行第4步
- 使用DatagramSocket对象的receive方法传入DatagramPacket对象【开始接收韭菜】
代码实现:
public class ServerDemo2 {public static void main(String[] args) throws Exception {System.out.println("=====服务端启动======");// 1、创建接收端对象:注册端口(人)DatagramSocket socket = new DatagramSocket(8888);// 2、创建一个数据包对象接收数据(韭菜盘子)byte[] buffer = new byte[1024 * 64];DatagramPacket packet = new DatagramPacket(buffer, buffer.length);while (true) {// 3、等待接收数据。socket.receive(packet);// 4、取出数据即可// 读取多少倒出多少int len = packet.getLength();String rs = new String(buffer,0, len);System.out.println("收到了来自:" + packet.getAddress() +", 对方端口是" + packet.getPort() +"的消息:" + rs);}} }
UDP的三种通信方式
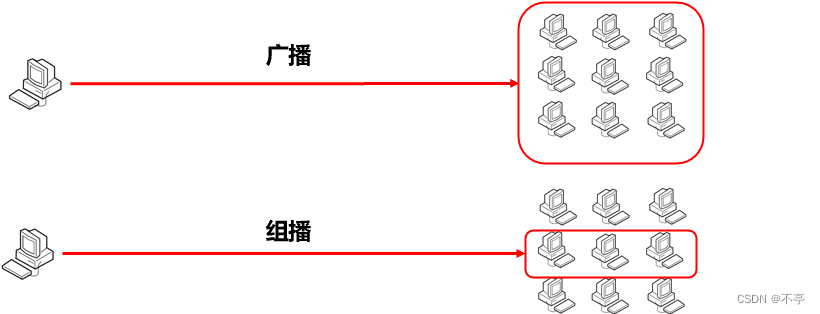
- 单播:单台主机与单台主机之间的通信。
- 广播:当前主机与所在网络中的所有主机通信。
- 组播:当前主机与选定的一组主机的通信。
UDP如何实现广播
使用广播地址:255.255.255.255
具体操作:
①发送端发送的数据包的目的地写的是广播地址、且指定端口。 (255.255.255.255 , 9999)
②本机所在网段的其他主机的程序只要注册对应端口就可以收到消息了。(9999)
UDP如何实现组播
使用组播地址:224.0.0.0 ~ 239.255.255.255
具体操作:
①发送端的数据包的目的地是组播IP (例如:224.0.1.1, 端口:9999)
②接收端必须绑定该组播IP(224.0.1.1),端口还要注册发送端的目的端口9999 ,这样即可接收该组播消息。
③DatagramSocket的子类MulticastSocket可以在接收端绑定组播IP。
TCP流套接字编程
Socket构造方法
| 构造器 | 说明 |
| public Socket(String host , int port) | 创建发送端的Socket对象与服务端连接,参数为服务端程序的ip和端口。 |
| public ServerSocket(int port) | 注册服务端端口 |
Socket类成员方法
| 方法 | 说明 |
| OutputStream getOutputStream() | 获得字节输出流对象 |
| InputStream getInputStream() | 获得字节输入流对象 |
| public Socket accept() | 等待接收客户端的Socket通信连接 连接成功返回Socket对象与客户端建立端到端通信 |
实现一收一发
服务端实现步骤
- 创建ServerSocket对象,注册服务端端口。
- 调用ServerSocket对象的accept()方法,等待客户端的连接,并得到Socket管道对象。
- 通过Socket对象调用getInputStream()方法得到字节输入流、完成数据的接收。
- 释放资源:关闭socket管道
代码实现:
/**目标:开发Socket网络编程入门代码的服务端,实现接收消息*/ public class ServerDemo2 {public static void main(String[] args) {try {System.out.println("===服务端启动成功===");// 1、注册端口ServerSocket serverSocket = new ServerSocket(7777);// 2、必须调用accept方法:等待接收客户端的Socket连接请求,建立Socket通信管道Socket socket = serverSocket.accept();// 3、从socket通信管道中得到一个字节输入流InputStream is = socket.getInputStream();// 4、把字节输入流包装成缓冲字符输入流进行消息的接收BufferedReader br = new BufferedReader(new InputStreamReader(is));// 5、按照行读取消息String msg;if ((msg = br.readLine()) != null){System.out.println(socket.getRemoteSocketAddress() + "说了:: " + msg);}} catch (Exception e) {e.printStackTrace();}} }
客户端实现步骤
- 创建客户端的Socket对象,请求与服务端的连接。
- 使用socket对象调用getOutputStream()方法得到字节输出流。
- 使用字节输出流完成数据的发送。
- 释放资源:关闭socket管道。
代码实现:public class ClientDemo1 {public static void main(String[] args) {try {System.out.println("====客户端启动===");// 1、创建Socket通信管道请求有服务端的连接// public Socket(String host, int port)// 参数一:服务端的IP地址// 参数二:服务端的端口Socket socket = new Socket("127.0.0.1", 7777);// 2、从socket通信管道中得到一个字节输出流 负责发送数据OutputStream os = socket.getOutputStream();// 3、把低级的字节流包装成打印流PrintStream ps = new PrintStream(os);// 4、发送消息ps.println("我是TCP的客户端,我已经与你对接,并发出邀请:约吗?");ps.flush();// 关闭资源。// socket.close();} catch (Exception e) {e.printStackTrace();}} }
实现多收多发
需求:使用TCP通信方式实现:多发多收消息。
具体要求:
解决方法:需要引入多线程
- 主线程定义了循环负责接收客户端Socket管道连接
- 每接收到一个Socket通信管道后分配一个独立的线程负责处理它
客户端实现代码:
/**目标:实现服务端可以同时处理多个客户端的消息。*/ public class ClientDemo1 {public static void main(String[] args) {try {System.out.println("====客户端启动===");// 1、创建Socket通信管道请求有服务端的连接// public Socket(String host, int port)// 参数一:服务端的IP地址// 参数二:服务端的端口Socket socket = new Socket("127.0.0.1", 7777);// 2、从socket通信管道中得到一个字节输出流 负责发送数据OutputStream os = socket.getOutputStream();// 3、把低级的字节流包装成打印流PrintStream ps = new PrintStream(os);Scanner sc = new Scanner(System.in);while (true) {System.out.println("请说:");String msg = sc.nextLine();// 4、发送消息ps.println(msg);ps.flush();}// 关闭资源。不建议写在这// socket.close();} catch (Exception e) {e.printStackTrace();}} }服务端实现代码:
**目标:实现服务端可以同时处理多个客户端的消息。*/ public class ServerDemo2 {public static void main(String[] args) {try {System.out.println("===服务端启动成功===");// 1、注册端口ServerSocket serverSocket = new ServerSocket(7777);// a.定义一个死循环由主线程负责不断的接收客户端的Socket管道连接。while (true) {// 2、每接收到一个客户端的Socket管道,交给一个独立的子线程负责读取消息Socket socket = serverSocket.accept();System.out.println(socket.getRemoteSocketAddress()+ "它来了,上线了!");// 3、开始创建独立线程处理socketnew ServerReaderThread(socket).start();}} catch (Exception e) {e.printStackTrace();}} }独立线程实现处理socket
public class ServerReaderThread extends Thread{private Socket socket;public ServerReaderThread(Socket socket){this.socket = socket;}@Overridepublic void run() {try {// 3、从socket通信管道中得到一个字节输入流InputStream is = socket.getInputStream();// 4、把字节输入流包装成缓冲字符输入流进行消息的接收BufferedReader br = new BufferedReader(new InputStreamReader(is));// 5、按照行读取消息String msg;while ((msg = br.readLine()) != null){System.out.println(socket.getRemoteSocketAddress() + "说了:: " + msg);}} catch (Exception e) {System.out.println(socket.getRemoteSocketAddress() + "下线了!!!");}} }
上述通信模型架构存在什么问题呢?
答:每个客户端发送请求都要创建一个新的线程
客户端与服务端的线程模型是: N-N的关系。
客户端并发越多,系统瘫痪的越快。
那么如何解决呢?
我们之前分享多线程的时候说过线程池这个概念,线程池可以有效降低创建和关闭线程所使用的的资源,那么接下来我们就用线程池去优化这个通信模型。
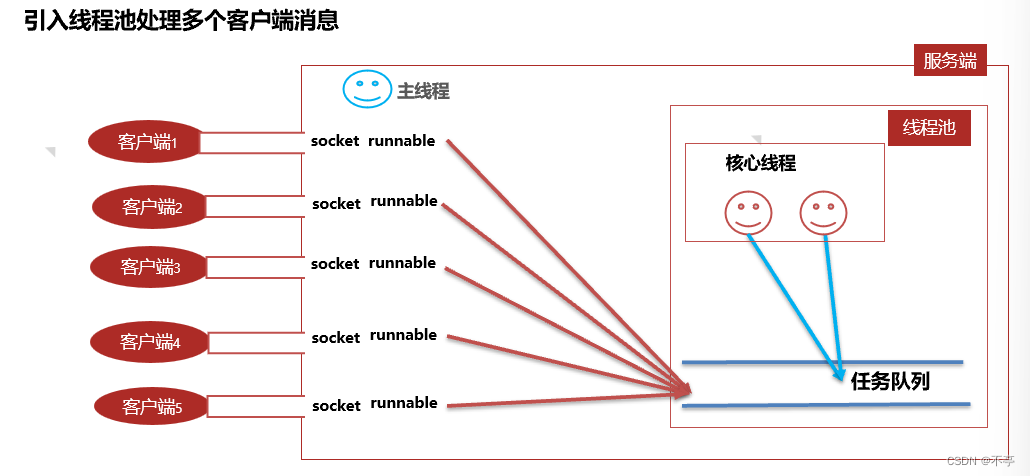
服务端可以复用线程处理多个客户端,可以避免系统瘫痪。适合客户端通信时长较短的场景。
使用线程池进行优化,客户端不用进行修改,主要修改服务端和创建线程池
服务端代码实现:
/**目标:实现服务端可以同时处理多个客户端的消息。*/ public class ServerDemo2 {// 使用静态变量记住一个线程池对象private static ExecutorService pool = new ThreadPoolExecutor(300,1500, 6, TimeUnit.SECONDS,new ArrayBlockingQueue<>(2), Executors.defaultThreadFactory(), new ThreadPoolExecutor.AbortPolicy());public static void main(String[] args) {try {System.out.println("===服务端启动成功===");// 1、注册端口ServerSocket serverSocket = new ServerSocket(6666);// a.定义一个死循环由主线程负责不断的接收客户端的Socket管道连接。while (true) {// 2、每接收到一个客户端的Socket管道,Socket socket = serverSocket.accept();System.out.println(socket.getRemoteSocketAddress()+ "它来了,上线了!");// 任务对象负责读取消息。Runnable target = new ServerReaderRunnable(socket);pool.execute(target);}} catch (Exception e) {e.printStackTrace();}} }线程池代码实现:
public class ServerReaderRunnable implements Runnable{private Socket socket;public ServerReaderRunnable(Socket socket){this.socket = socket;}@Overridepublic void run() {try {// 3、从socket通信管道中得到一个字节输入流InputStream is = socket.getInputStream();// 4、把字节输入流包装成缓冲字符输入流进行消息的接收BufferedReader br = new BufferedReader(new InputStreamReader(is));// 5、按照行读取消息String msg;while ((msg = br.readLine()) != null){System.out.println(socket.getRemoteSocketAddress() + "说了:: " + msg);}} catch (Exception e) {System.out.println(socket.getRemoteSocketAddress() + "下线了!!!");}} }
补充一些常见问题:
1.ideal默认只能启动一个客户端,当我们要启动多个客户端测试的时候该怎么做呢?
右键——>
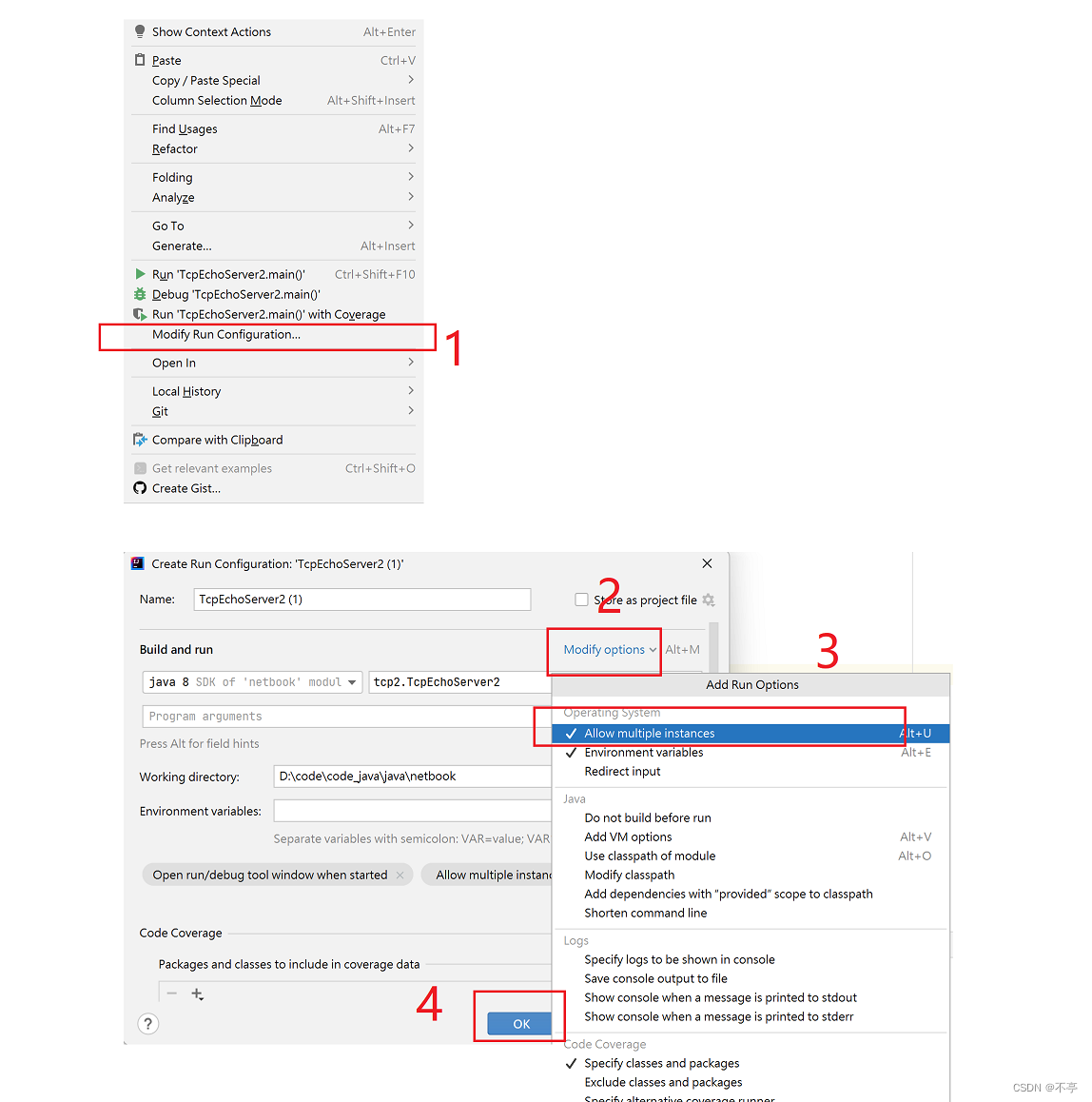
2.端口被占用报错
如果一个进程A已经绑定了一个端口,再启动一个进程B绑定该端口,就会报错,这种情况也叫端
口被占用。对于java进程来说,端口被占用的常见报错信息如下: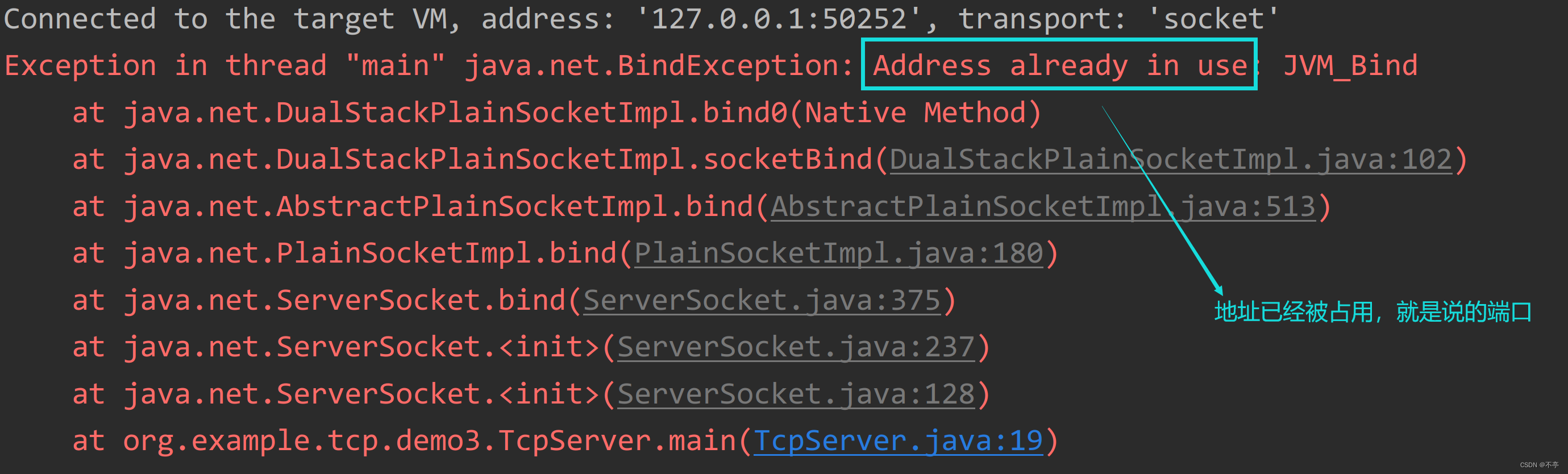
此时需要检查进程B绑定的是哪个端口,再查看该端口被哪个进程占用。以下为通过端口号查进程
的方式:
在cmd输入 netstat -ano | findstr 端口号 ,则可以显示对应进程的pid。如以下命令显
示了8888进程的pid

在任务管理器中,通过pid查找进程
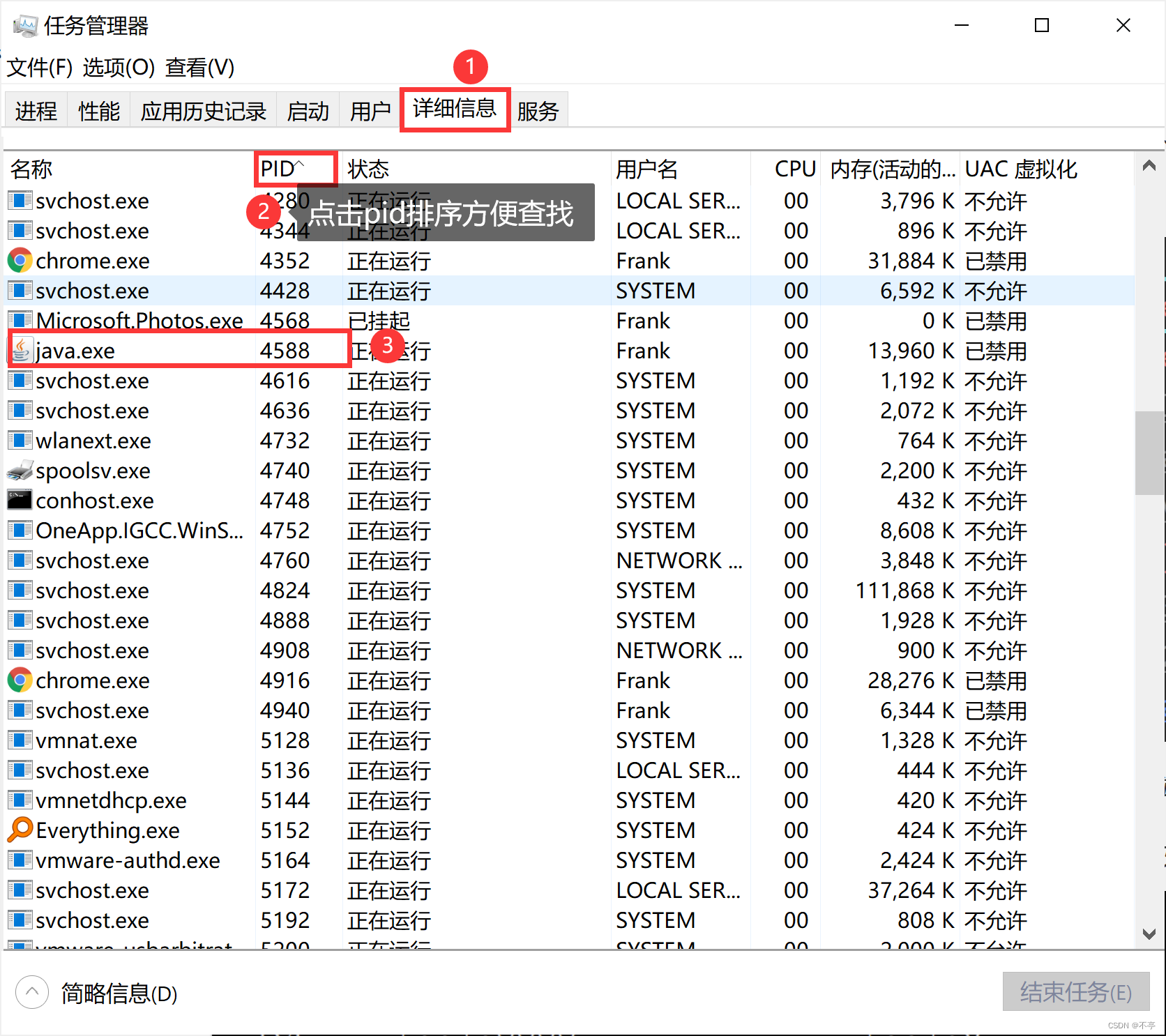
解决端口被占用的问题:
如果占用端口的进程A不需要运行,就可以关闭A后,再启动需要绑定该端口的进程B
如果需要运行A进程,则可以修改进程B的绑定端口,换为其他没有使用的端口。
以上就是本文的全部内容,下一篇文章将分享网络编程的简单应用:即时通信的实现,字典客户端和字典服务器的实现,一键三连,和小亭子一起学编程呀~~~