网站主题及样式优化可以做直播卖产品的网站
近日,国产思维导图软件——亿图脑图MindMaster发布了全新版本V10.9.0,本次亿图脑图的升级给用户带来了极大的惊喜。全新升级的亿图脑图MindMaster不仅支持20+格式的文件智能解析成思维导图,还支持思维导图一键生成PPT、音频、视频等内容形式;此外,亿图脑图独家首发文本编辑实时布局功能,位于行业内领先水平。本次升级的亿图脑图MindMaster就如同一个多模态的中枢处理器,拓宽了思维导图的边界。
一做PPT就头疼?亿图脑图帮你一键生成
有人会说,思维导图的形式只能作为一种可视化表达方式,输出的格式比较单一。而亿图脑图MindMaster V10.9.0打破了单一的导出方式,支持思维导图一键生成PPT,帮助用户更好地表达思想,展示成果,传播信息。用户可以提供大纲框架,或者思维导图,剩下的就交给亿图脑图,只需不到30秒,就可以生成一份高质量的PPT,亿图脑图支持思维导图、大纲模式、PPT模式这三种模式之间丝滑切换,用户可以将生成的PPT文件下载到本地,再进行编辑和修改,大大地提升了PPT的制作效率。除了支持思维导图一键生成PPT之外,也支持输入关键词一键智能生成PPT。当前,亿图脑图提供20种高颜值PPT主题模板,用户可以在思维导图进行导出的时候选择自己喜欢的风格类型。

可以“听”的思维导图,满足多场景听信息的需求
亿图脑图MindMaster除了可以导出PPT的格式之外,还支持导出音频(wav格式)。我们知道,在获取信息的时候,文字的阅读速度肯定是比音频效率更高的,但是我们不可否认,在开车、运动、睡觉前等一些特定场景中,音频的优势更加明显。如果用户想要在一个不方便阅读的场景下,获取信息,同时不影响当前的使用的场景,那么可以“听”的思维导图就能满足他的需求。亿图脑图不仅支持按照思维导图的原本内容导出音频,还支持对思维导图的原文内容进行总结和改写。如果你是一名公司高层,在开车的过程当中想要听取内容重点,亿图脑图支持对思维导图进行智能总结提炼出核心观点生成音频;如果你是一名家长,要在睡前给小孩讲故事,亿图脑图支持对思维导图进行故事线的内容的音频生成。
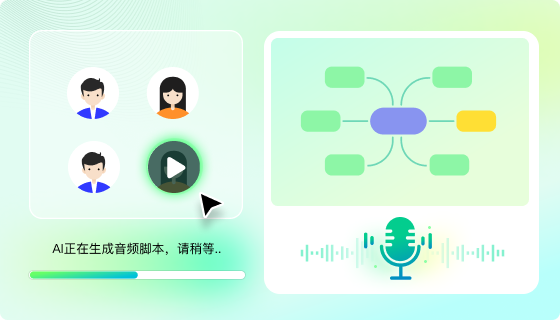
思维导图转视频,亿图脑图让内容“生动”起来
总所周知,视频作为一种易于传播且被大众接受的内容形式,在传递知识、提供信息、辅助表达上面能够很好的让信息的接受者理解传播者的价值表达。亿图脑图MindMaster同样也支持思维导图一键导出视频格式。对于短视频传播以及教学知识分享有需求的用户来说,思维导图转视频的功能无疑帮助大家提高了内容的生产效率,通过“生动”的思维导图、配合节奏感的声音,将内容要点清晰有序并且动态地呈现在受众面前,让内容表达更有说服力。

文件智能解析,亿图脑图化身“知识加工厂”
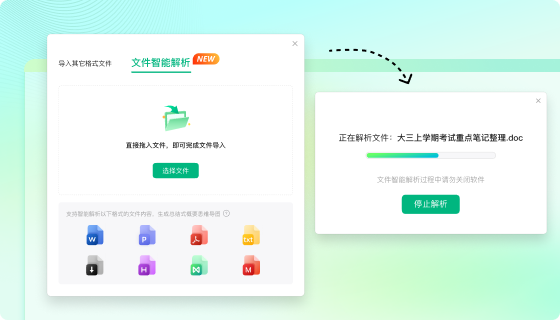
在思维导图用户中,不乏很多科研工作者、医学生、心理咨询师以及文字、教育工作者。对于他们而言,如何在短时间内阅读大量文献,并进行总结思考归纳是每次学习都要做的事情。为此,亿图脑图MindMaster本次上线的智能文件解析功能,一万字以内的文本内容快速生成总结性思维导图。用户不用花费大量的时间和精力手动总结文本内容,只须上传目标文档,亿图脑图的智能解析工具就能快速创建一个清晰明了的思维导图,用户可以通过阅读思维导图,迅速理清思路,抓住文章重点,提高学习效率。亿图脑图支持20+格式的文档直接智能解析成思维导图(包括word、txt、图片、表格、PDF等多种格式)。
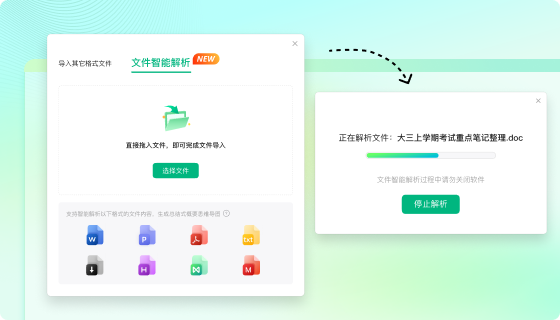
文本编辑实时布局,亿图脑图编辑性能领先行业水平
在这一次的版本更新中,亿图脑图MindMaster对节点编辑器进行了重构,极大的提升了思维导图的编辑性能。这一能力的提升,意味着亿图脑图的编辑性能领先行业水平。在之前的版本中,用户在编辑思维导图的主题或子主题的时候,需要等内容全部输入完成之后,按回车键确定,布局才会发生改变。现在,我们每进行一步内容编辑的时候,都会实时布局,大大提升了用户的编辑时的视觉体验,同时,也可以让导图的布局呈现更加精准。这一功能的实现,对于产品的性能要求很高,亿图脑图MindMaster可以做到。
亿图脑图MindMaster,以其独特的产品功能和优势,已经在市场上赢得了广大用户的喜爱。亿图脑图MindMasterPC端V10.9.0的发布,对思维导图软件功能的突破与探索,意味着亿图在行业内的创新能力处于领先水平。期待在未来,亿图脑图MindMadster能为更多的用户提供更智能、更优质的使用体验。
