网站免费加速器怎么用wordpress建手机网站
Si24R2F+是针对IOT应用领域推出的新款超低功耗2.4G内置NVM单发射芯片。广泛应用于2.4G有源活体动物耳标,带实时测温+计步功能。相较于Si24R2E,Si24R2F+增加了温度监控、自动唤醒间隔功能;发射功率由7dBm增加到12dBm,距离更远;关断电流由700nA降到500nA,功耗更低。可兼容Si24R2E,性能更加强悍。
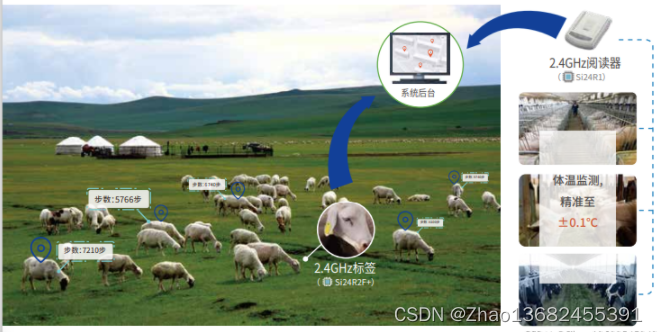
Si24R2F+是针对IOT应用领域推出的新款超低功耗2.4G内置NVM单发射芯片。广泛应用于2.4G有源活体动物耳标,带实时测温+计步功能。相较于Si24R2E,Si24R2F+增加了温度监控、自动唤醒间隔功能;发射功率由7dBm增加到12dBm,距离更远;关断电流由700nA降到500nA,功耗更低。可兼容Si24R2E,性能更加强悍。
