asp.net做学校网站首页企业logo商标
好久没更新了
学习的内容太多了有点杂
一时不知道从何说起 !!!
对于Django我也不是很了解
在网上搜了个词条就是以下显示
我目前的了解也仅限于此
希望在接下来的学习过程中
有更多的学习体会可以和大家分享

一涉及到在对应python环境
下载东西时思维就会很混乱
这里再把之前的
切换python环境的方法复习一下
我的电脑里有两个python环境
一个是3.8.3(Anaconda3自带python环境)
一个是3.10.4
为了我记忆清晰
我都下载到了F盘

首先要在cmd窗口将路径
转换到你python放的盘的路径下面
大家学习的内容会越来越多
一定要将文件目录设置的规范
方便自己后续学习查找!
C:\WINDOWS\system32>F: #这里是将cmd的路径转到F盘下(不区分大小写)F:\>cd F:\Anaconda3 #将python转到3.8.3F:\Anaconda3>python #确定python版本
以上我的原始默认
python版本其实是3.10.4
只是很久不操作技术有些生疏
为了把笔记写准确不误导大家
我就又练习了一下
我需要的就是3.10.4环境
但是我有点不会举一反三
我就想试一下这会儿熟练了许多
又将环境转回来了

确定好相应的python环境
开始在该python环境下安装django
pip install django==3.2.0 -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com上学期安装第三方库的方法还是很香
希望大家要多总结经验 !
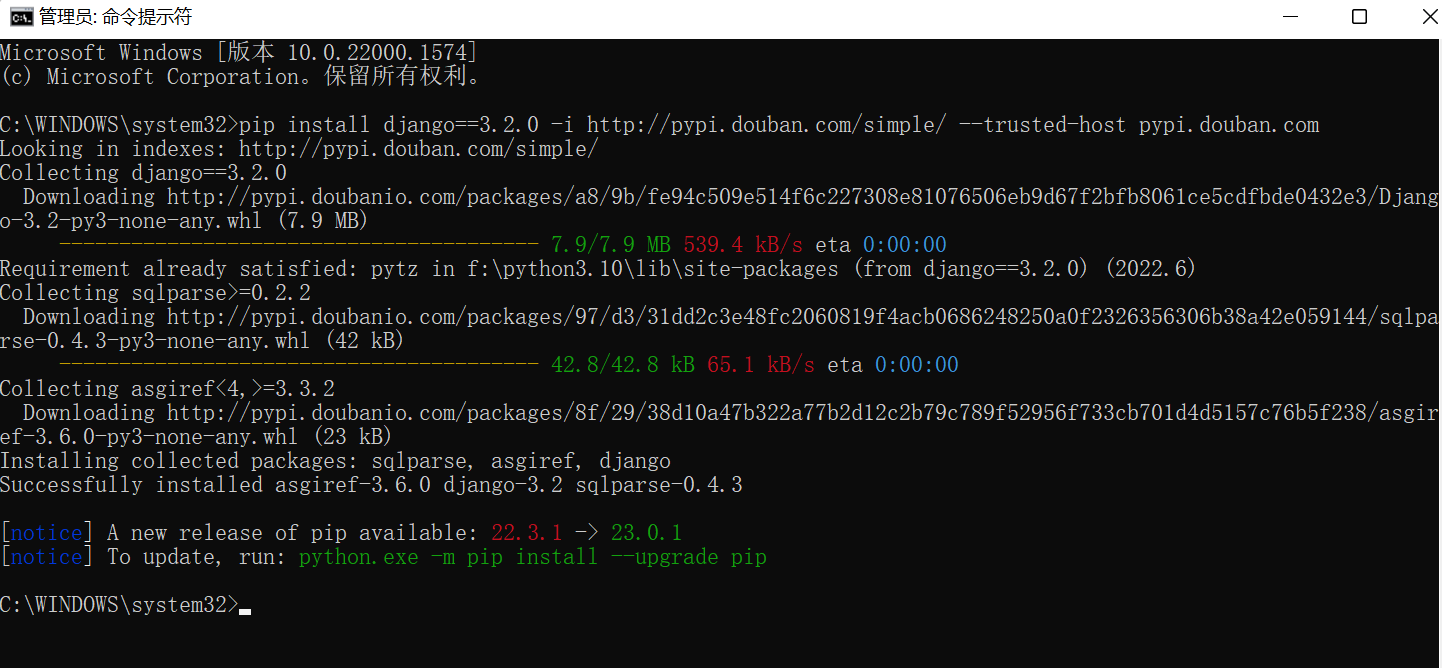
老师讲解说django是个第三方模块
根据以往安装第三方库的经验
确实是个第三方库
我在这里总结一遍的原因是
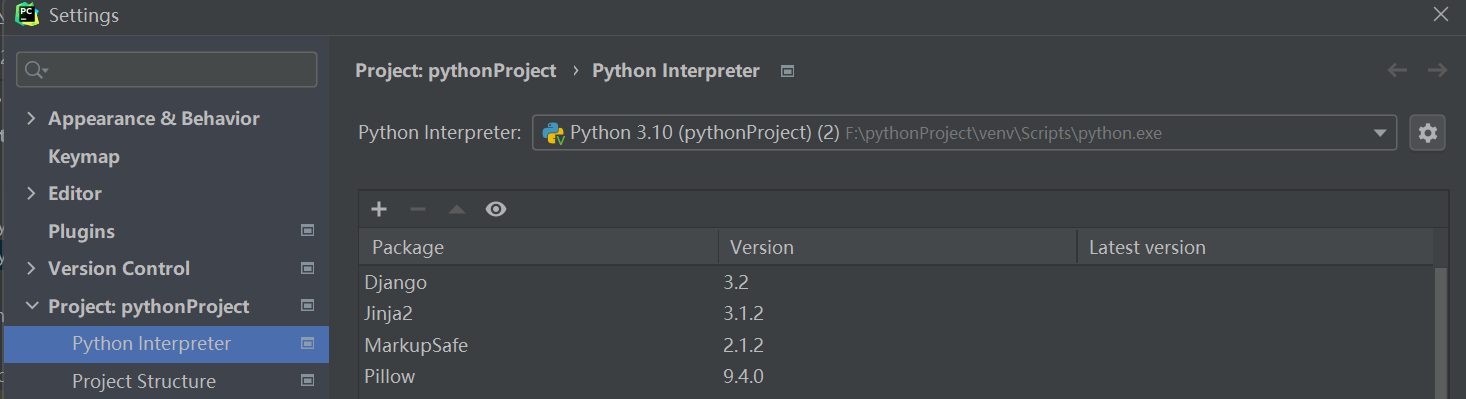
我在pycharm的终端中下载了
环境我看了也是对的
也在pycharm的库包中发现了django包
但是在我的python3.10的安装目录下
并没有出现对应的django包和.exe文件
因此我只能在命令提示符中
试着再下载一遍
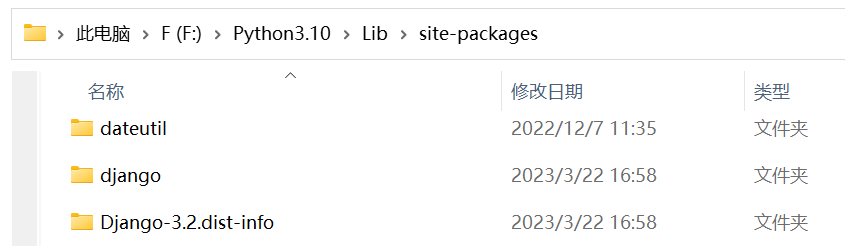
这回python3.10的安装目录下有了
在Lib文件下的site-packages中看第三方库
django[框架的源码]
在Scripts中看.exe文件
django-admin.exe
[工具,创建django项目中的文件和文件夹]
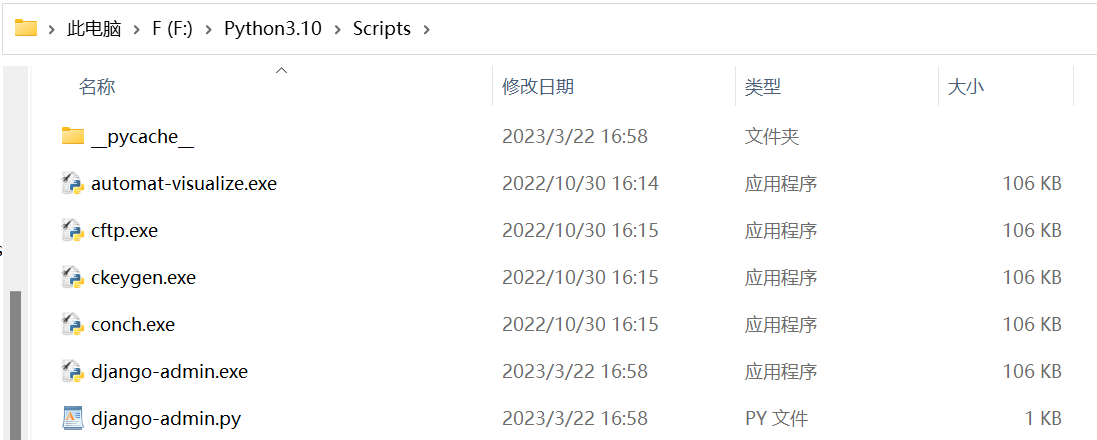
如果在python的安装目录下的
Scripts文件下有django-admin.exe
Lib文件下有django
那就证明安装成功!!!
我的意思是如果在pycharm终端安装不好
不妨试试在命令提示符(即cmd界面)试试!
小tips:
图片在手机端看会模糊
大家要想看清楚可以在电脑上看会清晰呦!!!
