金华网站建设方案优化南昌手机网站制作
OLAP引擎面临的挑战

常见OLAP引擎对比

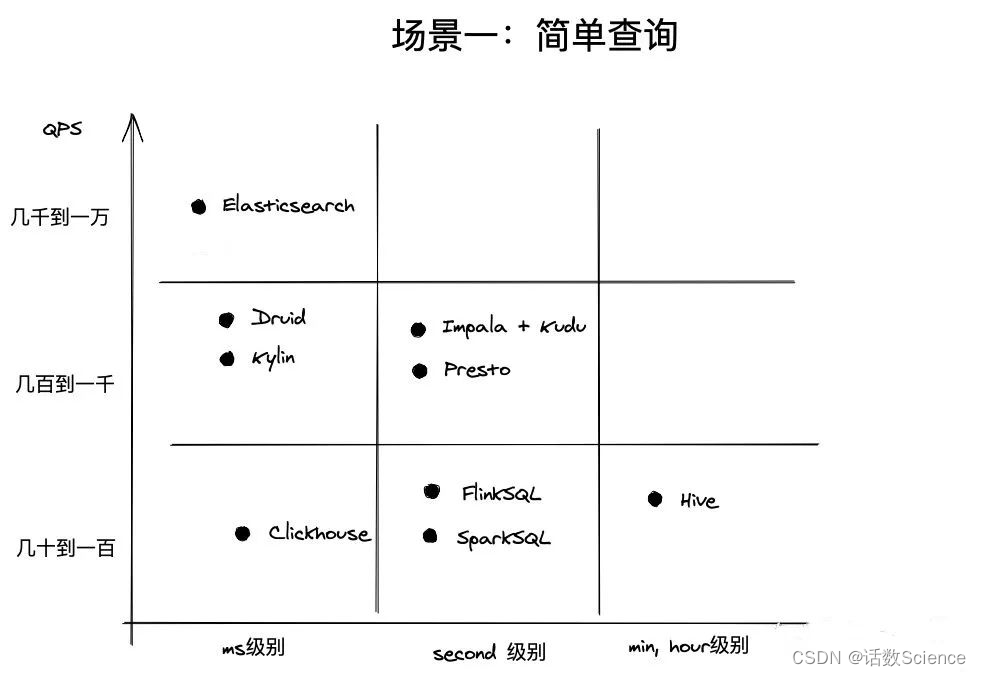
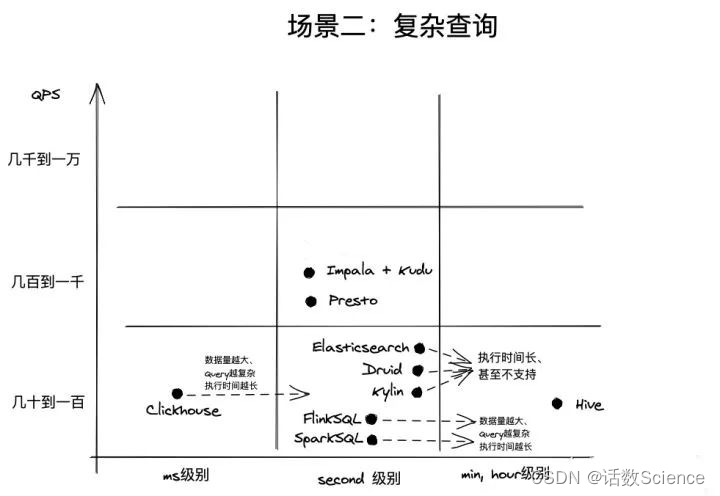
OLAP分析场景中,一般认为QPS达到1000+就算高并发,而不是像电商、抢红包等业务场景中,10W以上才算高并发,毕竟数据分析场景,数据海量,计算复杂,QPS能够达到1000已经非常不容易
| 原理 | 优势 | 劣势 | |
| Clickhouse | Clickhouse用C++实现,具备强劲的查询性能。 比较适合内部BI报表型应用。 不适合如数十万的广告主报表或者数百万的淘宝店主相关报表应用。 如果如数据量是TB级别,聚合计算稍复杂一点,单集群QPS一般达到100已经很困难了 | clickhouse的优势是单个查询执行速度更快,不依赖hadoop,架构和运维更简单。 它比较擅长的地方是对一个大数据量的单表进行聚合查询。 可以提供低延迟(ms级别)的响应速度。 | 应该避免把它作为多表关联查询(JOIN)的引擎,也应该避免把它用在期望支撑高并发数据查询的场景。 ClickHouse的问题是使用门槛高、运维成本高和分布式能力太弱,需要较多的定制化和较深的技术实力。 |
| StarRocks | StarRocks 是一款极速全场景 MPP 企业级数据库产品,具备水平在线扩缩容,金融级高可用,兼容 MySQL 协议和 MySQL 生态,提供全面向量化引擎与多种数据源联邦查询等重要特性。StarRocks 致力于在全场景 OLAP 业务上为用户提供统一的解决方案,适用于对性能,实时性,并发能力和灵活性有较高要求的各类应用场景。 StarRocks号称新一代全场景MPP数据库,客观而言,其场景适应性确实非常强,在离线、实时分析上的表现都非常突出,很多大厂都用它实现了引擎的收敛,精简了数据架构。 | StarRocks最初主要的优势是性能,当时在单表查询方面与性能标杆ClickHouse不相上下,而join优化特性使其在多表关联查询场景下的性能表现要远远优于ClickHouse,替换ClickHouse自然也就成了StarRocks的第一个目标。 而StarRocks的野心不止于此,后来又进一步发展了联邦查询功能,成为Presto。 2023年推出了存算分离架构,据说最高可让存储成本下降80%。 | |
| Doris | 亚秒级响应,1万+QPS 预聚合技术,支持高效的多维分析,多表关联分析 | Hadoop 虽然解决了很多大数据的问题,但是其安装、配置和运维的复杂性也让人们望而却步;鉴于此,他们想设计出一个安装部署和开发运维都极具简单的一个系统。 首先就是减少组件,减少到两个,前端 FE 和后端 BE。FE 是 JAVA 代码实现的,BE 是 C++ 代码。 这个 BE 分布式管理框架,可以自动的管理数据副本的分布、进行修复和均衡。比如对于副本损坏的情况,Doris会自动感知并进行修复。 无论 FE 还是 BE 都能通过一条简单的 SQL 命令实现水平扩缩容。当然通过腾讯云管控的话,你就是去点一下鼠标, Doris 就会迅速扩缩容。 另外就是减少依赖,Doris 的设计目标是完全不依赖第三方系统。 | 多租户管理ClickHouse的权限和Quota的粒度更细,Doris要差一些, 支持部分RBAC, 不支持行级别权限; Doris的问题是性能差一些可靠性差一些。 |
| Elasticsearch | |||
| Impala | Impala是Cloudera公司主导开发的新型查询系统,它提供SQL语义,能查询存储在Hadoop的HDFS和HBase中的PB级大数据。已有的Hive系统虽然也提供了SQL语义,但由于Hive底层执行使用的是MapReduce引擎,仍然是一个批处理过程,难以满足查询的交互性。相比之下,Impala的最大特点也是最大卖点就是它的快速。 | 查询延时上一般(秒) | |
| Kylin | Kylin采用的技术是完全预聚合的立方体,至少Kylin4之前的版本是这样的;它是把结果存到HBase,微批量的延迟;查询延迟也非常低,因为直接从HBase里面去做相应的结果查询,如果一些比较轻微的聚合可以通过HBase的Coprocessor去做一些比较轻微的一些聚合;SQL支持程度也比较完善,生产成本由于要做预聚合的立方体成本就比较高,生产成本一高的话灵活性就会变得很差,比如修改一些字段,重刷数据成本就会比较高;Join也是支持的;Kylin有一个比较好的一个事情是可以做到BitMap去重这个会是一个比较大的优势。 | 查询延时非常低(亚秒) | |
| Druid | Druid采用了一些如位图索引、字符串编码、预聚合等的技术,刚才也讲过它只预聚合最细的维度组合,这样可以防止维度爆炸,但是会牺牲一点RT(响应时间),因此做了一个权衡;支持实时;查询延迟相对Presto会低很多;SQL支持的相对完善,但是没有Presto那么完善;Druid会做一部分的预聚合,自然需要一些成本;新版本开始慢慢准备支持Join了,但还不成熟,维度表的Lookup是一直支持的;去重方式采用的是HyperLogLog,快手我看到也有第三方的contributing去支持BitMap去重,但是这个我也没有深入调研过,这边就不多说了。 | 查询延时低(亚秒) | |
| Presto | Presto采用的MPP系统和SQL On Hadoop;Presto的延时是天/小时级别,虽然现在数据湖IceBerg、HuDi比较火,他们希望把它达到分钟级别,但是就目前来看还没到很成熟大规模使用的阶段;Presto的查询延迟一般,因为它是从明细层开始查询,没有任何预聚合;SQL支持程度还是比较完善的;因为没有预聚合,数据生产成本也比较低;Join也支持的比较好;去重的话也支持普通精确去重。 | 查询延时上一般(秒) | |
| GreenPlum | Greenplum 公司开发的GP(GreenPlum)是业界最快最高性价比的关系型分布式数据库,它在开源的PG(PostgreSql)的基础上采用MPP架构(Massive Parallel Processing,海量并行处理),具有强大的大规模数据分析任务处理能力。Greenplum 是全球领先的大数据分析引擎,专为分析、机器学习和AI而打造。 | SQL支持程度非常完善 | 查询延时上一般,小查询会极大 消耗集群资源,无法实现高效并发查询 |
Doris
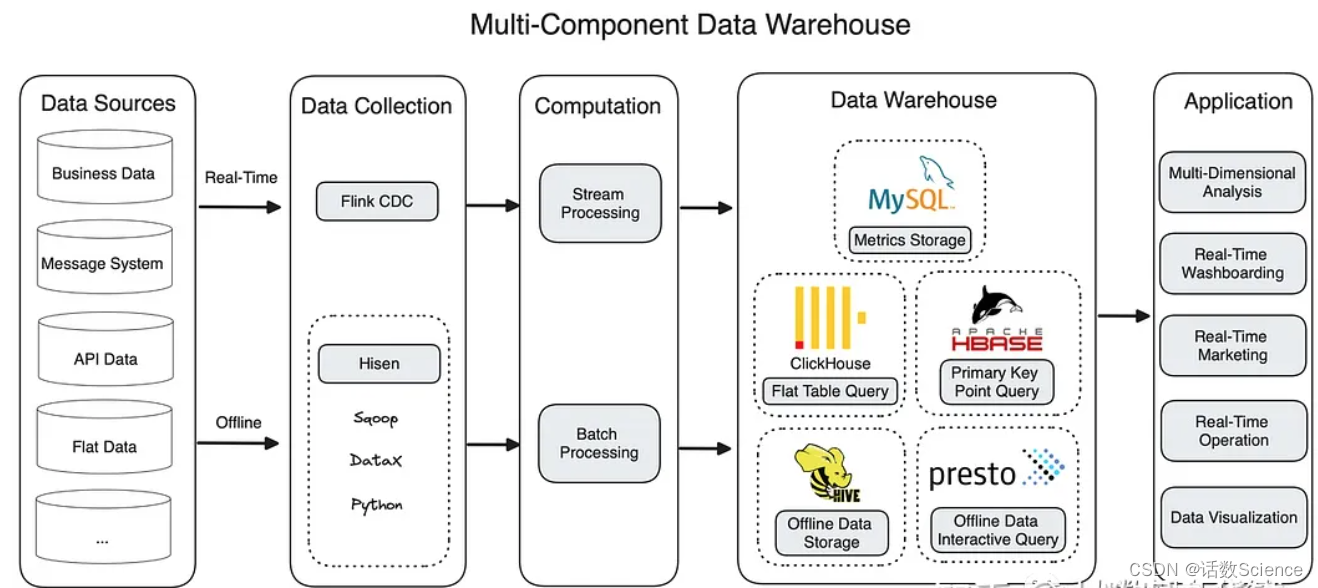
Apache Doris 能够进行实时和离线数据分析,同时支持高吞吐量的交互式分析和高并发的点查询。这就是为什么它可以取代 ClickHouse、MySQL、Presto 和 Apache HBase,作为整个数据系统的统一查询网关。

Apache Doris 可以取代 ClickHouse、MySQL、Presto 和 HBase,因为它在数据处理管道上拥有全面的功能集合。在数据摄取方面,基于对 Flink CDC 和 Merge-on-Write 的支持,实现了低延迟实时写入。通过其标签机制和事务加载来保证 Exactly-Once 写入。在数据查询方面,它同时支持星型模式和平面表聚合,因此在麻烦的多表连接和大型单表查询中都可以提供高性能。它还提供了多种方法来加速不同的查询,例如用于全文搜索和范围查询的倒排索引、用于点查询的短路计划和预备语句。
StarRocks
StarRocks开源于2021年,是OLAP引擎中名副其实的后来者,但也是时下国内最热门的开源OLAP组件之一,微信、腾讯游戏、小红书、滴滴、B站、米哈游等互联网大厂已纷纷将其引入到生产环境中,甚至担任起主力引擎的重任。
在StarRocks问世时,国内的离线、实时数仓方案其实都已经比较成熟,前面提到的几款引擎基本上主导了大厂数仓建设,由于各引擎的优势各有侧重,企业往往会采用多种引擎来适应不同的需求。
StarRocks最初主要的优势是性能,当时在单表查询方面与性能标杆ClickHouse不相上下,而join优化特性使其在多表关联查询场景下的性能表现要远远优于ClickHouse,替换ClickHouse自然也就成了StarRocks的第一个目标。
而StarRocks的野心不止于此,后来又进一步发展了联邦查询功能,成为Presto的性能升级替代方案。与此同时,StarRocks优良的预计算特性让其成为Druid的一种替代选择。
StarRocks号称新一代全场景MPP数据库,客观而言,其场景适应性确实非常强,在离线、实时分析上的表现都非常突出,很多大厂都用它实现了引擎的收敛,精简了数据架构。
这两年StarRocks一直在快速迭代,去年(2023年)推出了存算分离架构,据说最高可让存储成本下降80%。作为一款由国人主导的开源工具,阿里、腾讯、滴滴等多个互联网公司已参与到共建中,未来产品形态将如何发展,拭目以待。
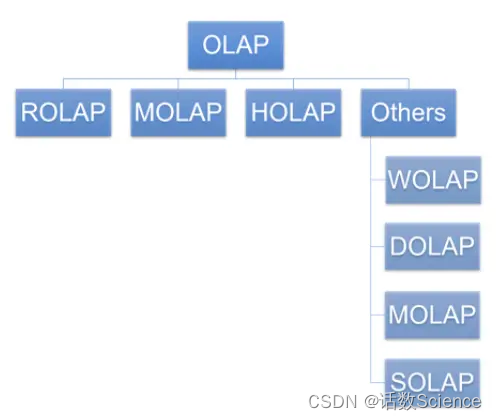
OLAP分类
OLAP 是一种让用户可以用从不同视角方便快捷的分析数据的计算方法。主流的 OLAP 可以分为3类:多维OLAP ( Multi-dimensional OLAP )、关系型OLAP ( Relational OLAP ) 和混合OLAP ( Hybrid OLAP ) 三大类。
MOLAP
MOLAP基于直接支持多维数据和操作的本机逻辑模型。数据物理上存储在多维数组中, 并且使用定位技术来访问它们。
MOLAP架构包含了数据库服务器、MOLAP服务器和前端工具三个组件。
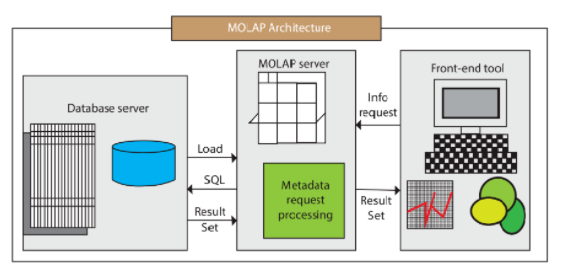
MOLAP的典型代表是:Druid 和 Kylin。MOLAP一般会根据用户定义的数据维度、度量(也可以叫指标)在数据写入时生成预聚合数据;Query查询到来时,实际上查询的是预聚合的数据而不是原始明细数据,在查询模式相对固定的场景中,这种优化提速很明显。
MOLAP 的优点和缺点都来自于其数据预处理 ( pre-processing ) 环节。数据预处理,将原始数据按照指定的计算规则预先做聚合计算,这样避免了查询过程中出现大量的即使计算,提升了查询性能。
但是这样的预聚合处理,需要预先定义维度,会限制后期数据查询的灵活性;如果查询工作涉及新的指标,需要重新增加预处理流程,损失了灵活度,存储成本也很高;同时,这种方式不支持明细数据的查询,仅适用于聚合型查询(如:sum,avg,count)。
因此,MOLAP 适用于查询场景相对固定并且对查询性能要求非常高的场景。如广告主经常使用的广告投放报表分析。
关系型OLAP ( Relational OLAP )
关系OLAP(ROLAP)是中间服务器, 它们位于关系后端服务器和用户前端工具之间,其使用关系或扩展关系DBMS来保存和处理仓库数据, 并使用OLAP中间件来提供丢失的数据。
ROLAP的体系结构如下图,其中包含了数据库服务器、ROLAP服务器和前端工具。
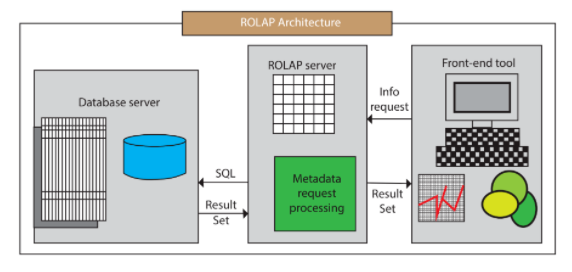
ROLAP的典型代表是:Presto,Impala,GreenPlum,Clickhouse,Elasticsearch,Hive,Spark SQL,Flink SQL。
ROLAP的优势在于以下两个方面:
第一,在数据写入时,ROLAP并未使用像MOLAP那样的预聚合技术。ROLAP收到Query请求时,会先解析Query,生成执行计划,扫描数据,执行关系型算子,在原始数据上做过滤(Where)、聚合(Sum, Avg, Count)、关联(Join),分组(Group By)、排序(Order By)等,最后将结算结果返回给用户,整个过程都是即时计算,没有预先聚合好的数据可供优化查询速度,拼的都是资源和算力的大小。
第二,ROLAP 不需要进行数据预处理 ( pre-processing ),因此查询灵活,可扩展性好。这类引擎使用 MPP 架构 ( 与Hadoop相似的大型并行处理架构,可以通过扩大并发来增加计算资源 ),可以高效处理大量数据。
但是ROLAP也存在着劣势,那就是当数据量较大或 query 较为复杂时,查询性能也无法像 MOLAP 那样稳定。所有计算都是即时触发 ( 没有预处理 ),因此会耗费更多的计算资源,带来潜在的重复计算。
因此,ROLAP 适用于对查询模式不固定、查询灵活性要求高的场景。如数据分析师常用的数据分析类产品,他们往往会对数据做各种预先不能确定的分析,所以需要更高的查询灵活性。
混合OLAP ( Hybrid OLAP )
混合 OLAP,是 MOLAP 和 ROLAP 的一种融合。当查询聚合性数据的时候,使用MOLAP 技术;当查询明细数据时,使用 ROLAP 技术。在给定使用场景的前提下,以达到查询性能的最优化。混合OLAP的技术体系架构如下图:
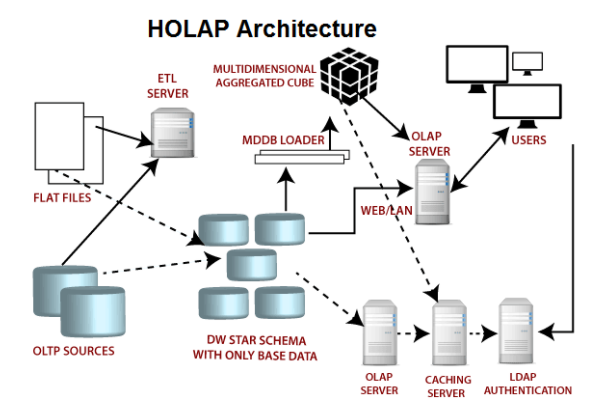
混合 OLAP的优势在于其很好的结合了MOLAP和ROLAP的优势之处,并且提供了所有聚合级别的快速访问。同时因为它仅将聚合信息存储在OLAP服务器上, 而详细记录保留在关系数据库中。因此, 不会保留详细记录的重复副本,平衡了磁盘空间需求。
混合 OLAP的劣势恰恰在于其由于集成了MOLAP和ROLAP,因此需要同时支持MOLAP和ROLAP,并且本身的体系结构也非常复杂。
Others
除此之外,还包含一些其他分类,包括启用Web的OLAP(WOLAP),桌面OLAP(DOLAP),移动OLAP(MOLAP)和空间OLAP(SOLAP)。但总体上不太流行,故此不再进行介绍。
