网站建设注意细节问题无需会员免费ppt模板

在数字化浪潮的推动下,人工智能(AI)正成为塑造未来的关键力量。硅纪元视角栏目紧跟AI科技的最新发展,捕捉行业动态;提供深入的新闻解读,助您洞悉技术背后的逻辑;汇聚行业专家的见解,分享独到的视角和思考;精选对您有价值的信息,帮助您在AI时代中把握机遇。
1 分钟速览新闻
-
微软推出VALL-E 2 模型引领零样本 TTS 新纪元
-
开源新纪元:Llama 3.1 405B 模型引领AI技术革新
-
英特尔推出AI Playground:锐炫Arc显卡的AI图像与聊天机器人新天地
-
Adobe Illustrator 和 Photoshop 新增AI 矢量图形生成等强大功能
-
AI技术点亮巴黎奥运:中国企业引领赛事革新
全球AI新闻
一、微软推出VALL-E 2 模型引领零样本 TTS 新纪元

资讯概要
微软最新发布的 VALL-E 2 模型在文本到语音(TTS)领域取得了重大突破,成为首个在合成语音稳健性、相似度和自然程度上达到人类水平的模型。VALL-E 2 展示了零样本学习能力,能够模仿不同的声音并生成逼真的语音。尽管这一技术具有巨大的潜力,微软目前仅将其作为研究项目,并未计划将其商业化。VALL-E 2 的创新之处在于其重复感知采样和分组代码建模技术,这些技术提高了模型的稳定性和效率。然而,模型的自然度和相似度仍受到语音提示的长度和质量等因素的影响。
硅纪元视角
VALL-E 2 模型的推出预示着语音合成技术的一个新时代。其零样本学习能力为个性化语音服务提供了可能,例如为残障人士提供定制化的语音合成服务,或为游戏和电影制作逼真的配音。然而,这种技术也引发了关于隐私和道德的讨论。微软的谨慎态度表明,技术进步需要与伦理和法律规范相结合,以确保其在社会中的负责任使用。此外,VALL-E 2 的创新技术,如重复感知采样和分组代码建模,为提高语音合成的稳定性和效率提供了新的解决方案,这可能对其他领域的语音处理技术产生深远影响。随着技术的不断进步,我们可以预见到语音合成技术将在教育、医疗、娱乐等多个领域发挥重要作用,为用户提供更加自然和个性化的交互体验。同时,这也为语音识别和语音处理领域的研究和开发提供了新的方向和挑战。
二、开源新纪元:Llama 3.1 405B 模型引领AI技术革新

资讯概要
Meta公司发布的Llama 3.1 405B模型,以其405亿参数的规模,成为全球最强大的开源大模型。该模型在基准测试中表现卓越,不仅超越了GPT-4 0125,还在某些领域与GPT-4o和Claude 3.5 Sonnet等闭源大模型相媲美。Llama 3.1模型包含8B、70B和405B三个尺寸版本,支持多语言和代码生成,具备复杂推理能力。Meta公司提供开放/免费的模型权重和代码,允许用户微调和部署。此外,Llama 3.1 405B模型在训练过程中采用了合成数据生成和多次迭代优化,提升了模型的泛化能力和准确性。Meta CEO扎克伯格强调,开源AI模型将推动技术平权和AI生态的繁荣发展。
硅纪元视角
Llama 3.1 405B模型的发布,标志着开源AI技术的重大突破。其在多语言支持、代码生成和复杂推理方面的优势,为AI应用的多样化场景提供了强大的支持。例如,在软件开发领域,Llama 3.1可以辅助程序员快速生成代码,提高开发效率;在多语言翻译和内容创作中,其多语言能力将极大地丰富用户体验。此外,模型的开源特性,为研究人员和开发者提供了广阔的创新空间,有助于推动AI技术的快速发展和应用落地。
从AI技术的发展趋势来看,Llama 3.1 405B模型的开源策略,有望打破闭源模型的技术壁垒,促进全球AI社区的协作与共享。这不仅有助于降低AI技术的门槛,还能激发更多创新思维的涌现。同时,开源AI模型在数据隐私和安全性方面的优势,也为用户提供了更多的选择和保障。展望未来,随着Llama 3.1模型的不断优化和功能扩展,其在图像、视频和语音等领域的应用潜力将得到进一步挖掘。开源AI技术的发展,将为各行各业带来更智能、更高效的解决方案,推动社会进入一个更加开放和创新的硅纪元。
三、英特尔推出AI Playground:锐炫Arc显卡的AI图像与聊天机器人新天地
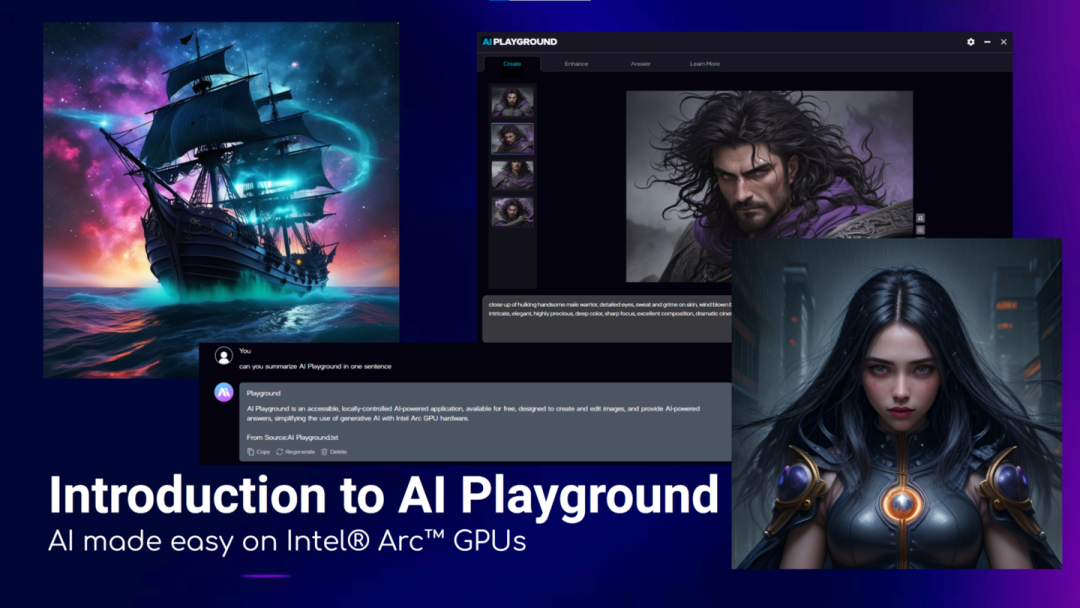
资讯概要
英特尔在7月23日正式推出了AI Playground开源软件的Beta测试版。这款软件目前支持在配备8GB或更多显存的锐炫Arc显卡的Windows电脑上运行,未来还将支持英特尔酷睿Ultra-H处理器。AI Playground是一款免费开源的AI PC入门应用程序,允许用户在本地运行AI图像生成与增强、AI聊天机器人功能。软件设计注重易用性,同时为高级用户提供了安装自定义模型和调整手动设置的能力。
硅纪元视角
AI Playground的发布标志着英特尔在AI领域迈出的重要一步,为普通用户和开发者提供了一个易于访问和使用AI技术的平台。从AI视角来看,这款软件的推出具有多方面的潜在价值。首先,AI图像生成与增强功能将极大地丰富创意产业,例如在游戏设计、影视制作等领域,设计师和艺术家可以利用AI快速生成高质量的图像内容,提高工作效率并激发创意灵感。其次,AI聊天机器人的集成为开发者提供了一个实验和开发智能对话系统的机会。这不仅可以应用于客户服务、在线教育等场景,还可以进一步推动自然语言处理和机器学习技术的发展。
此外,AI Playground支持自定义模型和手动设置的高级功能,为研究人员和高级用户提供了探索和创新AI技术的空间。这有助于推动AI技术的边界,促进新算法和应用的诞生。在具体应用场景中,AI Playground可以落地于教育领域,辅助教师设计互动式教学内容;在企业中,可以作为员工培训和技能提升的工具;在个人创作中,可以作为艺术家和设计师的辅助工具,激发创意并加速作品的创作过程。
综上所述,AI Playground的推出不仅为用户提供了一个功能丰富的AI应用平台,也为AI技术的进一步发展和应用提供了广阔的空间和可能性。随着AI技术的不断进步和普及,我们可以预见到AI Playground将在更多领域发挥重要作用,推动社会向更智能、更高效的方向发展。
四、Adobe Illustrator 和 Photoshop 新增AI矢量图形生成等强大功能

资讯概要
Adobe公司宣布旗下Illustrator和Photoshop将新增基于人工智能的功能,旨在提升设计效率与创作控制。Illustrator的“生成式形状填充”允许用户通过文字提示为形状填充矢量图形,同时支持自动生成填充内容以及从矢量或图像中识别字体。新“模型”功能则能帮助设计师将插图适配到真实物体上。Photoshop的更新包括“选区画笔工具”、“调整画笔工具”以及集成了Adobe Firefly来增强AI生成内容的能力。Adobe承诺,除非用户同意,否则不会将作品用于AI训练。
硅纪元视角
这些新功能标志着人工智能在设计领域的深度应用,极大地扩展了设计师的创作空间。通过AI辅助,设计师可以快速实现创意概念,特别是在矢量图形的即时生成和编辑上,大幅缩短了设计周期。例如,“生成式形状填充”能够根据设计师的意图智能生成图形,这为设计初期的概念验证提供了便利。而在商品设计上,“模型”功能则能帮助设计师更精准地预览设计在真实世界中的应用效果,这对于服装设计和包装设计等行业尤为重要。Photoshop的新工具则进一步简化和加速了图像编辑过程,使得设计师可以更专注于创意本身。随着AI技术的集成,设计软件正变得更加智能和高效,这不仅提高了设计师的工作效率,还可能推动整个设计行业向更高效、更个性化的方向发展。
五、中国AI技术助力巴黎奥运:赛事解说、360°直播革新体验!
资讯概要
巴黎奥运会即将盛大开幕,其背后蕴含的科技力量不容小觑。据新华社报道,阿里巴巴与英特尔等国际科技巨头将成为奥林匹克AI议程的重要合作伙伴。中国AI技术将在赛事解说、360度直播、视觉搜索等方面大放异彩,阿里巴巴通义大模型更是成为奥运首个AI大模型应用的技术提供方。此外,英特尔也在积极寻找AI应用场景,为赛事转播与管理提供技术支持。中央广播电视总台“中国红”8K转播车也已抵达法兰西体育场,准备为巴黎奥运会提供8K超高清公用信号制作,这将是夏季奥运会历史上的首次。
硅纪元视角
AI技术的融入为巴黎奥运会带来了前所未有的观赛体验。360度直播特效让观众能够全方位感受赛事的紧张刺激,黑白影像AI彩色修复技术则让历史影像焕发新生,为观众呈现更加丰富的视觉享受。碳减排辅助技术的应用体现了赛事对环境保护的重视,彰显了绿色奥运的理念。阿里巴巴通义大模型的应用,将为国际奥组委官方解说员提供强大的技术支撑,使得赛事解说更加精准、生动。AI技术在赛事解说中的应用,不仅提升了解说的专业性和观赏性,也为解说员提供了更多的创意空间。通过AI对赛事数据的实时分析和预测,解说员可以更准确地把握赛事走向,为观众提供更深入的解读。同时,AI技术还可以根据观众的反馈和偏好,实时调整解说内容和风格,实现个性化的观赛体验。
在赛事转播和管理方面,AI技术的应用大大提高了赛事的智能化水平。AI算法可以对赛事进行实时监控和分析,及时发现并处理各种异常情况,确保赛事的顺利进行。此外,AI技术还可以对赛事数据进行深度挖掘,为赛事组织者提供决策支持,优化赛事安排和资源配置。
8K超高清技术的应用,将为观众带来前所未有的视觉震撼。8K画质的细腻度和色彩表现力远超传统高清技术,能够呈现出更加真实、生动的赛事画面。这不仅提升了观众的观赛体验,也为体育赛事的传播和推广提供了新的可能。
总体来看,AI技术在巴黎奥运会的广泛应用,不仅提升了赛事的专业性和观赏性,也为体育赛事的智能化、个性化发展提供了新的思路和方向。随着AI技术的不断进步和创新,未来的体育赛事将更加精彩纷呈,为全球观众带来更加丰富、多元的观赛体验。
