营销型国外网站个人简历范文
经常听到有朋友说,学习编程是一件非常枯燥无味的事情。其实,大家有没有认真想过,可能是我们的学习方法不对?
比方说,你有没有想过,可以通过打游戏来学编程?
今天我想跟大家分享几个Python小游戏,教你如何通过边打游戏边学编程!
1、吃金币
源码分享:
import os
import cfg
import sys
import pygame
import random
from modules import *'''游戏初始化'''
def initGame():# 初始化pygame, 设置展示窗口pygame.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('catch coins —— 九歌')# 加载必要的游戏素材game_images = {}for key, value in cfg.IMAGE_PATHS.items():if isinstance(value, list):images = []for item in value: images.append(pygame.image.load(item))game_images[key] = imageselse:game_images[key] = pygame.image.load(value)game_sounds = {}for key, value in cfg.AUDIO_PATHS.items():if key == 'bgm': continuegame_sounds[key] = pygame.mixer.Sound(value)# 返回初始化数据return screen, game_images, game_sounds'''主函数'''
def main():# 初始化screen, game_images, game_sounds = initGame()# 播放背景音乐pygame.mixer.music.load(cfg.AUDIO_PATHS['bgm'])pygame.mixer.music.play(-1, 0.0)# 字体加载font = pygame.font.Font(cfg.FONT_PATH, 40)# 定义herohero = Hero(game_images['hero'], position=(375, 520))# 定义食物组food_sprites_group = pygame.sprite.Group()generate_food_freq = random.randint(10, 20)generate_food_count = 0# 当前分数/历史最高分score = 0highest_score = 0 if not os.path.exists(cfg.HIGHEST_SCORE_RECORD_FILEPATH) else int(open(cfg.HIGHEST_SCORE_RECORD_FILEPATH).read())# 游戏主循环clock = pygame.time.Clock()while True:# --填充背景screen.fill(0)screen.blit(game_images['background'], (0, 0))# --倒计时信息countdown_text = 'Count down: ' + str((90000 - pygame.time.get_ticks()) // 60000) + ":" + str((90000 - pygame.time.get_ticks()) // 1000 % 60).zfill(2)countdown_text = font.render(countdown_text, True, (0, 0, 0))countdown_rect = countdown_text.get_rect()countdown_rect.topright = [cfg.SCREENSIZE[0]-30, 5]screen.blit(countdown_text, countdown_rect)# --按键检测for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()key_pressed = pygame.key.get_pressed()if key_pressed[pygame.K_a] or key_pressed[pygame.K_LEFT]:hero.move(cfg.SCREENSIZE, 'left')if key_pressed[pygame.K_d] or key_pressed[pygame.K_RIGHT]:hero.move(cfg.SCREENSIZE, 'right')# --随机生成食物generate_food_count += 1if generate_food_count > generate_food_freq:generate_food_freq = random.randint(10, 20)generate_food_count = 0food = Food(game_images, random.choice(['gold',] * 10 + ['apple']), cfg.SCREENSIZE)food_sprites_group.add(food)# --更新食物for food in food_sprites_group:if food.update(): food_sprites_group.remove(food)# --碰撞检测for food in food_sprites_group:if pygame.sprite.collide_mask(food, hero):game_sounds['get'].play()food_sprites_group.remove(food)score += food.scoreif score > highest_score: highest_score = score# --画herohero.draw(screen)# --画食物food_sprites_group.draw(screen)# --显示得分score_text = f'Score: {score}, Highest: {highest_score}'score_text = font.render(score_text, True, (0, 0, 0))score_rect = score_text.get_rect()score_rect.topleft = [5, 5]screen.blit(score_text, score_rect)# --判断游戏是否结束if pygame.time.get_ticks() >= 90000:break# --更新屏幕pygame.display.flip()clock.tick(cfg.FPS)# 游戏结束, 记录最高分并显示游戏结束画面fp = open(cfg.HIGHEST_SCORE_RECORD_FILEPATH, 'w')fp.write(str(highest_score))fp.close()return showEndGameInterface(screen, cfg, score, highest_score)'''run'''
if __name__ == '__main__':while main():pass
技术提升
技术要学会分享、交流,不建议闭门造车。一个人走的很快、一堆人可以走的更远。
好的技术文章离不开粉丝的分享、推荐,资料干货、资料分享、数据、技术交流提升,均可加交流群获取,群友已超过2000人,添加时切记的备注方式为:来源+兴趣方向,方便找到志同道合的朋友。
方式①、添加微信号:pythoner666,备注:来自 CSDN + python
方式②、微信搜索公众号:Python学习与数据挖掘,后台回复:加群
2、打乒乓
源码分享:
import sys
import cfg
import pygame
from modules import *'''定义按钮'''
def Button(screen, position, text, button_size=(200, 50)):left, top = positionbwidth, bheight = button_sizepygame.draw.line(screen, (150, 150, 150), (left, top), (left+bwidth, top), 5)pygame.draw.line(screen, (150, 150, 150), (left, top-2), (left, top+bheight), 5)pygame.draw.line(screen, (50, 50, 50), (left, top+bheight), (left+bwidth, top+bheight), 5)pygame.draw.line(screen, (50, 50, 50), (left+bwidth, top+bheight), (left+bwidth, top), 5)pygame.draw.rect(screen, (100, 100, 100), (left, top, bwidth, bheight))font = pygame.font.Font(cfg.FONTPATH, 30)text_render = font.render(text, 1, (255, 235, 205))return screen.blit(text_render, (left+50, top+10))'''
Function:开始界面
Input:--screen: 游戏界面
Return:--game_mode: 1(单人模式)/2(双人模式)
'''
def startInterface(screen):clock = pygame.time.Clock()while True:screen.fill((41, 36, 33))button_1 = Button(screen, (150, 175), '1 Player')button_2 = Button(screen, (150, 275), '2 Player')for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()if event.type == pygame.MOUSEBUTTONDOWN:if button_1.collidepoint(pygame.mouse.get_pos()):return 1elif button_2.collidepoint(pygame.mouse.get_pos()):return 2clock.tick(10)pygame.display.update()'''结束界面'''
def endInterface(screen, score_left, score_right):clock = pygame.time.Clock()font1 = pygame.font.Font(cfg.FONTPATH, 30)font2 = pygame.font.Font(cfg.FONTPATH, 20)msg = 'Player on left won!' if score_left > score_right else 'Player on right won!'texts = [font1.render(msg, True, cfg.WHITE),font2.render('Press ESCAPE to quit.', True, cfg.WHITE),font2.render('Press ENTER to continue or play again.', True, cfg.WHITE)]positions = [[120, 200], [155, 270], [80, 300]]while True:screen.fill((41, 36, 33))for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()if event.type == pygame.KEYDOWN:if event.key == pygame.K_RETURN:returnelif event.key == pygame.K_ESCAPE:sys.exit()pygame.quit()for text, pos in zip(texts, positions):screen.blit(text, pos)clock.tick(10)pygame.display.update()'''运行游戏Demo'''
def runDemo(screen):# 加载游戏素材hit_sound = pygame.mixer.Sound(cfg.HITSOUNDPATH)goal_sound = pygame.mixer.Sound(cfg.GOALSOUNDPATH)pygame.mixer.music.load(cfg.BGMPATH)pygame.mixer.music.play(-1, 0.0)font = pygame.font.Font(cfg.FONTPATH, 50)# 开始界面game_mode = startInterface(screen)# 游戏主循环# --左边球拍(ws控制, 仅双人模式时可控制)score_left = 0racket_left = Racket(cfg.RACKETPICPATH, 'LEFT', cfg)# --右边球拍(↑↓控制)score_right = 0racket_right = Racket(cfg.RACKETPICPATH, 'RIGHT', cfg)# --球ball = Ball(cfg.BALLPICPATH, cfg)clock = pygame.time.Clock()while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit(-1)screen.fill((41, 36, 33))# 玩家操作pressed_keys = pygame.key.get_pressed()if pressed_keys[pygame.K_UP]:racket_right.move('UP')elif pressed_keys[pygame.K_DOWN]:racket_right.move('DOWN')if game_mode == 2:if pressed_keys[pygame.K_w]:racket_left.move('UP')elif pressed_keys[pygame.K_s]:racket_left.move('DOWN')else:racket_left.automove(ball)# 球运动scores = ball.move(ball, racket_left, racket_right, hit_sound, goal_sound)score_left += scores[0]score_right += scores[1]# 显示# --分隔线pygame.draw.rect(screen, cfg.WHITE, (247, 0, 6, 500))# --球ball.draw(screen)# --拍racket_left.draw(screen)racket_right.draw(screen)# --得分screen.blit(font.render(str(score_left), False, cfg.WHITE), (150, 10))screen.blit(font.render(str(score_right), False, cfg.WHITE), (300, 10))if score_left == 11 or score_right == 11:return score_left, score_rightclock.tick(100)pygame.display.update()'''主函数'''
def main():# 初始化pygame.init()pygame.mixer.init()screen = pygame.display.set_mode((cfg.WIDTH, cfg.HEIGHT))pygame.display.set_caption('pingpong —— 九歌')# 开始游戏while True:score_left, score_right = runDemo(screen)endInterface(screen, score_left, score_right)'''run'''
if __name__ == '__main__':main()3、滑雪
源码分享:
import sys
import cfg
import pygame
import random'''滑雪者类'''
class SkierClass(pygame.sprite.Sprite):def __init__(self):pygame.sprite.Sprite.__init__(self)# 滑雪者的朝向(-2到2)self.direction = 0self.imagepaths = cfg.SKIER_IMAGE_PATHS[:-1]self.image = pygame.image.load(self.imagepaths[self.direction])self.rect = self.image.get_rect()self.rect.center = [320, 100]self.speed = [self.direction, 6-abs(self.direction)*2]'''改变滑雪者的朝向. 负数为向左,正数为向右,0为向前'''def turn(self, num):self.direction += numself.direction = max(-2, self.direction)self.direction = min(2, self.direction)center = self.rect.centerself.image = pygame.image.load(self.imagepaths[self.direction])self.rect = self.image.get_rect()self.rect.center = centerself.speed = [self.direction, 6-abs(self.direction)*2]return self.speed'''移动滑雪者'''def move(self):self.rect.centerx += self.speed[0]self.rect.centerx = max(20, self.rect.centerx)self.rect.centerx = min(620, self.rect.centerx)'''设置为摔倒状态'''def setFall(self):self.image = pygame.image.load(cfg.SKIER_IMAGE_PATHS[-1])'''设置为站立状态'''def setForward(self):self.direction = 0self.image = pygame.image.load(self.imagepaths[self.direction])'''
Function:障碍物类
Input:img_path: 障碍物图片路径location: 障碍物位置attribute: 障碍物类别属性
'''
class ObstacleClass(pygame.sprite.Sprite):def __init__(self, img_path, location, attribute):pygame.sprite.Sprite.__init__(self)self.img_path = img_pathself.image = pygame.image.load(self.img_path)self.location = locationself.rect = self.image.get_rect()self.rect.center = self.locationself.attribute = attributeself.passed = False'''移动'''def move(self, num):self.rect.centery = self.location[1] - num'''创建障碍物'''
def createObstacles(s, e, num=10):obstacles = pygame.sprite.Group()locations = []for i in range(num):row = random.randint(s, e)col = random.randint(0, 9)location = [col*64+20, row*64+20]if location not in locations:locations.append(location)attribute = random.choice(list(cfg.OBSTACLE_PATHS.keys()))img_path = cfg.OBSTACLE_PATHS[attribute]obstacle = ObstacleClass(img_path, location, attribute)obstacles.add(obstacle)return obstacles'''合并障碍物'''
def AddObstacles(obstacles0, obstacles1):obstacles = pygame.sprite.Group()for obstacle in obstacles0:obstacles.add(obstacle)for obstacle in obstacles1:obstacles.add(obstacle)return obstacles'''显示游戏开始界面'''
def ShowStartInterface(screen, screensize):screen.fill((255, 255, 255))tfont = pygame.font.Font(cfg.FONTPATH, screensize[0]//5)cfont = pygame.font.Font(cfg.FONTPATH, screensize[0]//20)title = tfont.render(u'滑雪游戏', True, (255, 0, 0))content = cfont.render(u'按任意键开始游戏', True, (0, 0, 255))trect = title.get_rect()trect.midtop = (screensize[0]/2, screensize[1]/5)crect = content.get_rect()crect.midtop = (screensize[0]/2, screensize[1]/2)screen.blit(title, trect)screen.blit(content, crect)while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()elif event.type == pygame.KEYDOWN:returnpygame.display.update()'''显示分数'''
def showScore(screen, score, pos=(10, 10)):font = pygame.font.Font(cfg.FONTPATH, 30)score_text = font.render("Score: %s" % score, True, (0, 0, 0))screen.blit(score_text, pos)'''更新当前帧的游戏画面'''
def updateFrame(screen, obstacles, skier, score):screen.fill((255, 255, 255))obstacles.draw(screen)screen.blit(skier.image, skier.rect)showScore(screen, score)pygame.display.update()'''主程序'''
def main():# 游戏初始化pygame.init()pygame.mixer.init()pygame.mixer.music.load(cfg.BGMPATH)pygame.mixer.music.set_volume(0.4)pygame.mixer.music.play(-1)# 设置屏幕screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('滑雪游戏 —— 九歌')# 游戏开始界面ShowStartInterface(screen, cfg.SCREENSIZE)# 实例化游戏精灵# --滑雪者skier = SkierClass()# --创建障碍物obstacles0 = createObstacles(20, 29)obstacles1 = createObstacles(10, 19)obstaclesflag = 0obstacles = AddObstacles(obstacles0, obstacles1)# 游戏clockclock = pygame.time.Clock()# 记录滑雪的距离distance = 0# 记录当前的分数score = 0# 记录当前的速度speed = [0, 6]# 游戏主循环while True:# --事件捕获for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()if event.type == pygame.KEYDOWN:if event.key == pygame.K_LEFT or event.key == pygame.K_a:speed = skier.turn(-1)elif event.key == pygame.K_RIGHT or event.key == pygame.K_d:speed = skier.turn(1)# --更新当前游戏帧的数据skier.move()distance += speed[1]if distance >= 640 and obstaclesflag == 0:obstaclesflag = 1obstacles0 = createObstacles(20, 29)obstacles = AddObstacles(obstacles0, obstacles1)if distance >= 1280 and obstaclesflag == 1:obstaclesflag = 0distance -= 1280for obstacle in obstacles0:obstacle.location[1] = obstacle.location[1] - 1280obstacles1 = createObstacles(10, 19)obstacles = AddObstacles(obstacles0, obstacles1)for obstacle in obstacles:obstacle.move(distance)# --碰撞检测hitted_obstacles = pygame.sprite.spritecollide(skier, obstacles, False)if hitted_obstacles:if hitted_obstacles[0].attribute == "tree" and not hitted_obstacles[0].passed:score -= 50skier.setFall()updateFrame(screen, obstacles, skier, score)pygame.time.delay(1000)skier.setForward()speed = [0, 6]hitted_obstacles[0].passed = Trueelif hitted_obstacles[0].attribute == "flag" and not hitted_obstacles[0].passed:score += 10obstacles.remove(hitted_obstacles[0])# --更新屏幕updateFrame(screen, obstacles, skier, score)clock.tick(cfg.FPS)'''run'''
if __name__ == '__main__':main();4、并夕夕版飞机大战
源码分享:
import sys
import cfg
import pygame
from modules import *'''游戏界面'''
def GamingInterface(num_player, screen):# 初始化pygame.mixer.music.load(cfg.SOUNDPATHS['Cool Space Music'])pygame.mixer.music.set_volume(0.4)pygame.mixer.music.play(-1)explosion_sound = pygame.mixer.Sound(cfg.SOUNDPATHS['boom'])fire_sound = pygame.mixer.Sound(cfg.SOUNDPATHS['shot'])font = pygame.font.Font(cfg.FONTPATH, 20)# 游戏背景图bg_imgs = [cfg.IMAGEPATHS['bg_big'], cfg.IMAGEPATHS['seamless_space'], cfg.IMAGEPATHS['space3']]bg_move_dis = 0bg_1 = pygame.image.load(bg_imgs[0]).convert()bg_2 = pygame.image.load(bg_imgs[1]).convert()bg_3 = pygame.image.load(bg_imgs[2]).convert()# 玩家, 子弹和小行星精灵组player_group = pygame.sprite.Group()bullet_group = pygame.sprite.Group()asteroid_group = pygame.sprite.Group()# 产生小行星的时间间隔asteroid_ticks = 90for i in range(num_player):player_group.add(Ship(i+1, cfg))clock = pygame.time.Clock()# 分数score_1, score_2 = 0, 0# 游戏主循环while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()# --玩家一: ↑↓←→控制, j射击; 玩家二: wsad控制, 空格射击pressed_keys = pygame.key.get_pressed()for idx, player in enumerate(player_group):direction = Noneif idx == 0:if pressed_keys[pygame.K_UP]:direction = 'up'elif pressed_keys[pygame.K_DOWN]:direction = 'down'elif pressed_keys[pygame.K_LEFT]:direction = 'left'elif pressed_keys[pygame.K_RIGHT]:direction = 'right'if direction:player.move(direction)if pressed_keys[pygame.K_j]:if player.cooling_time == 0:fire_sound.play()bullet_group.add(player.shot())player.cooling_time = 20elif idx == 1:if pressed_keys[pygame.K_w]:direction = 'up'elif pressed_keys[pygame.K_s]:direction = 'down'elif pressed_keys[pygame.K_a]:direction = 'left'elif pressed_keys[pygame.K_d]:direction = 'right'if direction:player.move(direction)if pressed_keys[pygame.K_SPACE]:if player.cooling_time == 0:fire_sound.play()bullet_group.add(player.shot())player.cooling_time = 20if player.cooling_time > 0:player.cooling_time -= 1if (score_1 + score_2) < 500:background = bg_1elif (score_1 + score_2) < 1500:background = bg_2else:background = bg_3# --向下移动背景图实现飞船向上移动的效果screen.blit(background, (0, -background.get_rect().height + bg_move_dis))screen.blit(background, (0, bg_move_dis))bg_move_dis = (bg_move_dis + 2) % background.get_rect().height# --生成小行星if asteroid_ticks == 0:asteroid_ticks = 90asteroid_group.add(Asteroid(cfg))else:asteroid_ticks -= 1# --画飞船for player in player_group:if pygame.sprite.spritecollide(player, asteroid_group, True, None):player.explode_step = 1explosion_sound.play()elif player.explode_step > 0:if player.explode_step > 3:player_group.remove(player)if len(player_group) == 0:returnelse:player.explode(screen)else:player.draw(screen)# --画子弹for bullet in bullet_group:bullet.move()if pygame.sprite.spritecollide(bullet, asteroid_group, True, None):bullet_group.remove(bullet)if bullet.player_idx == 1:score_1 += 1else:score_2 += 1else:bullet.draw(screen)# --画小行星for asteroid in asteroid_group:asteroid.move()asteroid.rotate()asteroid.draw(screen)# --显示分数score_1_text = '玩家一得分: %s' % score_1score_2_text = '玩家二得分: %s' % score_2text_1 = font.render(score_1_text, True, (0, 0, 255))text_2 = font.render(score_2_text, True, (255, 0, 0))screen.blit(text_1, (2, 5))screen.blit(text_2, (2, 35))# --屏幕刷新pygame.display.update()clock.tick(60)'''主函数'''
def main():pygame.init()pygame.font.init()pygame.mixer.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('飞机大战 —— 九歌')num_player = StartInterface(screen, cfg)if num_player == 1:while True:GamingInterface(num_player=1, screen=screen)EndInterface(screen, cfg)else:while True:GamingInterface(num_player=2, screen=screen)EndInterface(screen, cfg)'''run'''
if __name__ == '__main__':main()5、打地鼠
源码分享:
import cfg
import sys
import pygame
import random
from modules import *'''游戏初始化'''
def initGame():pygame.init()pygame.mixer.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('打地鼠 —— 九歌')return screen'''主函数'''
def main():# 初始化screen = initGame()# 加载背景音乐和其他音效pygame.mixer.music.load(cfg.BGM_PATH)pygame.mixer.music.play(-1)audios = {'count_down': pygame.mixer.Sound(cfg.COUNT_DOWN_SOUND_PATH),'hammering': pygame.mixer.Sound(cfg.HAMMERING_SOUND_PATH)}# 加载字体font = pygame.font.Font(cfg.FONT_PATH, 40)# 加载背景图片bg_img = pygame.image.load(cfg.GAME_BG_IMAGEPATH)# 开始界面startInterface(screen, cfg.GAME_BEGIN_IMAGEPATHS)# 地鼠改变位置的计时hole_pos = random.choice(cfg.HOLE_POSITIONS)change_hole_event = pygame.USEREVENTpygame.time.set_timer(change_hole_event, 800)# 地鼠mole = Mole(cfg.MOLE_IMAGEPATHS, hole_pos)# 锤子hammer = Hammer(cfg.HAMMER_IMAGEPATHS, (500, 250))# 时钟clock = pygame.time.Clock()# 分数your_score = 0flag = False# 初始时间init_time = pygame.time.get_ticks()# 游戏主循环while True:# --游戏时间为60stime_remain = round((61000 - (pygame.time.get_ticks() - init_time)) / 1000.)# --游戏时间减少, 地鼠变位置速度变快if time_remain == 40 and not flag:hole_pos = random.choice(cfg.HOLE_POSITIONS)mole.reset()mole.setPosition(hole_pos)pygame.time.set_timer(change_hole_event, 650)flag = Trueelif time_remain == 20 and flag:hole_pos = random.choice(cfg.HOLE_POSITIONS)mole.reset()mole.setPosition(hole_pos)pygame.time.set_timer(change_hole_event, 500)flag = False# --倒计时音效if time_remain == 10:audios['count_down'].play()# --游戏结束if time_remain < 0: breakcount_down_text = font.render('Time: '+str(time_remain), True, cfg.WHITE)# --按键检测for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()elif event.type == pygame.MOUSEMOTION:hammer.setPosition(pygame.mouse.get_pos())elif event.type == pygame.MOUSEBUTTONDOWN:if event.button == 1:hammer.setHammering()elif event.type == change_hole_event:hole_pos = random.choice(cfg.HOLE_POSITIONS)mole.reset()mole.setPosition(hole_pos)# --碰撞检测if hammer.is_hammering and not mole.is_hammer:is_hammer = pygame.sprite.collide_mask(hammer, mole)if is_hammer:audios['hammering'].play()mole.setBeHammered()your_score += 10# --分数your_score_text = font.render('Score: '+str(your_score), True, cfg.BROWN)# --绑定必要的游戏元素到屏幕(注意顺序)screen.blit(bg_img, (0, 0))screen.blit(count_down_text, (875, 8))screen.blit(your_score_text, (800, 430))mole.draw(screen)hammer.draw(screen)# --更新pygame.display.flip()clock.tick(60)# 读取最佳分数(try块避免第一次游戏无.rec文件)try:best_score = int(open(cfg.RECORD_PATH).read())except:best_score = 0# 若当前分数大于最佳分数则更新最佳分数if your_score > best_score:f = open(cfg.RECORD_PATH, 'w')f.write(str(your_score))f.close()# 结束界面score_info = {'your_score': your_score, 'best_score': best_score}is_restart = endInterface(screen, cfg.GAME_END_IMAGEPATH, cfg.GAME_AGAIN_IMAGEPATHS, score_info, cfg.FONT_PATH, [cfg.WHITE, cfg.RED], cfg.SCREENSIZE)return is_restart'''run'''
if __name__ == '__main__':while True:is_restart = main()if not is_restart:break6、小恐龙
玩法:上下控制起跳躲避
源码分享:
import cfg
import sys
import random
import pygame
from modules import *'''main'''
def main(highest_score):# 游戏初始化pygame.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('九歌')# 导入所有声音文件sounds = {}for key, value in cfg.AUDIO_PATHS.items():sounds[key] = pygame.mixer.Sound(value)# 游戏开始界面GameStartInterface(screen, sounds, cfg)# 定义一些游戏中必要的元素和变量score = 0score_board = Scoreboard(cfg.IMAGE_PATHS['numbers'], position=(534, 15), bg_color=cfg.BACKGROUND_COLOR)highest_score = highest_scorehighest_score_board = Scoreboard(cfg.IMAGE_PATHS['numbers'], position=(435, 15), bg_color=cfg.BACKGROUND_COLOR, is_highest=True)dino = Dinosaur(cfg.IMAGE_PATHS['dino'])ground = Ground(cfg.IMAGE_PATHS['ground'], position=(0, cfg.SCREENSIZE[1]))cloud_sprites_group = pygame.sprite.Group()cactus_sprites_group = pygame.sprite.Group()ptera_sprites_group = pygame.sprite.Group()add_obstacle_timer = 0score_timer = 0# 游戏主循环clock = pygame.time.Clock()while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()elif event.type == pygame.KEYDOWN:if event.key == pygame.K_SPACE or event.key == pygame.K_UP:dino.jump(sounds)elif event.key == pygame.K_DOWN:dino.duck()elif event.type == pygame.KEYUP and event.key == pygame.K_DOWN:dino.unduck()screen.fill(cfg.BACKGROUND_COLOR)# --随机添加云if len(cloud_sprites_group) < 5 and random.randrange(0, 300) == 10:cloud_sprites_group.add(Cloud(cfg.IMAGE_PATHS['cloud'], position=(cfg.SCREENSIZE[0], random.randrange(30, 75))))# --随机添加仙人掌/飞龙add_obstacle_timer += 1if add_obstacle_timer > random.randrange(50, 150):add_obstacle_timer = 0random_value = random.randrange(0, 10)if random_value >= 5 and random_value <= 7:cactus_sprites_group.add(Cactus(cfg.IMAGE_PATHS['cacti']))else:position_ys = [cfg.SCREENSIZE[1]*0.82, cfg.SCREENSIZE[1]*0.75, cfg.SCREENSIZE[1]*0.60, cfg.SCREENSIZE[1]*0.20]ptera_sprites_group.add(Ptera(cfg.IMAGE_PATHS['ptera'], position=(600, random.choice(position_ys))))# --更新游戏元素dino.update()ground.update()cloud_sprites_group.update()cactus_sprites_group.update()ptera_sprites_group.update()score_timer += 1if score_timer > (cfg.FPS//12):score_timer = 0score += 1score = min(score, 99999)if score > highest_score:highest_score = scoreif score % 100 == 0:sounds['point'].play()if score % 1000 == 0:ground.speed -= 1for item in cloud_sprites_group:item.speed -= 1for item in cactus_sprites_group:item.speed -= 1for item in ptera_sprites_group:item.speed -= 1# --碰撞检测for item in cactus_sprites_group:if pygame.sprite.collide_mask(dino, item):dino.die(sounds)for item in ptera_sprites_group:if pygame.sprite.collide_mask(dino, item):dino.die(sounds)# --将游戏元素画到屏幕上dino.draw(screen)ground.draw(screen)cloud_sprites_group.draw(screen)cactus_sprites_group.draw(screen)ptera_sprites_group.draw(screen)score_board.set(score)highest_score_board.set(highest_score)score_board.draw(screen)highest_score_board.draw(screen)# --更新屏幕pygame.display.update()clock.tick(cfg.FPS)# --游戏是否结束if dino.is_dead:break# 游戏结束界面return GameEndInterface(screen, cfg), highest_score'''run'''
if __name__ == '__main__':highest_score = 0while True:flag, highest_score = main(highest_score)if not flag: break
7、消消乐
玩法:三个相连就能消除
源码分享:
import os
import sys
import cfg
import pygame
from modules import *'''游戏主程序'''
def main():pygame.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('Gemgem —— 九歌')# 加载背景音乐pygame.mixer.init()pygame.mixer.music.load(os.path.join(cfg.ROOTDIR, "resources/audios/bg.mp3"))pygame.mixer.music.set_volume(0.6)pygame.mixer.music.play(-1)# 加载音效sounds = {}sounds['mismatch'] = pygame.mixer.Sound(os.path.join(cfg.ROOTDIR, 'resources/audios/badswap.wav'))sounds['match'] = []for i in range(6):sounds['match'].append(pygame.mixer.Sound(os.path.join(cfg.ROOTDIR, 'resources/audios/match%s.wav' % i)))# 加载字体font = pygame.font.Font(os.path.join(cfg.ROOTDIR, 'resources/font/font.TTF'), 25)# 图片加载gem_imgs = []for i in range(1, 8):gem_imgs.append(os.path.join(cfg.ROOTDIR, 'resources/images/gem%s.png' % i))# 主循环game = gemGame(screen, sounds, font, gem_imgs, cfg)while True:score = game.start()flag = False# 一轮游戏结束后玩家选择重玩或者退出while True:for event in pygame.event.get():if event.type == pygame.QUIT or (event.type == pygame.KEYUP and event.key == pygame.K_ESCAPE):pygame.quit()sys.exit()elif event.type == pygame.KEYUP and event.key == pygame.K_r:flag = Trueif flag:breakscreen.fill((135, 206, 235))text0 = 'Final score: %s' % scoretext1 = 'Press <R> to restart the game.'text2 = 'Press <Esc> to quit the game.'y = 150for idx, text in enumerate([text0, text1, text2]):text_render = font.render(text, 1, (85, 65, 0))rect = text_render.get_rect()if idx == 0:rect.left, rect.top = (212, y)elif idx == 1:rect.left, rect.top = (122.5, y)else:rect.left, rect.top = (126.5, y)y += 100screen.blit(text_render, rect)pygame.display.update()game.reset()'''run'''
if __name__ == '__main__':main()8、俄罗斯方块
玩法:童年经典,普通模式没啥意思,小时候我们都是玩加速的。
源码分享:
import os
import sys
import random
from modules import *
from PyQt5.QtGui import *
from PyQt5.QtCore import *
from PyQt5.QtWidgets import *'''定义俄罗斯方块游戏类'''
class TetrisGame(QMainWindow):def __init__(self, parent=None):super(TetrisGame, self).__init__(parent)# 是否暂停ingself.is_paused = False# 是否开始ingself.is_started = Falseself.initUI()'''界面初始化'''def initUI(self):# iconself.setWindowIcon(QIcon(os.path.join(os.getcwd(), 'resources/icon.jpg')))# 块大小self.grid_size = 22# 游戏帧率self.fps = 200self.timer = QBasicTimer()# 焦点self.setFocusPolicy(Qt.StrongFocus)# 水平布局layout_horizontal = QHBoxLayout()self.inner_board = InnerBoard()self.external_board = ExternalBoard(self, self.grid_size, self.inner_board)layout_horizontal.addWidget(self.external_board)self.side_panel = SidePanel(self, self.grid_size, self.inner_board)layout_horizontal.addWidget(self.side_panel)self.status_bar = self.statusBar()self.external_board.score_signal[str].connect(self.status_bar.showMessage)self.start()self.center()self.setWindowTitle('Tetris —— 九歌')self.show()self.setFixedSize(self.external_board.width() + self.side_panel.width(), self.side_panel.height() + self.status_bar.height())'''游戏界面移动到屏幕中间'''def center(self):screen = QDesktopWidget().screenGeometry()size = self.geometry()self.move((screen.width() - size.width()) // 2, (screen.height() - size.height()) // 2)'''更新界面'''def updateWindow(self):self.external_board.updateData()self.side_panel.updateData()self.update()'''开始'''def start(self):if self.is_started:returnself.is_started = Trueself.inner_board.createNewTetris()self.timer.start(self.fps, self)'''暂停/不暂停'''def pause(self):if not self.is_started:returnself.is_paused = not self.is_pausedif self.is_paused:self.timer.stop()self.external_board.score_signal.emit('Paused')else:self.timer.start(self.fps, self)self.updateWindow()'''计时器事件'''def timerEvent(self, event):if event.timerId() == self.timer.timerId():removed_lines = self.inner_board.moveDown()self.external_board.score += removed_linesself.updateWindow()else:super(TetrisGame, self).timerEvent(event)'''按键事件'''def keyPressEvent(self, event):if not self.is_started or self.inner_board.current_tetris == tetrisShape().shape_empty:super(TetrisGame, self).keyPressEvent(event)returnkey = event.key()# P键暂停if key == Qt.Key_P:self.pause()returnif self.is_paused:return# 向左elif key == Qt.Key_Left:self.inner_board.moveLeft()# 向右elif key == Qt.Key_Right:self.inner_board.moveRight()# 旋转elif key == Qt.Key_Up:self.inner_board.rotateAnticlockwise()# 快速坠落elif key == Qt.Key_Space:self.external_board.score += self.inner_board.dropDown()else:super(TetrisGame, self).keyPressEvent(event)self.updateWindow()'''run'''
if __name__ == '__main__':app = QApplication([])tetris = TetrisGame()sys.exit(app.exec_())
9、贪吃蛇
玩法:童年经典,普通魔术也没啥意思,小时候玩的也是加速的。
源码分享:
import cfg
import sys
import pygame
from modules import *'''主函数'''
def main(cfg):# 游戏初始化pygame.init()screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.display.set_caption('Greedy Snake —— 九歌')clock = pygame.time.Clock()# 播放背景音乐pygame.mixer.music.load(cfg.BGMPATH)pygame.mixer.music.play(-1)# 游戏主循环snake = Snake(cfg)apple = Apple(cfg, snake.coords)score = 0while True:screen.fill(cfg.BLACK)# --按键检测for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()elif event.type == pygame.KEYDOWN:if event.key in [pygame.K_UP, pygame.K_DOWN, pygame.K_LEFT, pygame.K_RIGHT]:snake.setDirection({pygame.K_UP: 'up', pygame.K_DOWN: 'down', pygame.K_LEFT: 'left', pygame.K_RIGHT: 'right'}[event.key])# --更新贪吃蛇和食物if snake.update(apple):apple = Apple(cfg, snake.coords)score += 1# --判断游戏是否结束if snake.isgameover: break# --显示游戏里必要的元素drawGameGrid(cfg, screen)snake.draw(screen)apple.draw(screen)showScore(cfg, score, screen)# --屏幕更新pygame.display.update()clock.tick(cfg.FPS)return endInterface(screen, cfg)'''run'''
if __name__ == '__main__':while True:if not main(cfg):break
10、24点小游戏
玩法:通过加减乘除操作,小学生都没问题的。
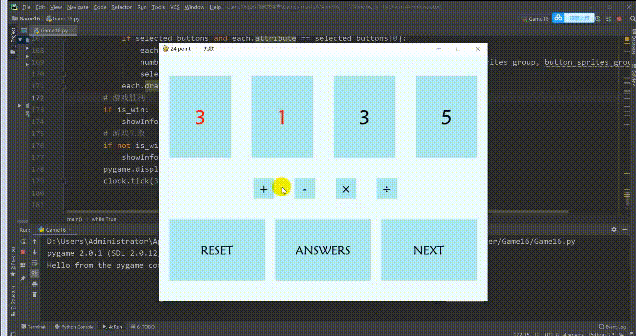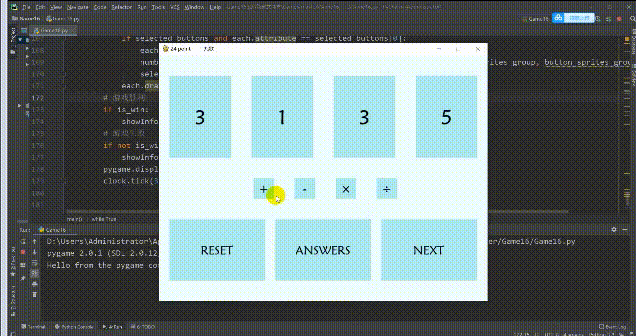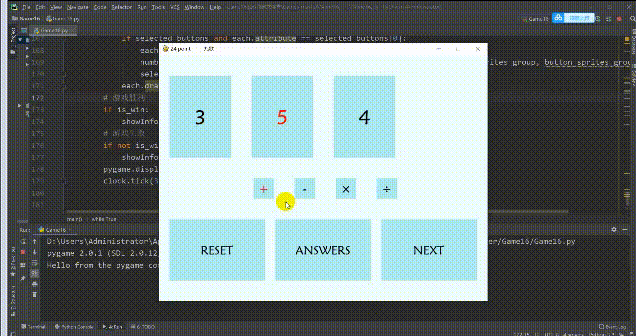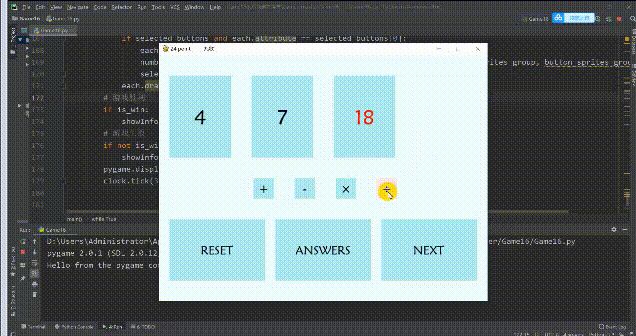
源码分享:
import os
import sys
import pygame
from cfg import *
from modules import *
from fractions import Fraction'''检查控件是否被点击'''
def checkClicked(group, mouse_pos, group_type='NUMBER'):selected = []# 数字卡片/运算符卡片if group_type == GROUPTYPES[0] or group_type == GROUPTYPES[1]:max_selected = 2 if group_type == GROUPTYPES[0] else 1num_selected = 0for each in group:num_selected += int(each.is_selected)for each in group:if each.rect.collidepoint(mouse_pos):if each.is_selected:each.is_selected = not each.is_selectednum_selected -= 1each.select_order = Noneelse:if num_selected < max_selected:each.is_selected = not each.is_selectednum_selected += 1each.select_order = str(num_selected)if each.is_selected:selected.append(each.attribute)# 按钮卡片elif group_type == GROUPTYPES[2]:for each in group:if each.rect.collidepoint(mouse_pos):each.is_selected = Trueselected.append(each.attribute)# 抛出异常else:raise ValueError('checkClicked.group_type unsupport %s, expect %s, %s or %s...' % (group_type, *GROUPTYPES))return selected'''获取数字精灵组'''
def getNumberSpritesGroup(numbers):number_sprites_group = pygame.sprite.Group()for idx, number in enumerate(numbers):args = (*NUMBERCARD_POSITIONS[idx], str(number), NUMBERFONT, NUMBERFONT_COLORS, NUMBERCARD_COLORS, str(number))number_sprites_group.add(Card(*args))return number_sprites_group'''获取运算符精灵组'''
def getOperatorSpritesGroup(operators):operator_sprites_group = pygame.sprite.Group()for idx, operator in enumerate(operators):args = (*OPERATORCARD_POSITIONS[idx], str(operator), OPERATORFONT, OPREATORFONT_COLORS, OPERATORCARD_COLORS, str(operator))operator_sprites_group.add(Card(*args))return operator_sprites_group'''获取按钮精灵组'''
def getButtonSpritesGroup(buttons):button_sprites_group = pygame.sprite.Group()for idx, button in enumerate(buttons):args = (*BUTTONCARD_POSITIONS[idx], str(button), BUTTONFONT, BUTTONFONT_COLORS, BUTTONCARD_COLORS, str(button))button_sprites_group.add(Button(*args))return button_sprites_group'''计算'''
def calculate(number1, number2, operator):operator_map = {'+': '+', '-': '-', '×': '*', '÷': '/'}try:result = str(eval(number1+operator_map[operator]+number2))return result if '.' not in result else str(Fraction(number1+operator_map[operator]+number2))except:return None'''在屏幕上显示信息'''
def showInfo(text, screen):rect = pygame.Rect(200, 180, 400, 200)pygame.draw.rect(screen, PAPAYAWHIP, rect)font = pygame.font.Font(FONTPATH, 40)text_render = font.render(text, True, BLACK)font_size = font.size(text)screen.blit(text_render, (rect.x+(rect.width-font_size[0])/2, rect.y+(rect.height-font_size[1])/2))'''主函数'''
def main():# 初始化, 导入必要的游戏素材pygame.init()pygame.mixer.init()screen = pygame.display.set_mode(SCREENSIZE)pygame.display.set_caption('24 point —— 九歌')win_sound = pygame.mixer.Sound(AUDIOWINPATH)lose_sound = pygame.mixer.Sound(AUDIOLOSEPATH)warn_sound = pygame.mixer.Sound(AUDIOWARNPATH)pygame.mixer.music.load(BGMPATH)pygame.mixer.music.play(-1, 0.0)# 24点游戏生成器game24_gen = game24Generator()game24_gen.generate()# 精灵组# --数字number_sprites_group = getNumberSpritesGroup(game24_gen.numbers_now)# --运算符operator_sprites_group = getOperatorSpritesGroup(OPREATORS)# --按钮button_sprites_group = getButtonSpritesGroup(BUTTONS)# 游戏主循环clock = pygame.time.Clock()selected_numbers = []selected_operators = []selected_buttons = []is_win = Falsewhile True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit(-1)elif event.type == pygame.MOUSEBUTTONUP:mouse_pos = pygame.mouse.get_pos()selected_numbers = checkClicked(number_sprites_group, mouse_pos, 'NUMBER')selected_operators = checkClicked(operator_sprites_group, mouse_pos, 'OPREATOR')selected_buttons = checkClicked(button_sprites_group, mouse_pos, 'BUTTON')screen.fill(AZURE)# 更新数字if len(selected_numbers) == 2 and len(selected_operators) == 1:noselected_numbers = []for each in number_sprites_group:if each.is_selected:if each.select_order == '1':selected_number1 = each.attributeelif each.select_order == '2':selected_number2 = each.attributeelse:raise ValueError('Unknow select_order %s, expect 1 or 2...' % each.select_order)else:noselected_numbers.append(each.attribute)each.is_selected = Falsefor each in operator_sprites_group:each.is_selected = Falseresult = calculate(selected_number1, selected_number2, *selected_operators)if result is not None:game24_gen.numbers_now = noselected_numbers + [result]is_win = game24_gen.check()if is_win:win_sound.play()if not is_win and len(game24_gen.numbers_now) == 1:lose_sound.play()else:warn_sound.play()selected_numbers = []selected_operators = []number_sprites_group = getNumberSpritesGroup(game24_gen.numbers_now)# 精灵都画到screen上for each in number_sprites_group:each.draw(screen, pygame.mouse.get_pos())for each in operator_sprites_group:each.draw(screen, pygame.mouse.get_pos())for each in button_sprites_group:if selected_buttons and selected_buttons[0] in ['RESET', 'NEXT']:is_win = Falseif selected_buttons and each.attribute == selected_buttons[0]:each.is_selected = Falsenumber_sprites_group = each.do(game24_gen, getNumberSpritesGroup, number_sprites_group, button_sprites_group)selected_buttons = []each.draw(screen, pygame.mouse.get_pos())# 游戏胜利if is_win:showInfo('Congratulations', screen)# 游戏失败if not is_win and len(game24_gen.numbers_now) == 1:showInfo('Game Over', screen)pygame.display.flip()clock.tick(30)'''run'''
if __name__ == '__main__':main()11、平衡木
玩法:也是小时候的经典游戏,控制左右就行,到后面才有一点点难度。
源码分享:
import cfg
from modules import breakoutClone'''主函数'''
def main():game = breakoutClone(cfg)game.run()'''run'''
if __name__ == '__main__':main()
12、外星人入侵
玩法:这让我想起了魂斗罗那第几关的boss,有点类似,不过魂斗罗那个难度肯定高点。

源码分享:
import os
import sys
import cfg
import random
import pygame
from modules import *'''开始游戏'''
def startGame(screen):clock = pygame.time.Clock()# 加载字体font = pygame.font.SysFont('arial', 18)if not os.path.isfile('score'):f = open('score', 'w')f.write('0')f.close()with open('score', 'r') as f:highest_score = int(f.read().strip())# 敌方enemies_group = pygame.sprite.Group()for i in range(55):if i < 11:enemy = enemySprite('small', i, cfg.WHITE, cfg.WHITE)elif i < 33:enemy = enemySprite('medium', i, cfg.WHITE, cfg.WHITE)else:enemy = enemySprite('large', i, cfg.WHITE, cfg.WHITE)enemy.rect.x = 85 + (i % 11) * 50enemy.rect.y = 120 + (i // 11) * 45enemies_group.add(enemy)boomed_enemies_group = pygame.sprite.Group()en_bullets_group = pygame.sprite.Group()ufo = ufoSprite(color=cfg.RED)# 我方myaircraft = aircraftSprite(color=cfg.GREEN, bullet_color=cfg.WHITE)my_bullets_group = pygame.sprite.Group()# 用于控制敌方位置更新# --移动一行enemy_move_count = 24enemy_move_interval = 24enemy_move_flag = False# --改变移动方向(改变方向的同时集体下降一次)enemy_change_direction_count = 0enemy_change_direction_interval = 60enemy_need_down = Falseenemy_move_right = Trueenemy_need_move_row = 6enemy_max_row = 5# 用于控制敌方发射子弹enemy_shot_interval = 100enemy_shot_count = 0enemy_shot_flag = False# 游戏进行中running = Trueis_win = False# 主循环while running:screen.fill(cfg.BLACK)for event in pygame.event.get():# --点右上角的X或者按Esc键退出游戏if event.type == pygame.QUIT:pygame.quit()sys.exit()if event.type == pygame.KEYDOWN:if event.key == pygame.K_ESCAPE:pygame.quit()sys.exit()# --射击if event.type == pygame.MOUSEBUTTONDOWN:my_bullet = myaircraft.shot()if my_bullet:my_bullets_group.add(my_bullet)# --我方子弹与敌方/UFO碰撞检测for enemy in enemies_group:if pygame.sprite.spritecollide(enemy, my_bullets_group, True, None):boomed_enemies_group.add(enemy)enemies_group.remove(enemy)myaircraft.score += enemy.rewardif pygame.sprite.spritecollide(ufo, my_bullets_group, True, None):ufo.is_dead = Truemyaircraft.score += ufo.reward# --更新并画敌方# ----敌方子弹enemy_shot_count += 1if enemy_shot_count > enemy_shot_interval:enemy_shot_flag = Trueenemies_survive_list = [enemy.number for enemy in enemies_group]shot_number = random.choice(enemies_survive_list)enemy_shot_count = 0# ----敌方移动enemy_move_count += 1if enemy_move_count > enemy_move_interval:enemy_move_count = 0enemy_move_flag = Trueenemy_need_move_row -= 1if enemy_need_move_row == 0:enemy_need_move_row = enemy_max_rowenemy_change_direction_count += 1if enemy_change_direction_count > enemy_change_direction_interval:enemy_change_direction_count = 1enemy_move_right = not enemy_move_rightenemy_need_down = True# ----每次下降提高移动和射击速度enemy_move_interval = max(15, enemy_move_interval-3)enemy_shot_interval = max(50, enemy_move_interval-10)# ----遍历更新for enemy in enemies_group:if enemy_shot_flag:if enemy.number == shot_number:en_bullet = enemy.shot()en_bullets_group.add(en_bullet)if enemy_move_flag:if enemy.number in range((enemy_need_move_row-1)*11, enemy_need_move_row*11):if enemy_move_right:enemy.update('right', cfg.SCREENSIZE[1])else:enemy.update('left', cfg.SCREENSIZE[1])else:enemy.update(None, cfg.SCREENSIZE[1])if enemy_need_down:if enemy.update('down', cfg.SCREENSIZE[1]):running = Falseis_win = Falseenemy.change_count -= 1enemy.draw(screen)enemy_move_flag = Falseenemy_need_down = Falseenemy_shot_flag = False# ----敌方爆炸特效for boomed_enemy in boomed_enemies_group:if boomed_enemy.boom(screen):boomed_enemies_group.remove(boomed_enemy)del boomed_enemy# --敌方子弹与我方飞船碰撞检测if not myaircraft.one_dead:if pygame.sprite.spritecollide(myaircraft, en_bullets_group, True, None):myaircraft.one_dead = Trueif myaircraft.one_dead:if myaircraft.boom(screen):myaircraft.resetBoom()myaircraft.num_life -= 1if myaircraft.num_life < 1:running = Falseis_win = Falseelse:# ----更新飞船myaircraft.update(cfg.SCREENSIZE[0])# ----画飞船myaircraft.draw(screen)if (not ufo.has_boomed) and (ufo.is_dead):if ufo.boom(screen):ufo.has_boomed = Trueelse:# ----更新UFOufo.update(cfg.SCREENSIZE[0])# ----画UFOufo.draw(screen)# --画我方飞船子弹for bullet in my_bullets_group:if bullet.update():my_bullets_group.remove(bullet)del bulletelse:bullet.draw(screen)# --画敌方子弹for bullet in en_bullets_group:if bullet.update(cfg.SCREENSIZE[1]):en_bullets_group.remove(bullet)del bulletelse:bullet.draw(screen)if myaircraft.score > highest_score:highest_score = myaircraft.score# --得分每增加2000我方飞船增加一条生命if (myaircraft.score % 2000 == 0) and (myaircraft.score > 0) and (myaircraft.score != myaircraft.old_score):myaircraft.old_score = myaircraft.scoremyaircraft.num_life = min(myaircraft.num_life + 1, myaircraft.max_num_life)# --敌人都死光了的话就胜利了if len(enemies_group) < 1:is_win = Truerunning = False# --显示文字# ----当前得分showText(screen, 'SCORE: ', cfg.WHITE, font, 200, 8)showText(screen, str(myaircraft.score), cfg.WHITE, font, 200, 24)# ----敌人数量showText(screen, 'ENEMY: ', cfg.WHITE, font, 370, 8)showText(screen, str(len(enemies_group)), cfg.WHITE, font, 370, 24)# ----历史最高分showText(screen, 'HIGHEST: ', cfg.WHITE, font, 540, 8)showText(screen, str(highest_score), cfg.WHITE, font, 540, 24)# ----FPSshowText(screen, 'FPS: ' + str(int(clock.get_fps())), cfg.RED, font, 8, 8)# --显示剩余生命值showLife(screen, myaircraft.num_life, cfg.GREEN)pygame.display.update()clock.tick(cfg.FPS)with open('score', 'w') as f:f.write(str(highest_score))return is_win'''主函数'''
def main():# 初始化pygame.init()pygame.display.set_caption('外星人入侵 —— 九歌')screen = pygame.display.set_mode(cfg.SCREENSIZE)pygame.mixer.init()pygame.mixer.music.load(cfg.BGMPATH)pygame.mixer.music.set_volume(0.4)pygame.mixer.music.play(-1)while True:is_win = startGame(screen)endInterface(screen, cfg.BLACK, is_win)'''run'''
if __name__ == '__main__':main()
13、井字棋888
玩法:我打赌大家在课堂上肯定玩过这个,想想当年和同桌玩这个废了好几本本子。
源码分享
from tkinter import *
import tkinter.messagebox as msgroot = Tk()
root.title('TIC-TAC-TOE---Project Gurukul')
# labels
Label(root, text="player1 : X", font="times 15").grid(row=0, column=1)
Label(root, text="player2 : O", font="times 15").grid(row=0, column=2)digits = [1, 2, 3, 4, 5, 6, 7, 8, 9]# for player1 sign = X and for player2 sign= Y
mark = ''# counting the no. of click
count = 0panels = ["panel"] * 10def win(panels, sign):return ((panels[1] == panels[2] == panels[3] == sign)or (panels[1] == panels[4] == panels[7] == sign)or (panels[1] == panels[5] == panels[9] == sign)or (panels[2] == panels[5] == panels[8] == sign)or (panels[3] == panels[6] == panels[9] == sign)or (panels[3] == panels[5] == panels[7] == sign)or (panels[4] == panels[5] == panels[6] == sign)or (panels[7] == panels[8] == panels[9] == sign))def checker(digit):global count, mark, digits# Check which button clickedif digit == 1 and digit in digits:digits.remove(digit)##player1 will play if the value of count is even and for odd player2 will playif count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton1.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 2 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton2.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 3 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton3.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 4 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton4.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 5 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton5.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 6 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton6.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 7 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton7.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 8 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton8.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()if digit == 9 and digit in digits:digits.remove(digit)if count % 2 == 0:mark = 'X'panels[digit] = markelif count % 2 != 0:mark = 'O'panels[digit] = markbutton9.config(text=mark)count = count + 1sign = markif (win(panels, sign) and sign == 'X'):msg.showinfo("Result", "Player1 wins")root.destroy()elif (win(panels, sign) and sign == 'O'):msg.showinfo("Result", "Player2 wins")root.destroy()###if count is greater then 8 then the match has been tiedif (count > 8 and win(panels, 'X') == False and win(panels, 'O') == False):msg.showinfo("Result", "Match Tied")root.destroy()####define buttons
button1 = Button(root, width=15, font=('Times 16 bold'), height=7, command=lambda: checker(1))
button1.grid(row=1, column=1)
button2 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(2))
button2.grid(row=1, column=2)
button3 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(3))
button3.grid(row=1, column=3)
button4 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(4))
button4.grid(row=2, column=1)
button5 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(5))
button5.grid(row=2, column=2)
button6 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(6))
button6.grid(row=2, column=3)
button7 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(7))
button7.grid(row=3, column=1)
button8 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(8))
button8.grid(row=3, column=2)
button9 = Button(root, width=15, height=7, font=('Times 16 bold'), command=lambda: checker(9))
button9.grid(row=3, column=3)root.mainloop()
