php企业网站开发源码网站关键字布局
文章目录
- 前言
- 一、红黑树的插入操作
- 1.红黑树结点的定义
- 2.红黑树的插入
- 1.uncle存在且为红
- 2.uncle不存在
- 3.uncle存在且为黑
- 3.完整代码
- 二、是否为红黑树的验证
- 1.IsBlance函数
- 2.CheckColor函数
- 三、红黑树与AVL树的比较
前言
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的
红黑树的性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点 (每条路径上的黑色结点数量相同)
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
最短路径:全部都是黑节点的路径。
最长路径:一黑一红相间的路径
一、红黑树的插入操作
1.红黑树结点的定义
enum Color {RED,BLACK
};
template<class K,class V>
struct RBTreeNode {RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;pair<K, V>_kv;Color _col;//颜色RBTreeNode(const pair<K,V>&kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//结点默认给成红色是为了方便后续的插入//因为默认为黑色的话还需要考虑所有路径上黑色结点数量是否相同//太麻烦了{}
};
2.红黑树的插入
插入分为一下三种情况,因为我们插入的结点默认为红色,而红黑树定义中指出不能出现连续的两个红色结点,为了维持红黑树,我们需要对一些结点的颜色进行改变有时还需要旋转改变树的形状,至于有关旋转的函数Rotate,我已经在之前AVL树的模拟实现中详细说明了,这里就不多在赘述了【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子),有需要的可以去看一下。
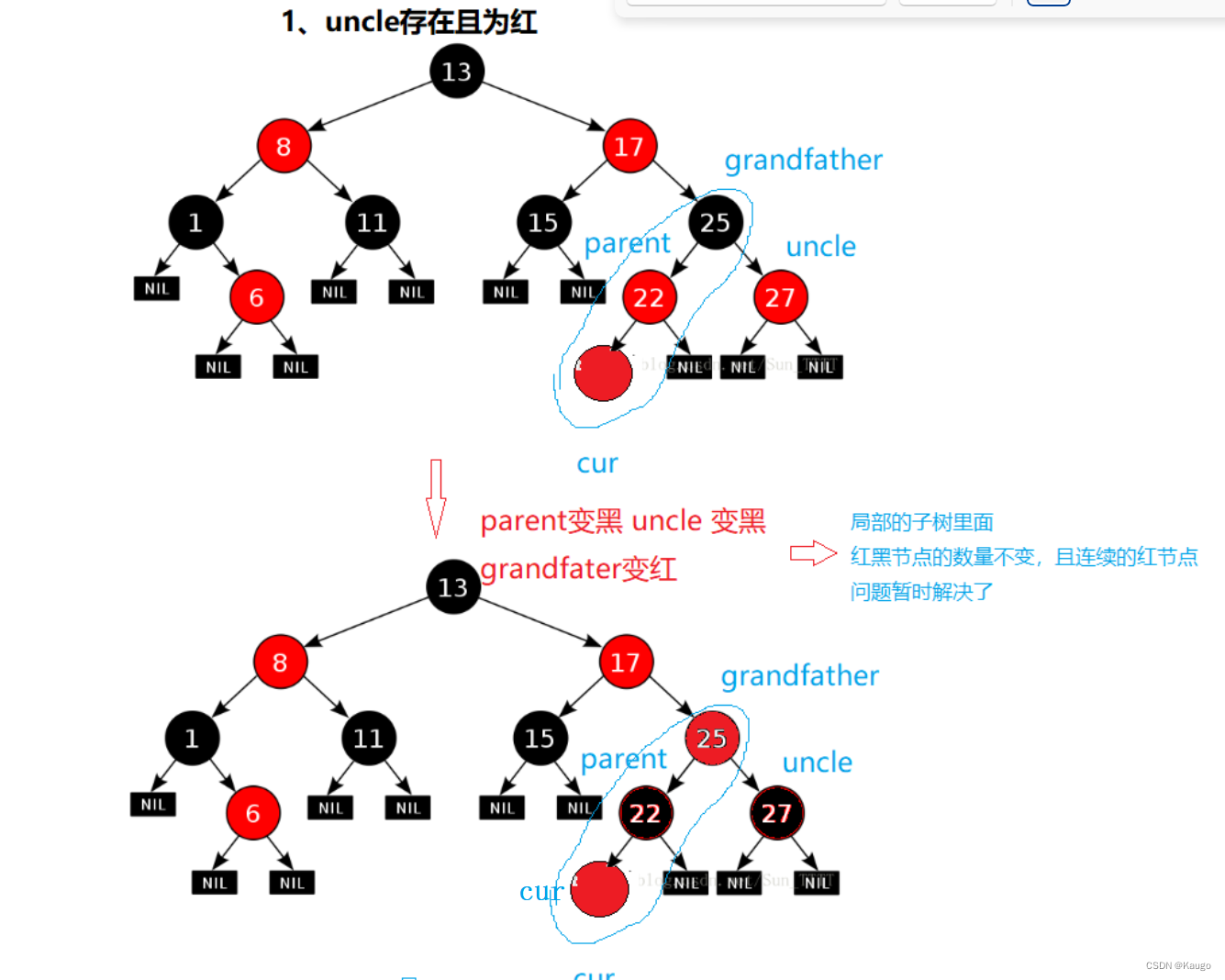
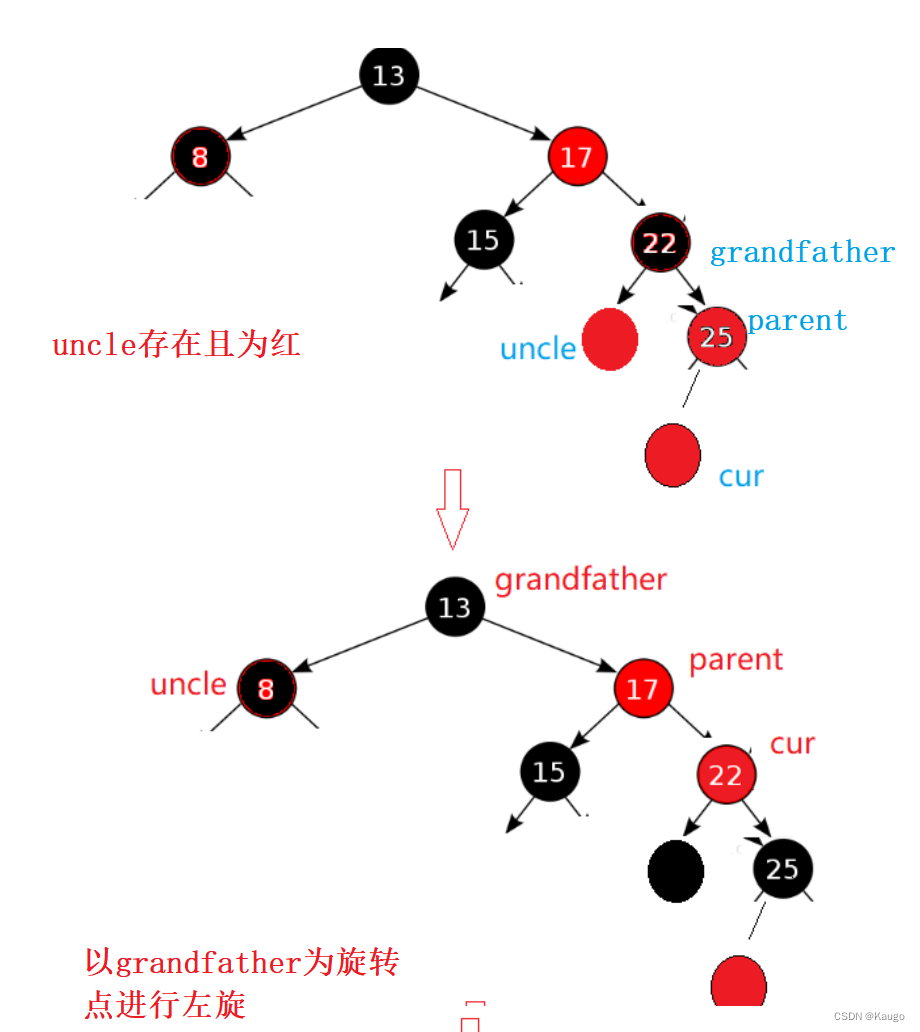
1.uncle存在且为红
这种情况就不需要考虑旋转了
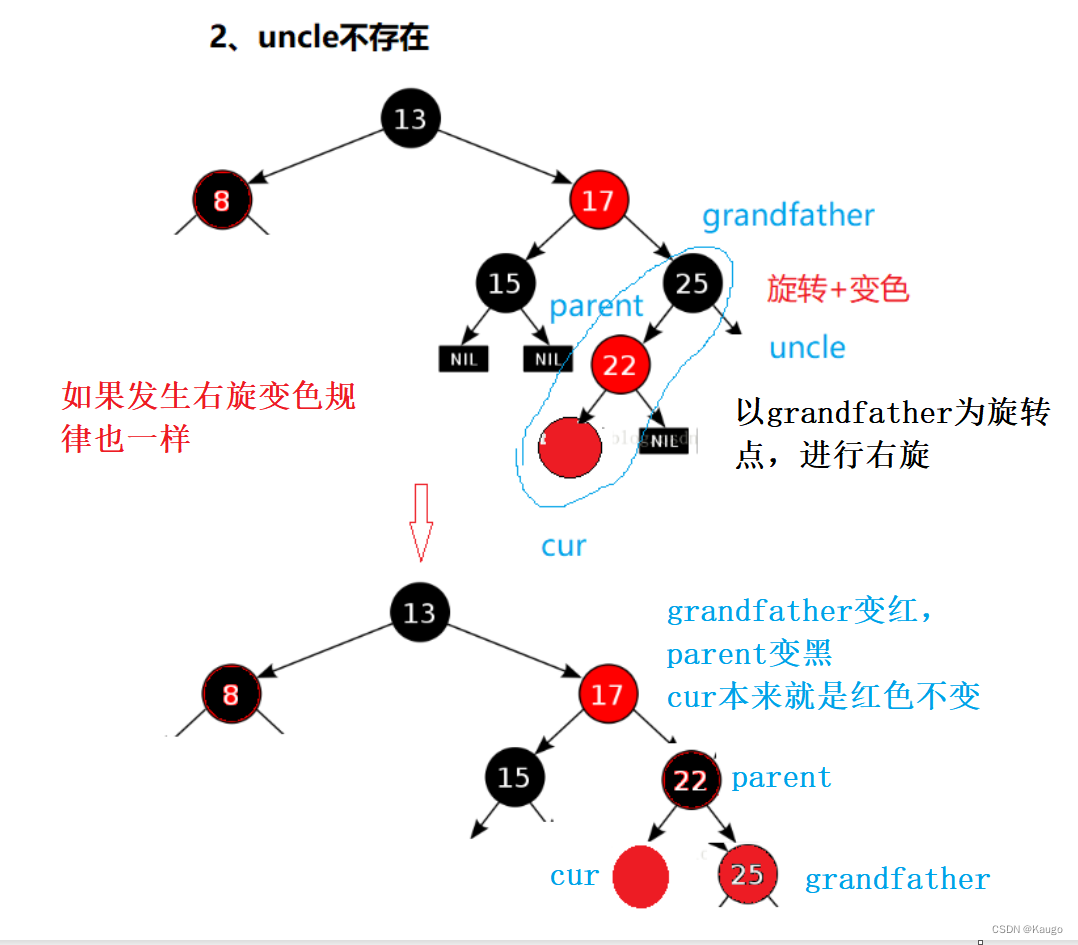
2.uncle不存在
3.uncle存在且为黑

总结:
红黑树插入关键看uncle
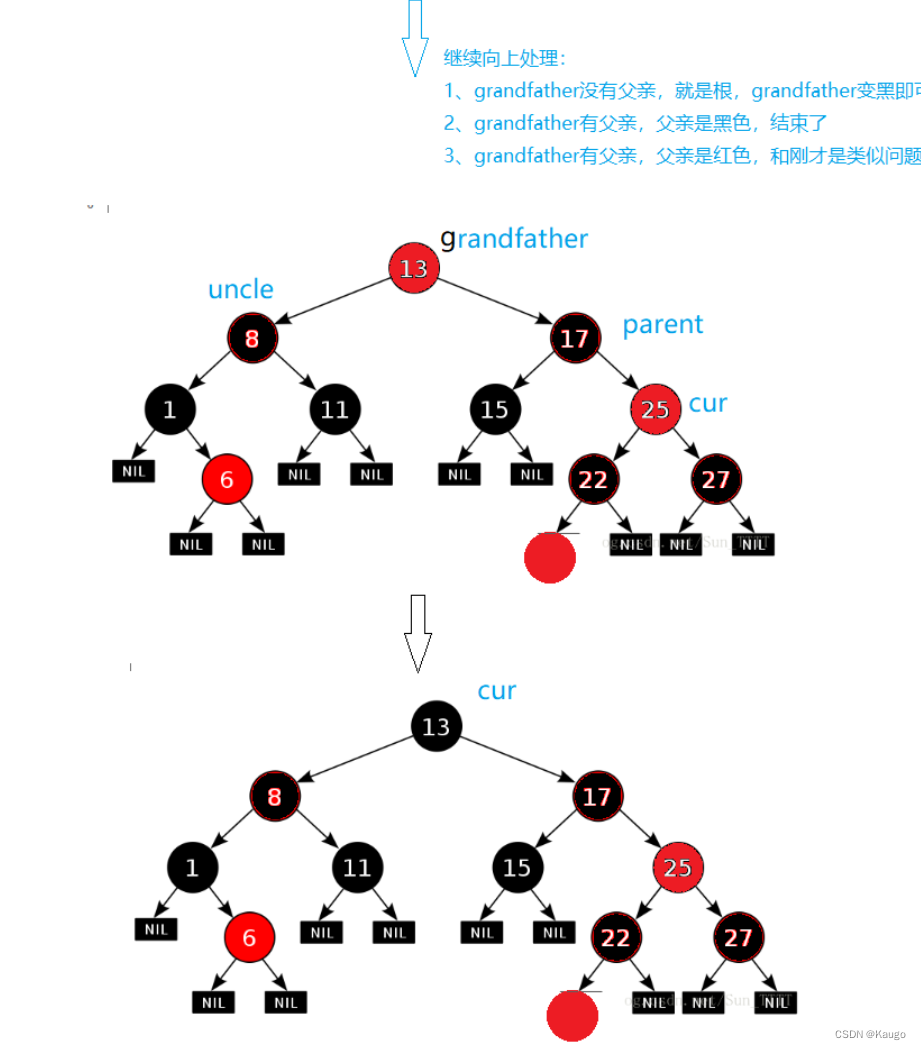
1.uncle存在且为红,变色(uncle与parent变黑色,grandfather变红色),之后继续向上处理
2.uncle不存在或者uncle存在且为黑,旋转加变色,之后break
3.小规律:grandfather在这个过程中要不本来就为红色,要不就变成红色
3.完整代码
template<class K,class V>
class RBTree {typedef RBTreeNode<K,V> Node;
public:bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {//根节点必须为黑色_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {//寻找插入位置if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(kv);cur->_col = RED;//插入对应位置,默认为红色if (parent->_kv.first < kv.first) {parent->_right = cur;}else {parent->_left = cur;}cur->_parent = parent;//让新插入结点指向父亲while (parent && parent->_col == RED) {Node* grandfather = parent->_parent;if (parent = grandfather->_left) {Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED) {//uncle存在且为红parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}else {//uncle不存在或者uncle为黑if (cur == parent->_left) {// g// p// cRotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else {// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else {// parent == grandfather->_rightNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED) {//uncle存在且为红parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}else {//uncle不存在或者uncle为黑if (cur == parent->_right) {// g// p// cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else {// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;//根节点必须为黑色return true;}void RotateL(Node* parent) {//左旋Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft) {curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;if (ppnode == nullptr) {_root = cur;cur->_parent = nullptr;}else {if (ppnode->_left = parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent) {//右旋Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright) {curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr) {_root = cur;cur->_parent = nullptr;}else {if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}}
};
二、是否为红黑树的验证
1.IsBlance函数
bool IsBalance() {return IsBalance(_root);}bool IsBalance(Node* root) {if (root == nullptr) {return true;}if (root->_col != BLACK) {return false;}//根节点一定为黑色int benchmark = 0;Node* cur = _root;while (cur) {//算出最左边黑色结点的数目,为了与//其他路径黑色结点的数目作比较if (cur->_col == BLACK) {benchmark++;}cur = cur->_left;}return CheckColor(root, 0, benchmark);}
2.CheckColor函数
bool CheckColor(Node* root, int blacknum, int benchmark) {if (root == nullptr) {//root为空说明已经数完了一条路径的黑色结点//与原先数的最左的黑色节点数进行比较if (blacknum != benchmark) {return false;}return true;}if (root->_col == BLACK) {blacknum++;//当前路径黑色结点树++}if (root->_col == RED && root->_parent && root->_parent->_col == RED) {cout << root->_kv.first << "出现连续红色节点" << endl;//判断是否出现连续的红色结点return false;}//递归式对左右子树分别检验return CheckColor(root->_left, blacknum, benchmark) && CheckColor(root->_right, blacknum, benchmark);}
三、红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追
求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,
所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红
黑树更多。