网站忘记后台地址设计说明翻译
1 接口
ether3 出接口
ether4 内网接口
2 出接口
出接口采用PPPoE拨号SLAAC获取前缀,手动配置后缀
2.1 选择出接口interface,配置PPPoE client模式

2.2 配置PPPoE client用户名和密码
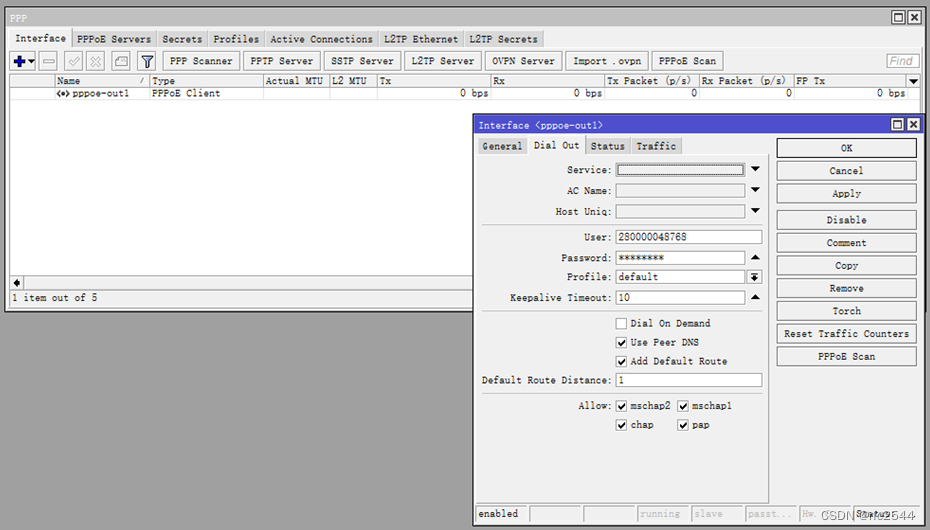
2.3 从PPPoE client获取前缀地址池

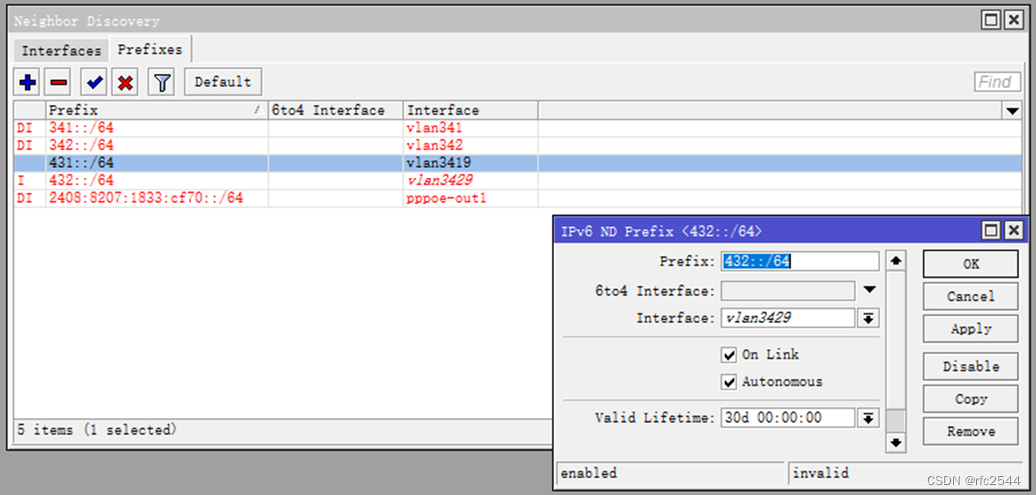
2.4 给出接口选择前缀并配置后缀

3 NAT
3.1 IPv4 NAT
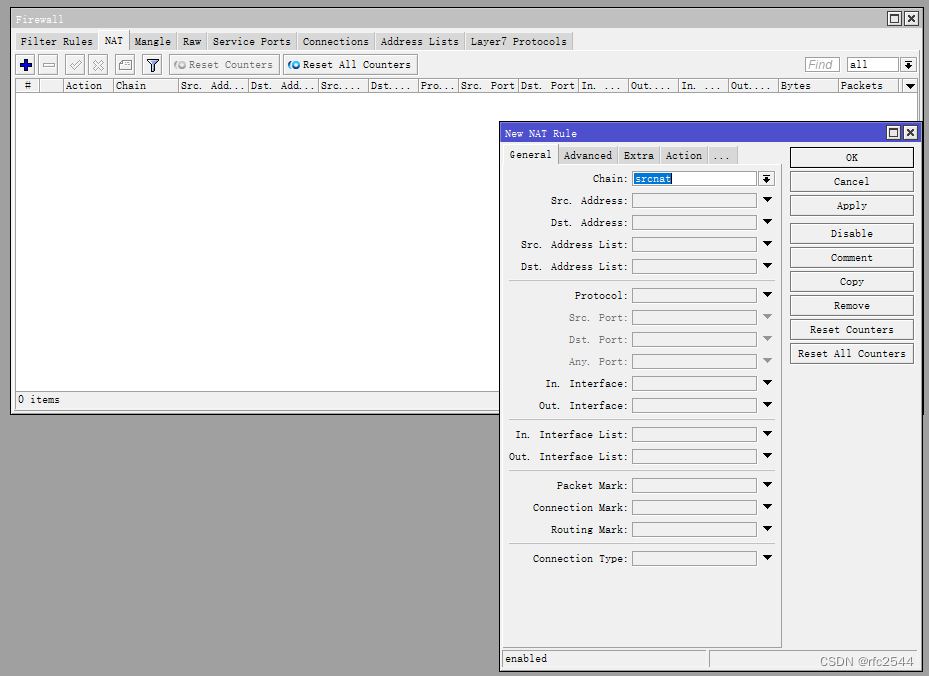

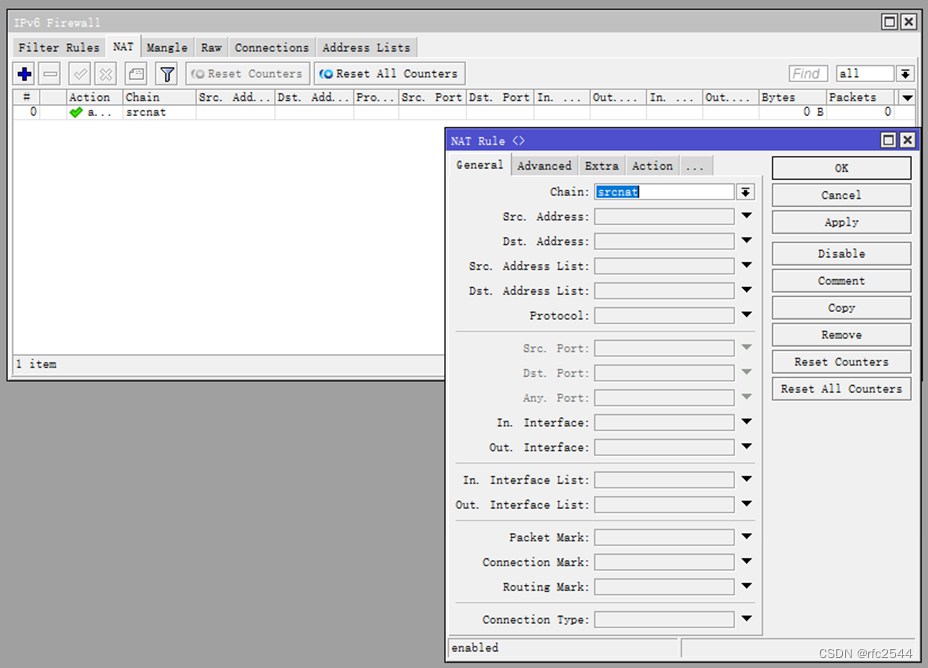
3.2 IPv6 NAT

4 DNS Proxy

5 内网
起两套环境,一个vlan341,一个vlan342
5.1 interface

5.2 vlan


5.3 IPv4 pool
IPv4 DHCPv4地址池
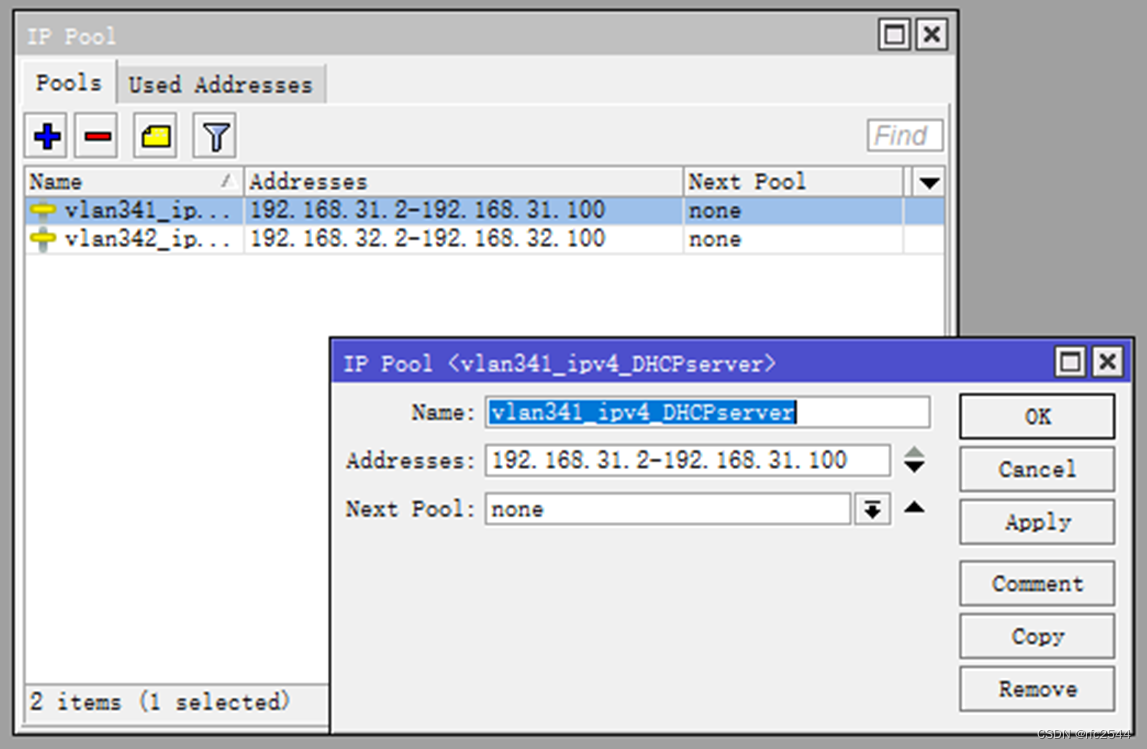

IPv4 PPPoE地址池

5.4 vlan接口 IPoE IPv4 address
这是给IPv4 IPoE用的,IPv4 PPPoE因为是p2p的在起PPPoEv4server的时候会自动起虚拟接口IP


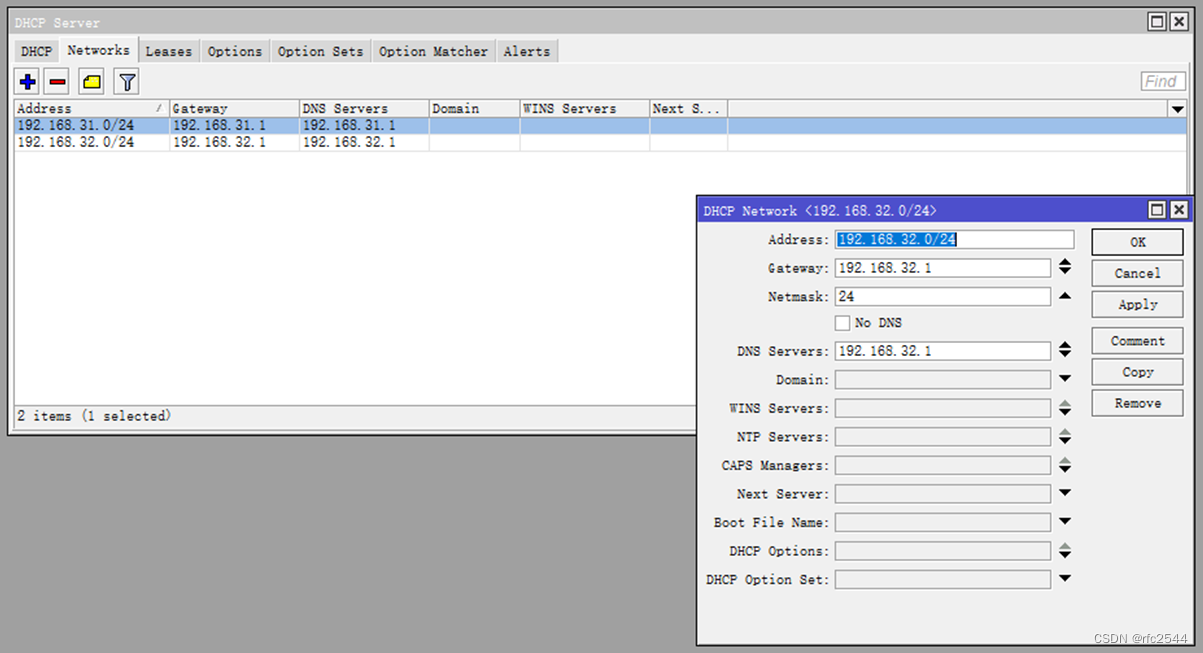
5.5 IPv4 DHCPserver

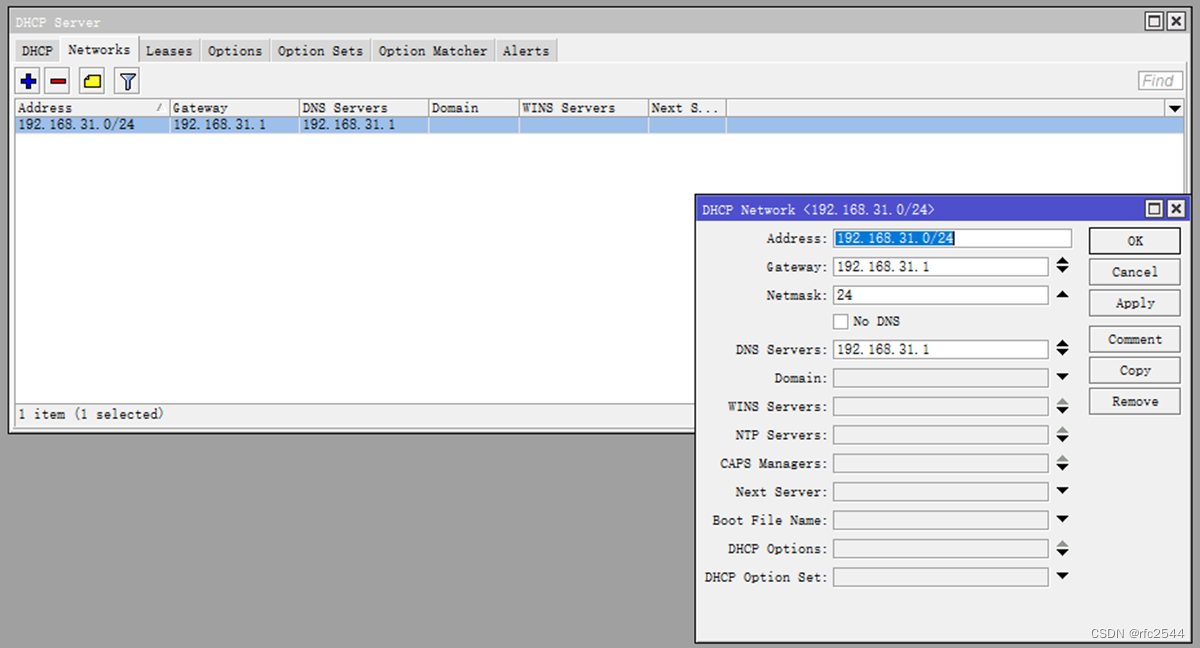
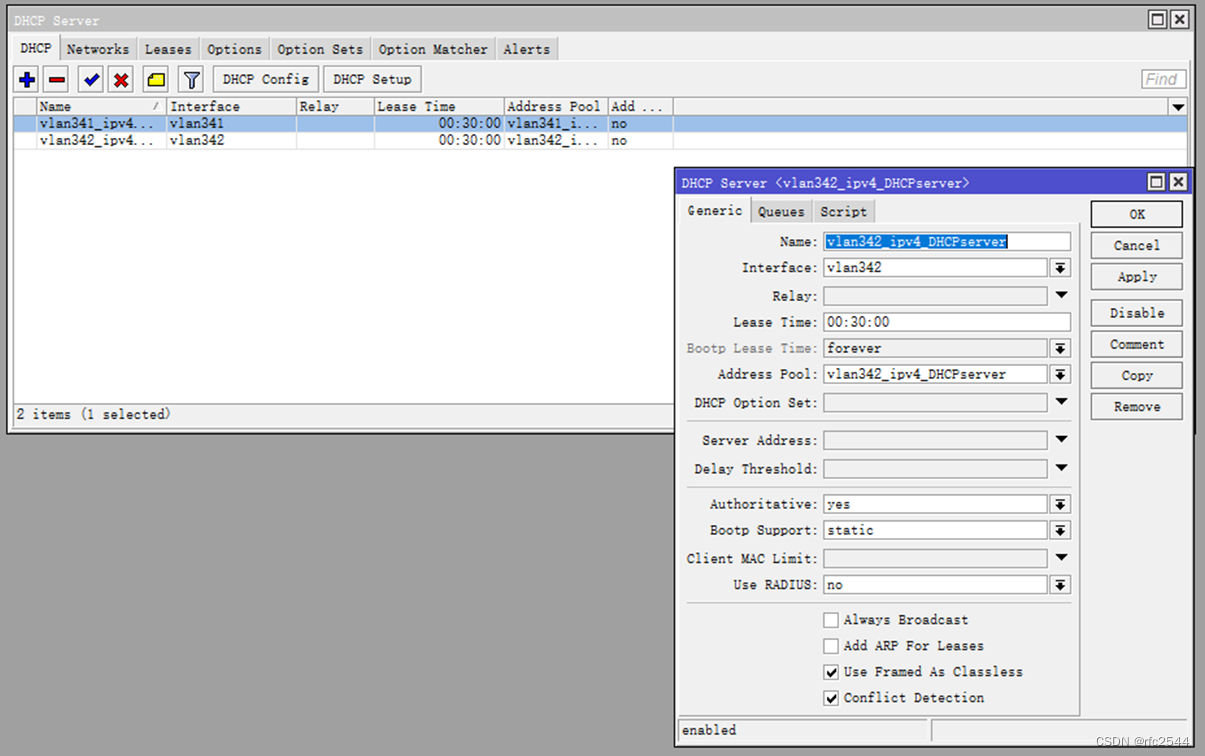
5.6 IPv4 PPPoEserver
5.6.1 profile
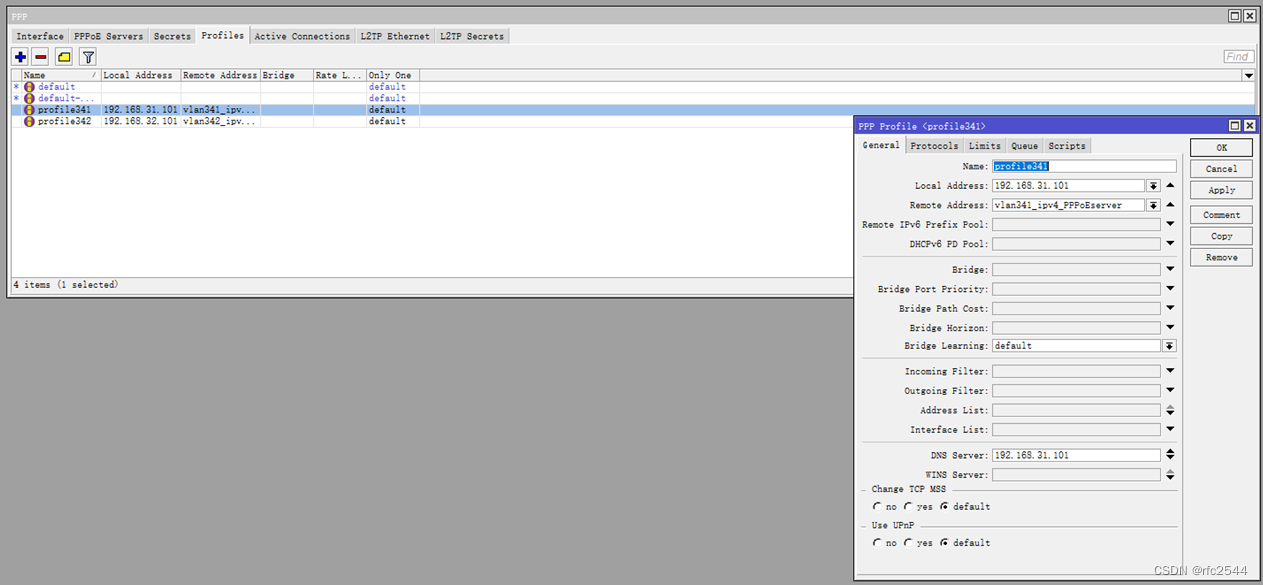
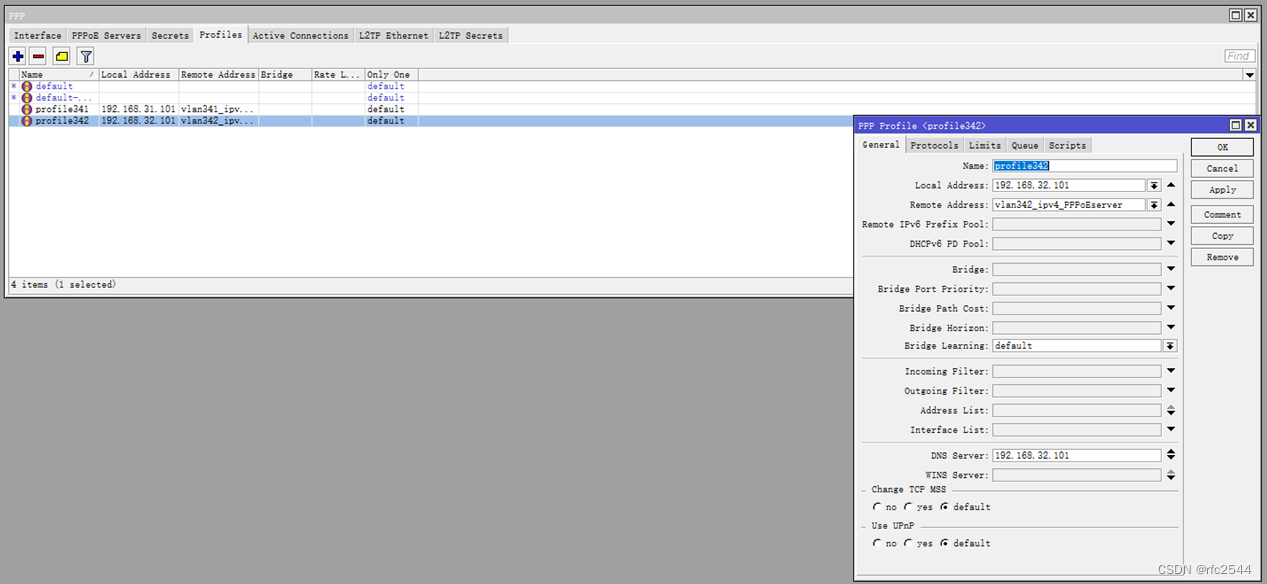
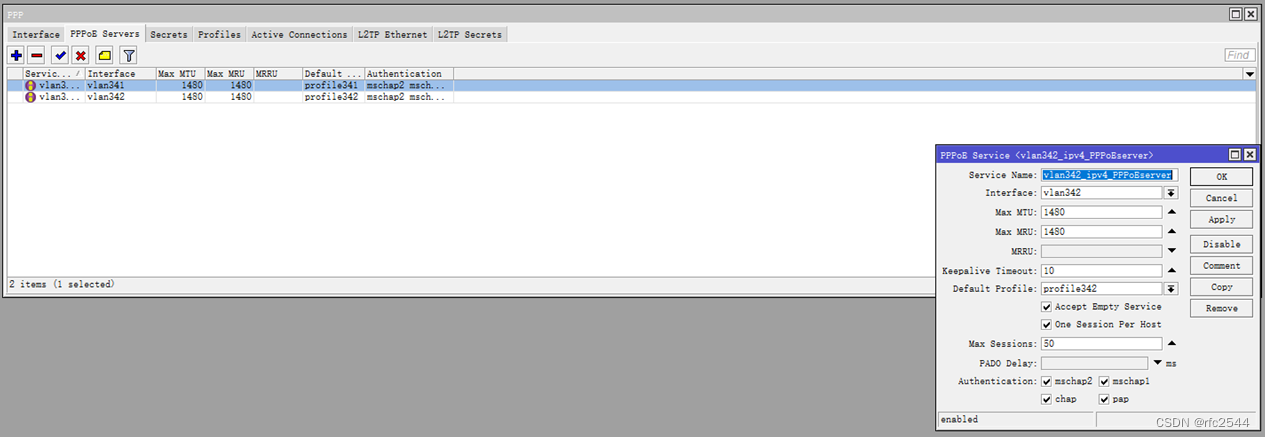
5.6.2 IPv4 PPPoEserver

5.6.3 secrets
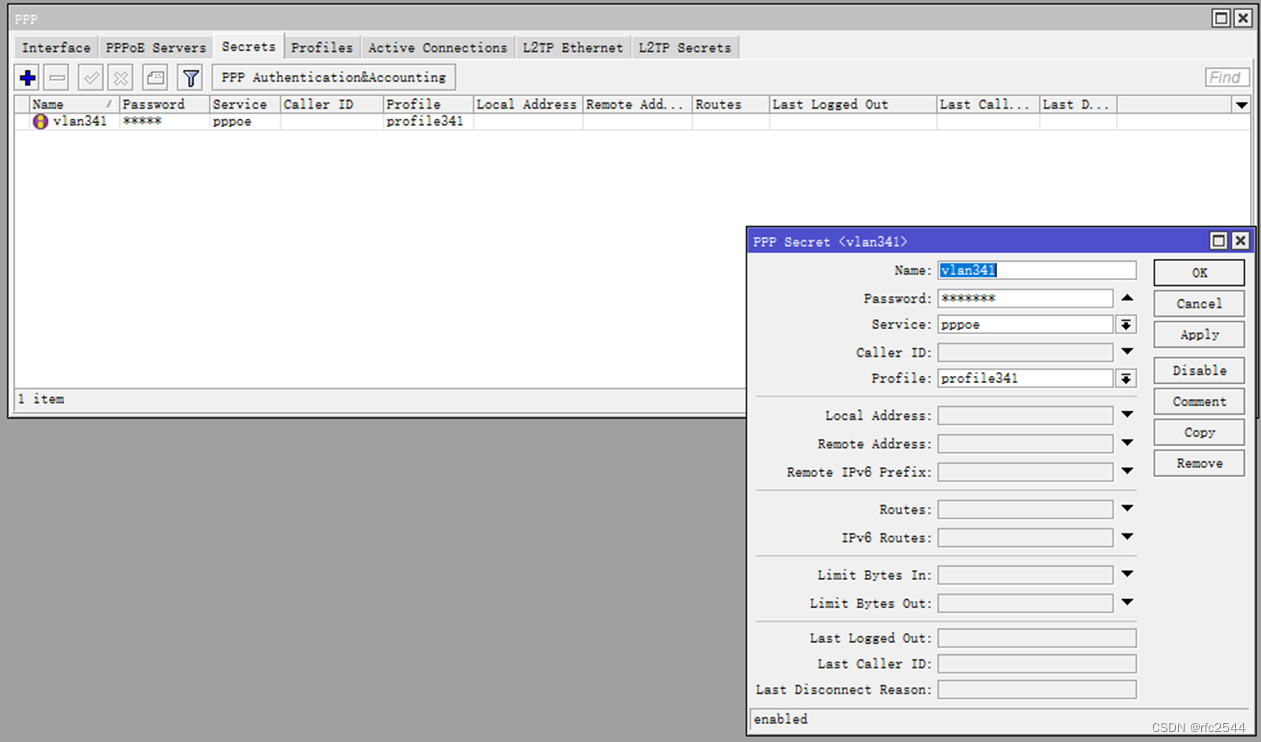
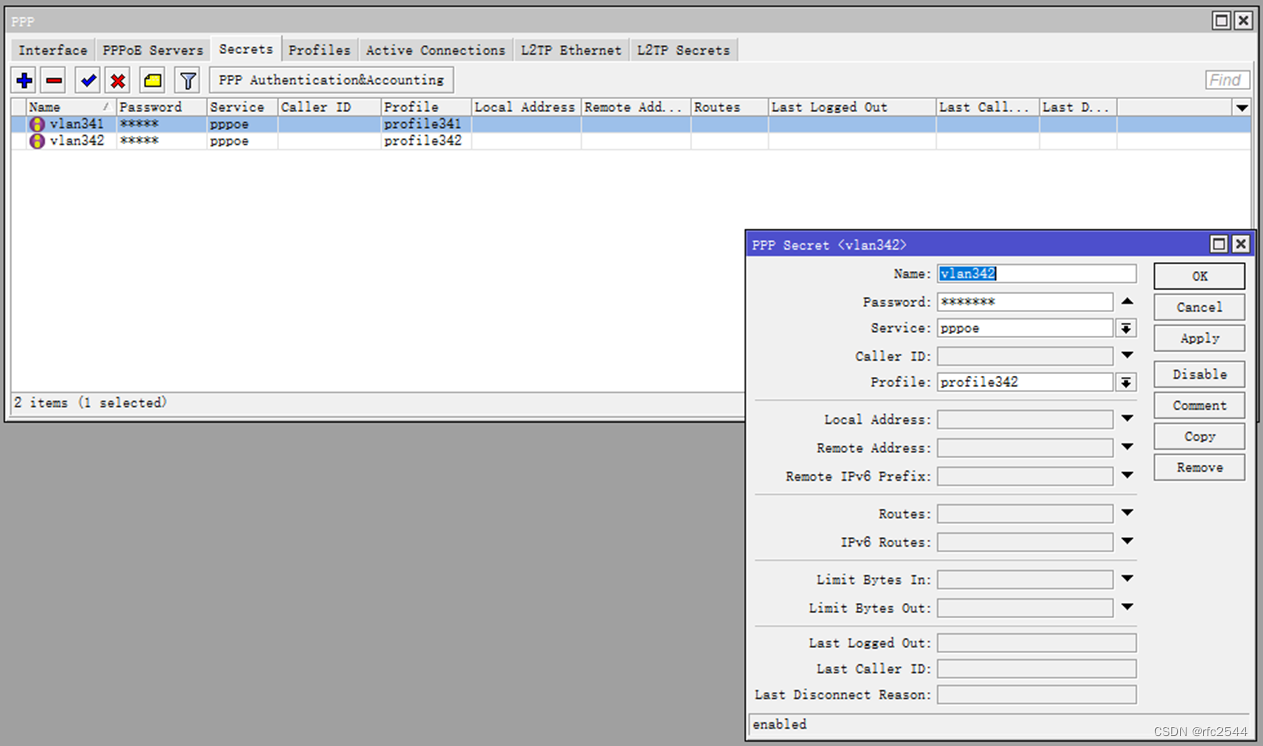
5.7 IPv6 Static address

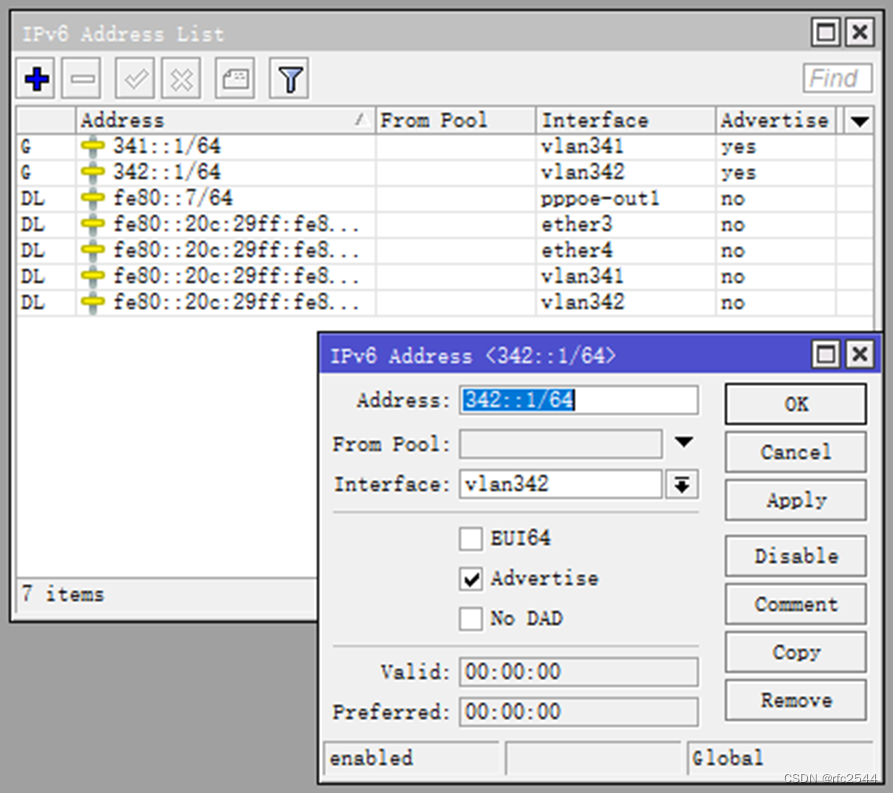
5.7.1 IPv6 static组网指向二级路由器内网的静态路由
二级路由器wan:341::100/64 二级路由器lan:3411::/64
二级路由器wan:342::100/64 二级路由器lan:3422::/64

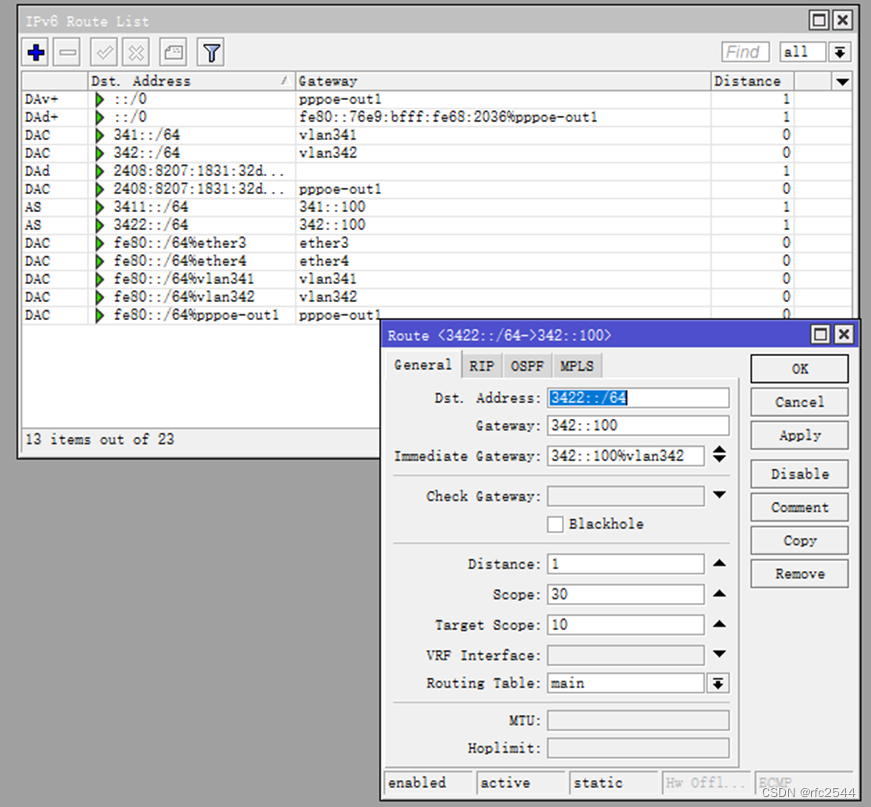
5.8 IPv6 PPPoEserver
5.8.1 PPPoE server binding
User是secret name(步骤5.6.3)
Service是PPPoEv4 Server name(步骤5.6.2)
如果不配置这个,每次二级路由器向其PPPoE拨号,在ROS的PPP的interface会自动生成一个ppp虚接口,这个对v4没啥影响,但是会导致v6的nd失效,即每次二级路由器拨号,都需要在ROS重新配置nd,比较麻烦。


5.8.2 ND RA

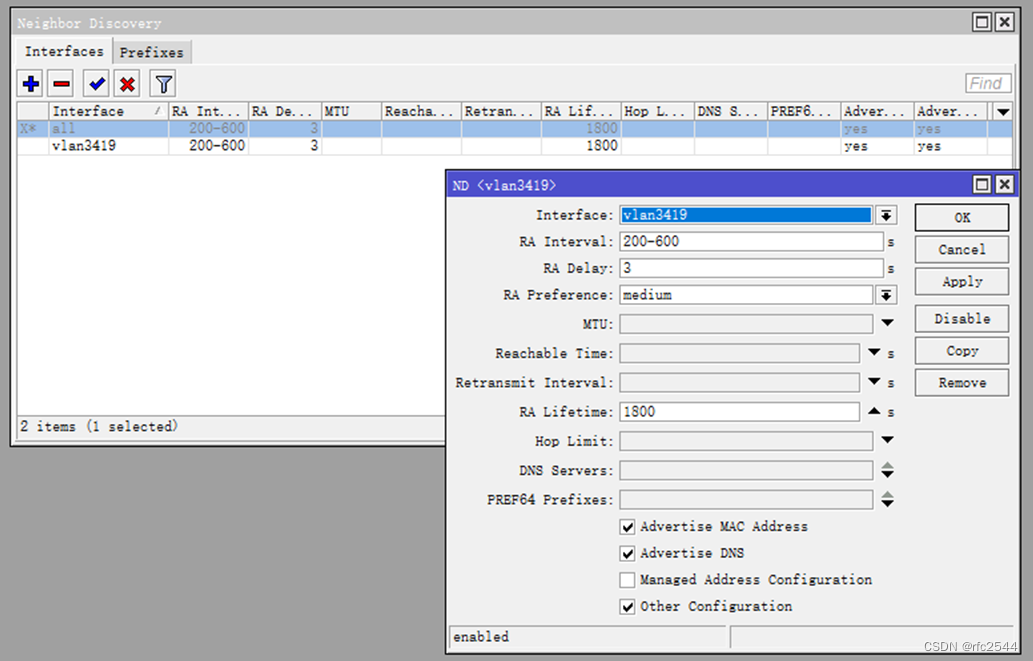
RA携带的给二级路由器wan分配的前缀
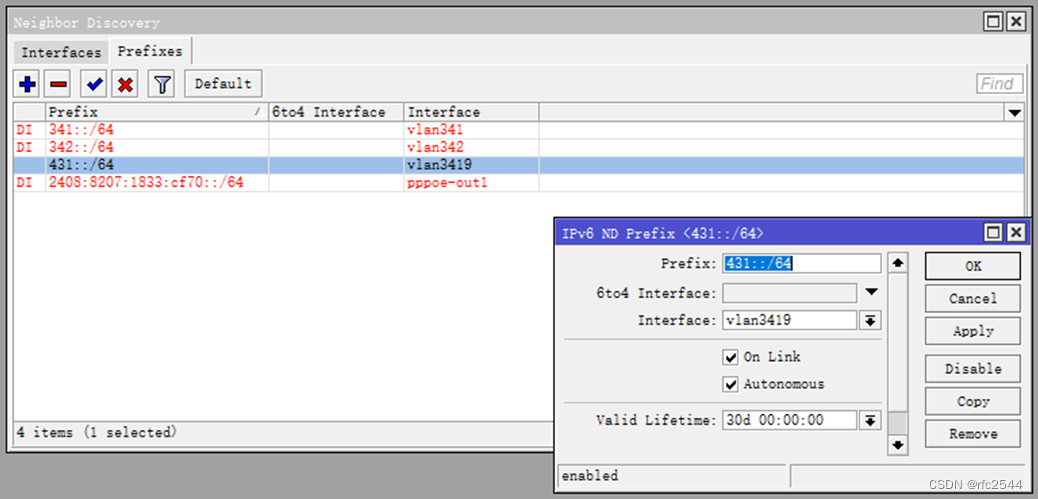
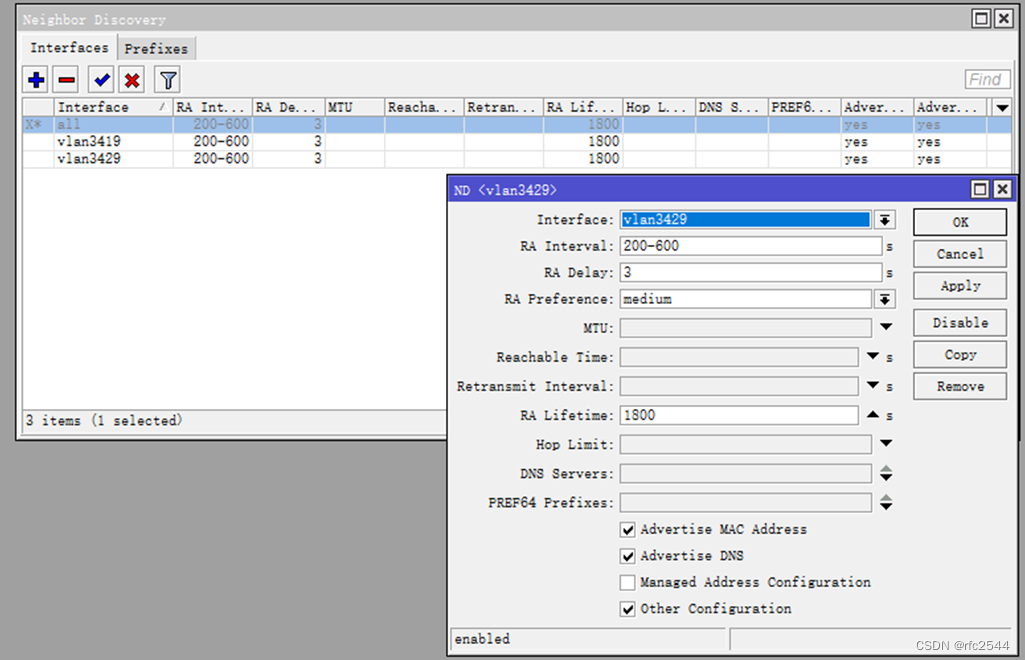
RA携带的给二级路由器wan分配的前缀
5.8.3 IPv6 基于PPPoE之上的IPv6接口address
IPv6比IPv4较特殊,基于PPPoE之上,IPv4是p2p的,而IPv6是在ppp之上封装IPv6

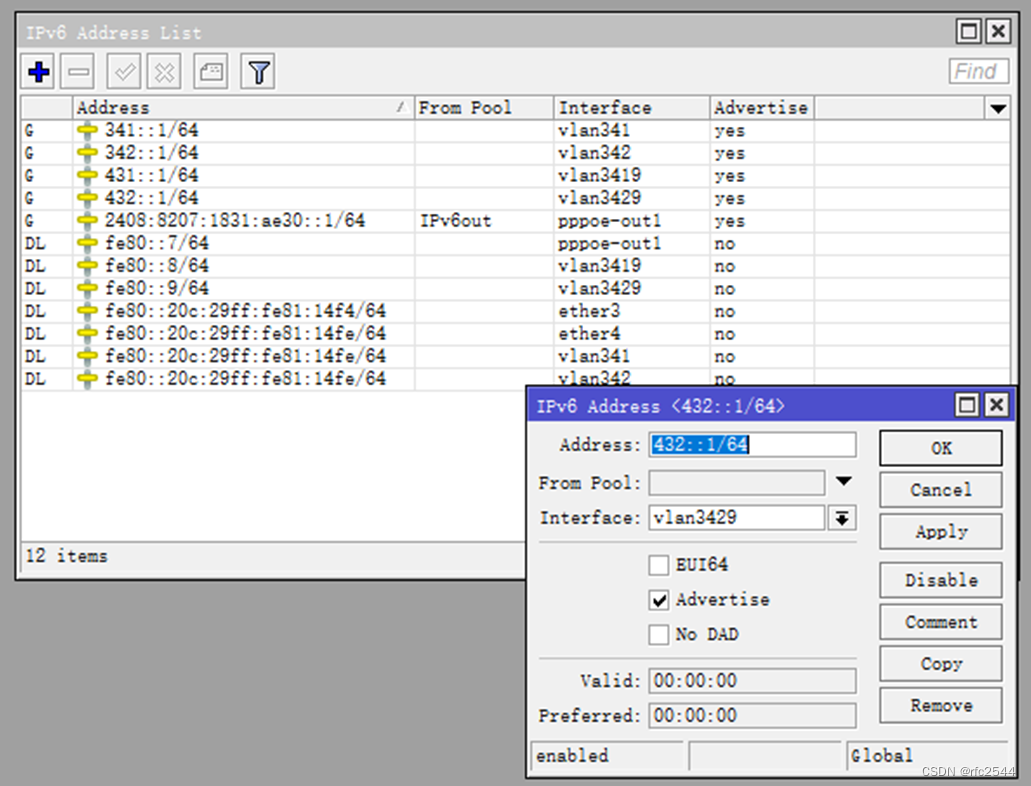
5.8.4 基于PPPoE的DHCPv6-PDserver
PD:给二级路由器的内网分配的前缀

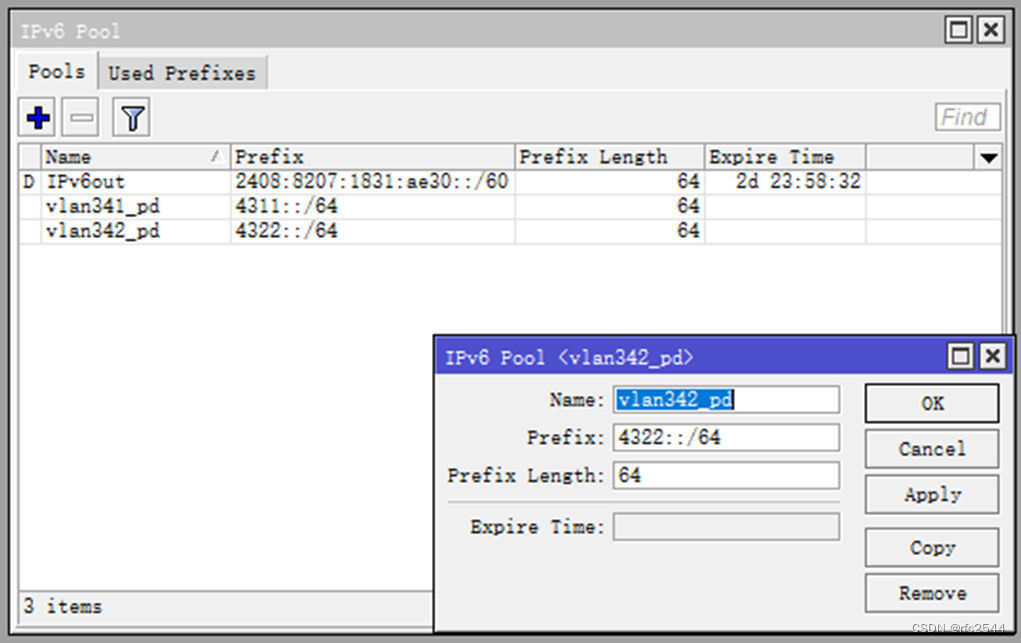
DNS server


DHCPv6-PD server

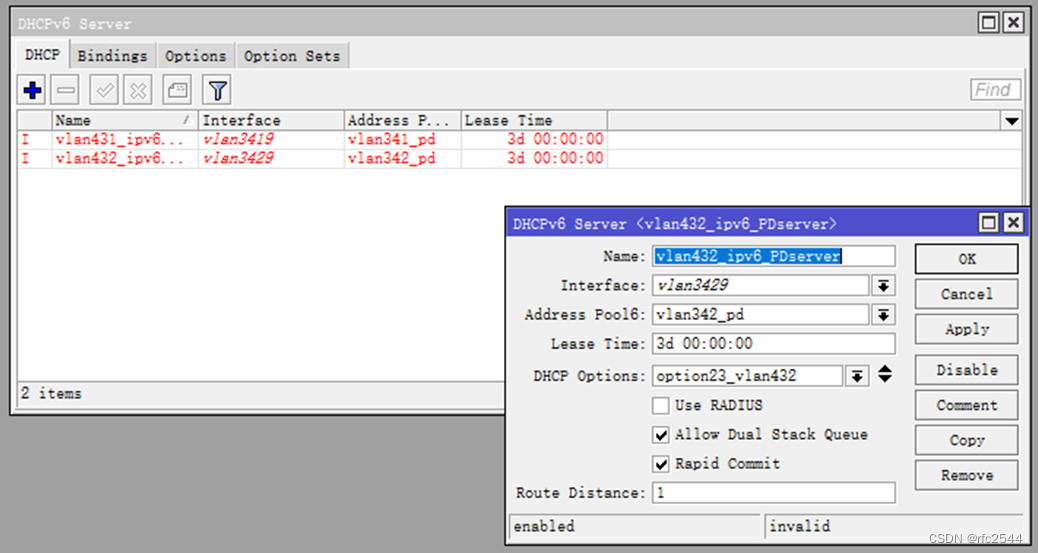
6 问题
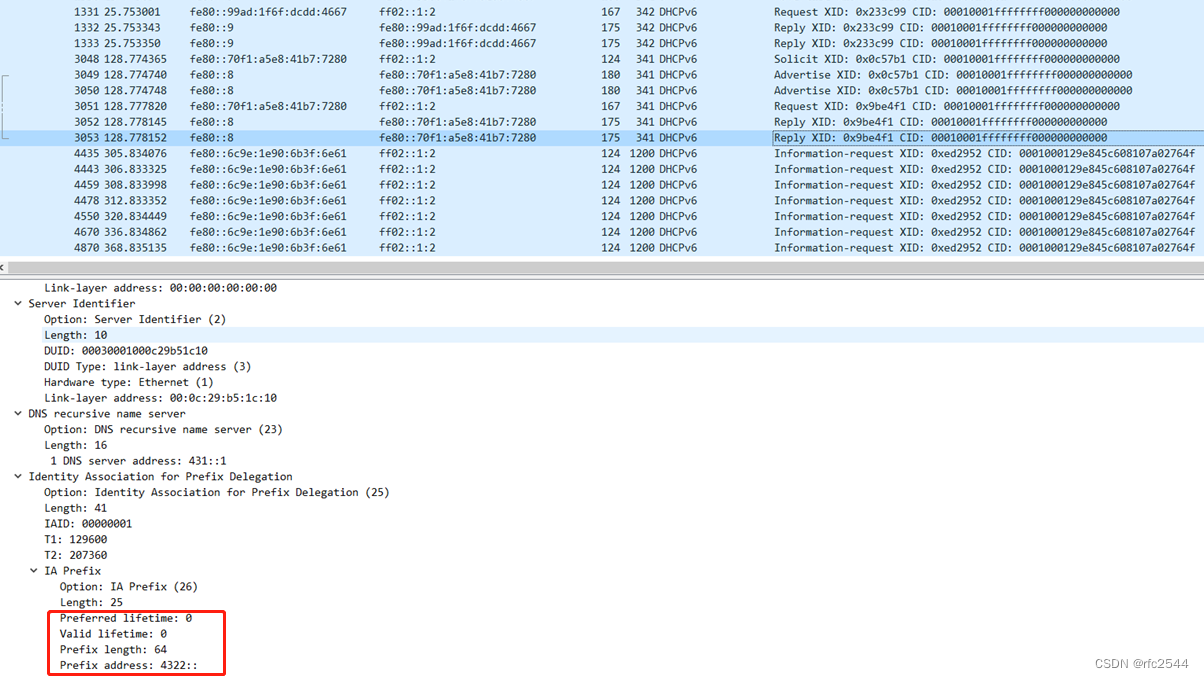
仅第一个拨号的二级路由器拿到的PD是对的,第二个拨号的二级路由器拿不到PD,抓包查看第二个路由器拨号的时候ROS dhcpv6给分配的PD仍是第一个拨号的二级路由器的PD且lifetime都是0,目前还未解决。

第一个拨号的二级路由器

第二个拨号的二级路由器