海洋馆的网站怎么做贵阳建站模板搭建
| 历年试题 |
| 2024年05月试题 BCN范式,模式分解,触发器类型 |
| 2023年05月试题 NoSQL基本特点,NoSQL对比,混合数据库 |
| 2022年05月试题4 两段锁,事务并发,数据一致,本地事务发布 |
| 2021年05月试题4 云数据库、数据库设计、看图填空 |
| 2020年11月试题4 索引过多缺点,物理分区,主从复制 |
| 2019年05月试题四 读写分离、主从复制,mxsgl,关系数据库和nosgl |
| 2018年05月试题四 视图,查询性能,数据不一致,触发器等 |
| 2017年05月试题2 数据库设计阶段,候选键,联系类型,范式 |
| 2017年05月试题4 反规范化技术,物理分区,水平垂直分区 |
| 2016年05月试题4 不规范化问题,并发操作,读写锁机制e |
| 2013年05月试题4 不规范化问题,反规范化优缺点,水平分割 |
| 2011年05月试题4 关系数据库和nsgl,ngsql存储类型,问题 |
| 2010年05月试题2 原型分析,分布式和集中数据库e |
| 2010年05月试题4 数据仓库,联邦数据库,数据集成方案判断 |
1.数据库体系结构

1.1 集中式数据库
1.1.1 三级模式

关系的3中类型
基本关系:通常又称为基本表或基表,实际存在的表,实际存储数据的逻辑表示。
查询表:查询结果对应的表。
视图表:由基本表或其他视图表导出的表,本身不是独立存储,数据库值存放它的定义,常称为虚表
视图
概念
它是一个虚拟表(逻辑上的表),其内容由查询定义(仅保存SQL查询语句),它是从一个表或多个表(或视图)导出的表。
同真实的表一样,视图包含一系列带有名称的列和行数据。但是视图并没有真正存储这些数据,而是通过查询原始表动态生成所需要的数据。在对视图的数据进行操作时,系统根据视图的定义去操作与视图相关联的基本表。
优点
- 视图能简化用户操作;
- 视图使用户能以多种角度看待同一数据;
- 视图对重构数据库提供了一定程度的逻辑独立性;
- 视图可以对机密的数据提供安全的保护。
物化视图
1)概念
它不是传统意义上的虚拟视图,是实体化视图,其本身会存储数据。同时当原始表中的数据更新时,物化视图也会更新。
物化视图是包括一个查询结果的数据库对象,它是远程数据的的本地副本,或者用来生成基于数据表求和的汇总表。
物化视图存储基于远程表的数据,也可以称为快照(类似于MYSQL Server中的snapshot,静态快照) 。
对于复制,物化视图允许你在本地维护远程数据的副本,这些副本是只读的。
如果你想修改本地副本,必须用高级复制的功能。
当你想从一个表或视图中抽取数据时,你可以用从物化视图中抽取。
对于数据仓库,创建的物化视图通常情况下是聚合视图,单一表聚合视图和连接视图。
物化视图,说白了,就是物理表,只不过这张表通过oracle的内部机制可以定期更新,将一些大的耗时的表连接用物化视图实现,会提高查询的效率。当然要打开查询重写选项;
2)物化视图和视图的区别
物化视图和视图类似,反映的是某个查询的结果,
但是和视图仅保存SQL定义不同,物化视图本身会存储数据,因此是物化了的视图。
1.2 分布式数据库

特点
数据独立性。除了数据的逻辑独立性与物理独立性外,还有数据分布独立性(分布透明性)。
集中与自治共享结合的控制结构。各局部的DBMS可以独立地管理局部数据库,具有自治的功能。同时,系统又设有集中的控制机制,协调各局部DBMS的工作,执行全局应用。
适当增加数据冗余度。
在不同的场地存储统一数据的多个副本,可以提高系统的可靠性和可用性,同时也提高系统性能。
提高系统的可用性,即当系统中某个节点发生故障时,因为数据有其他副本在非故障场地上,对其他所有场地来说,数据仍然时可用的,从而保证数据的完备性。
透明性分类

2. 数据库设计过程


需求分析
需求分析:通过调查研究,了解用户的数据和处理要求,并按一定格式整理形成需求说明书。产出物有 数据流图、数据字典、需求规格说明书
概念设计
概念设计:在需求分析阶段产生的需求说明书的基础上,按照特定的方法将它们抽象为一个不依赖于任何数据库管理系统的数据模型,即概念模型(ER模型:实体、联系、属性、扩展的ER模型)。

数据模型

关系模型相关概念
目或度:关系模式中属性的个数
候选码(候选键)
主码(主键)
主属性与非主属性:组成候选码的属性就是主属性,其他的就是非主属性。
外码(外键):其他关系的主键
全码(ALL-Key):关系模式的所有属性组是这个关系的候选码。
完整性约束
实体完整性约束:规定基本关系的主属性不能取空值
参照完整性约束:关系与关系间的引用,其他关系的主键或空值
用户自定义完整性约束:应用环境决定
触发器
逻辑设计
逻辑设计:将概念模型转化为某个特定的数据库管理系统上的逻辑模型。设计逻辑结构时,首先为概念模型选定一个合适的逻辑模型(通常是关系模型),然后将其转化为由特定DBMS支持的逻辑模型,最后对逻辑模型进行优化。

逻辑结构设计
- 一个实体必须转换为一个关系模式
- 联系转关系模式:一对一,一对多,多对多

物理设计
物理设计:对给定的逻辑模型选取一个最适合应用环境的物理结构,所谓数据库的物理结构,主要是指数据库在物理设备上的存储结构和存取方法。
3. 规范化理论

思考:范式级别提升带来了什么负面影响?
函数依赖
定义:设 R(U) 是属性集合 U={ A1, A2, … , An } 上的一个关系模式,X, Y 是 U 上的两个子集,若对 R(U) 的任意一个可能的关系 r ,r 中不可能有两个元组满足在 X 中的属性值相等而在 Y 中的属性值不等,则称 “ X 函数决定 Y ” 或 “ Y函数依赖于X ” ,记作 X → Y 。
键

Armstrong公理

范式

模式分解
无损分解

保持函数依赖

4. 反规范化
| 技术手段 | 说明 |
| 增加派生性列 | 增加派生列指增加的列可以通过表中其他数据计算生成。它的作用是在查询时减少计算量,从而加快查询速度。 例如:已有“单价”和“数量”列,增加“总价”列 |
| 增加冗余列 | 重新组表指如果许多用户需要查看两个表连接出来的结果数据,则把这两个表重新组成一个表来减少连接而提高性能。 |
| 重新组表 | 重新组表指如果许多用户需要查看两个表连接出来的结果数据,则把这两个表重新组成一个表来减少连接而提高性能。 |
| 分割表 | 水平分割,按记录进行分割,把数据放到多个独立的表中,主要用于表数据规模很大或表中数据相对独立或数据需要存放到多个介质上时使用。 垂直分割,对表进行分割,将主键与部分列放到一个表中,主键与其它列放到另一个表中, 在查询时减少 I/0 次数。 |
反规范化的优点
- 连接操作少,检索快、统计快。
- 需要查的表减少,检索容易。
反规范化的缺点
- 数据冗余,需要更大存储空间 (无解)
- 插入、更新、删除操作开销更大 (无解)
- 数据不一致,可能产生添加、修改、删除异常。可借助触发器数据同步,应用程序数据同步,物化视图解决。
- 更新和插入代码更难写 (无解)
5. 数据库功能控制

5.1 数据库安全性

5.2 并发控制
5.2.1 事务的ACID特性

5.2.2 并发产生的问题

5.2.3 并发问题解决方案

5.2.4 封锁协议
一级封锁协议。事务T在修改数据R之前必须先对其加X锁,直到事务结束才释放。可防止丢失修改
二级封锁协议。一级封锁协议加上事务T在读取数据R之前先对其加S锁,读完后即可释放S锁。可防止丢失修改,还可防止读“脏”数据
三级封锁协议。一级封锁协议加上事务T在读取数据R之前先对其加S锁,直到事务结束才释放。可防止丢失修改、防止读“脏”数据与防止数据(不可)重复读
两段锁协议。可串行化的。可能发生死锁
5.3 数据备份
- 冷备份也称为静态备份,是将数据库正常关闭,在停止状态下,将数据库的文件全部备份(复制)下来。
- 热备份也称为动态备份,是利用备份软件,在数据库正常运行的状态下,将数据库中的数据文件备份出来。
完全备份:备份所有数据
差量备份:仅备份上一次完全备份之后变化的数据
增量备份:备份上一次备份之后变化的数据
5.4 数据库故障与恢复

6. 数据库性能优化

6.1 集中式数据库性能优化
硬件升级:处理器、内存、磁盘子系统和网络。
数据库设计:反规范化技术(逻辑)、数据库分区(物理)。
索引优化策略
选择经常查询不常更新的属性、数据量小的不设置索引等。
查询优化
建立物化视图或尽可能减少多表查询等。
SQL优化
- 以不相干的子查询替代相干子查询
- 只检索需要的列(避免select *)
- 用带IN的条件子句等价替换OR子句
- 经常提交COMMIT,以尽早释放锁
- 尽可能减少多表查询
- 让自然连接和笛卡尔积运算的子表尽可能小
6.2 分布式数据库性能优化
主从复制、读写分离
数据库分片(分表)、分库
分布式缓存技术
分区分表分库

| 分区 | 分表 | |
| 共性 | 1.都针对数据表 2.都使用了分布式存储 3.都提升了查询效率 4.都降低了数据库的频繁I/O压力 | |
| 差异 | 逻辑上还是一张表 | 逻辑上已是多张表 |
分区技术
分区并不是生成新的数据表,而是将表的数据均衡分摊到不同的硬盘,系统或是不同服务器存储介质中,实际上还是一张表。
使用分区技术的优点:
减少维护工作量。独立管理每个分区比管理单张大表要轻松得多。
增强数据库的可用性。如果表的一个或几个分区由于系统故障而不能被使用,那么表其余的分区仍然可以使用;如果系统故障只影响表的一部分分区,那么,只有这部分分区需要修复,这就比修复整张大表耗费的时间少许多。
均衡I/O,减少竞争。通过把表的不同分区分配到不同的磁盘来平衡I/O改善性能。分区对用户保持透明。最终用户感觉不到分区的存在。
提高查询速度。对大表的查询、增加、修改等操作可以分解到表的不同分区中来并行执行。
数据分区技术一般分为水平分区和垂直分区,数据库中常见的是水平分区。
水平分区分为范围分区、哈希分区、列表分区等。

| 分区策略 | 分区方式 | 说明 |
| 范围分区 【RANGE】 | 按数据范围值来做分区 | 例:按用户编号分区,0-999999映射到分区A1000000-1999999映射到分区B. |
| 哈希分区 【HASH】 | 通过对key进行hash运算分区 | 例:可以把数据分配到不同分区,这类似于取余操作,余数相同的,放在一个分区上。 |
| 列表分区 【LIST】 | 根据某字段的某个具体值进行分区 | 例:长沙用户分成一个区,北京用户一个区。 |
| 范围分区 | 哈希分区 | 列表分区 | |
| 数据值 | 连续 | 连续、离散均可 | 离散 |
| 数据管理能力 | 强 | 弱 | 强 |
| 实施难度与可维护性 | 差 | 好 | 差 |
| 数据分布 | 不均匀 | 均匀 | 不均匀 |
分区的优点
1、相对于单个文件系统或是硬盘,分区可以存储更多的数据。
2、数据管理比较方便,比如要清理或废弃某年的数据,就可以直接删除该日期的分区数据即可
3、精准定位分区查询数据,不需要全表扫描查询,大大提高数据检索效率。
4、可跨多个分区磁盘查询,来提高查询的吞吐量。
5、在涉及聚合函数查询时,可以很容易进行数据的合并。
数据库主从复制
一般:一主多从,也可以多主多从。
主库做写操作,从库做读操作。
主从复制步骤:
主库(Master)更新数据完成前,将操作写binlog日志文件。
从库(Salve)打开I/O线程与主库连接,做binlog dump process,并将事件写入中继日志。
从库执行中继日志事件,保持与主库一致。
7. NoSQL非关系型数据库
NoSQL,Not-only SQL,泛指非关系型数据库。
| NoSQL的使用场景 | NoSQL的缺点不足 |
| 1 数据模型比较简单 2 需要灵活性更强的IT系统 3 对数据库性能要求较高 4 不需要高度的数据一致性 5 对于给定key容易映射复杂值的环境 | 1 成熟度不够,大量关键特征有待实现 2 开源数据库产品的支持力度有限 3 数据挖掘与商务智能支持不足 4 现有的产品无法直接使用NoSQL 5 擅长NoSQL的专家较少 |
7.1 与关系型数据库对比
| 特征 | 关系数据库模式 | NoSQL 模式 |
| 并发支持 | 支持并发、效率低 | 并发性能高 |
| 存储与查询 | 关系表方式存储、SQL 查询 | 海量数据存储、查询效率高 |
| 扩展方式 | 向上扩展 | 向外扩展 |
| 索引方式 | B树、哈希等 | 键值索引 |
| 应用领域 | 面向通用领域 | 特定应用领域 |
| 数据一致性 | 实时一致性 | 弱一致性 |
| 数据类型 | 结构化数据 | 非结构化 |
| 事物 | 高事务性 | 弱事务性 |
| 水平扩展 | 弱 | 强 |
| 数据容量 | 有限数据 | 海量数据 |
| 成本 | 花费巨大,成本高 | 部署简单,成本低,开源 |
| 查询速度 | 数据存储于硬盘中,SQL查询慢 | 数据存储于缓存中,查询速度快 |
| 存储数据类型 | 只支持基础数据类型,结构化 | 支持基础和对象,集合等非结构化类型 |
| 持久存储 | 支持海量数据存储 | 数据在缓存中,不适用于持久存储 |
7.2 NoSQL数据库的种类


键值Key - Value
键可是一个字符串对象,值可以是任意类型的数据。如整型、字符型、数组、列表、集合等。

列族数据库
分行式存储和列式存储。

文档数据库

图形数据库

8.缓存技术-Redis
常见缓存技术:
MemCache:Memcache是一个高性能的分布式的内存对象缓存系统,用于动态Web应用以减轻数据库负载。Memcache通过在内存里维护一个统一的巨大的hash表,它能够用来存储各种格式的数据,包括图像、视频、文件以及数据库检索的结果等。
Redis:Redis是一个开源的使用ANSIC语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的APl。
Squid:squid是一个高性能的代理缓存服务器,Squid支持FTP、gopher、HTTPS和HTTP协议。
思考:数据库与缓存数据是否有可能不一致?如何解决?
8.1 Redis数据类型
| 类型 | 特点 | 示例 |
| String 字符串 | 存储二进制,任何类型数据,最大512MB | 缓存,计数,共享Session |
| Hash 字典 | 无序字典,数组+链表,适合存对象 Key对应一个HashMap,针对一组数据 | 存储、读取、修改用户属性 |
| List 列表 | 双向链表,有序,增删快,查询慢 | 消息队列,文章列表 记录前N个最新登录的用户ID列表 |
| Set 集合 | 键值对无序,唯一 | 支持交/并/差集操作 独立IP,共同爱好,标签 |
| Sorted Set [Zset] 有序集合 | 键值对有序,唯一,自带按权重排序效果 | 排行榜 |
Redis新的3种数据类型:
Bitmaps,位操作字符串
HyperLoglog
Geographic
8.2 持久化RDB和AOF
RDB:传统数据库中快照的思想。指定时间间隔将数据进行快照存储。
AOF:传统数据库中日志的思想,把每条改变数据集的命令追加到AOF文件末尾,这样出问题了,可以重新执行AOF文件中的命令来重建数据集。
| 对比 | RDB | AOF |
| 备份量 | 重量级的全量备份,保存整个数据库 | 轻量级增量备份,一次只保存一个修改命令 |
| 保存间隔时间 | 保存间隔时间长 | 保存间隔时间短,默认1秒 |
| 还原速度 | 数据还原速度快 | 数据还原速度慢 |
| 阻塞情况 | save会阻塞,但bgsave或者自动不会阻塞 | 无论是平时还是AOD重写,都不会阻塞 |
| 数据体积 | 同等数据体积:小 | 同等数据体积:大 |
| 安全性 | 数据安全性:低,容易丢数据 | 数据安全性:高,根据策略决定 |
8.3 淘汰与过期策略
| 淘汰作用范围 | 机制名 | 策略 |
| 不淘汰 | noeviction | 禁止驱逐数据,内存不足以容纳新入数据时,新写入操作就会报错。系统默认的一种淘汰策略。 |
| 设置了过期时间的键空间 | volatile-random | 随机移除某个key |
| volatile-lru | 优先移除最近未使用的key | |
| volatile-ttl | ttl值小的key优先移除 | |
| 全键空间 | allkeys-random | 随机移除某个key |
| allkeys-lru | 优先移除最近未使用的key |
8.4 Redis与Memcache对比
| Memcache | Redis | |
| 数据类型 | 简单的Key-Value结构 | 丰富的数据结构 |
| 持久性 | 不支持 | 支持 |
| 分布式存储 | 客户端哈希分片/一致性哈希 | 多种方式,主从,Sentinel,Cluster等 |
| 多线程支持 | 支持 | Redis6.0开始支持 |
| 内存管理 | 私有内存池/内存池 | 无 |
| 事务支持 | 不支持 | 有限支持 |
| 数据容灾 | 不支持,不能做数据恢复 | 支持,可以在做数据恢复 |
8.5 Redis分布式存储方案
| 分布式存储方案 | 核心特点 |
| 主从(Master/Slave)模式 | 一主多从,故障时手动切换 |
| 哨兵(Sentinel)模式 | 有哨兵的一主多从,主节点故障自动选择新的主节点 |
| 集群(Cluster)模式 | 分节点对等集群,分slots,不同slots的信息存储到不同节点 |

8.6 Redis集群切片方式
| 切片方式 | 核心特点 |
| 客户单分片 | 在客户端通过key的hash值对应到不同的服务器 |
| 中间件实现分片 | 在应用软件和Redis中间,例如:Twemproxy、Codis等,由中间件实现服务到后台Redis节点的路由分派 |
| 客户端服务端协作分片 | 客户端与服务端协作完成分片处理 |
8.7 Redis数据分片方案
| 方案 | 分片方式 | 说明 |
| 范围分片 | 按数据范围值来做分片 | 例:按用户编号分片,0-999999映射到实例A;1000000-1999999映射到实例B。 |
| 哈希分片 | 通过key进行hash运算分片 | 可以把数据分配到不同实例,这类似于取余操作,余数相同的,放在一个实例上。 |
| 一致性哈希分片 | 哈希分片的改进 | 利于扩展结点,可以有效解决重新分配节点带来的无法命中问题。 |
8.8 Redis常见问题
缓存雪崩(Cache Avalanche)
(大部分缓存失效,造成数据库崩溃。)
对于系统 A,假设每天高峰期每秒 5000 个请求,本来缓存在高峰期可以扛住每秒 4000 个请求,但是缓存机器意外发生了全盘宕机。缓存挂了,此时 1 秒 5000 个请求全部落数据库,数据库必然扛不住,它会报一下警,然后就挂了。此时,如果没有采用什么特别的方案来处理这个故障,DBA 很着急,重启数据库,但是数据库立马又被新的流量给打死了。

缓存雪崩的事前事中事后的解决方案如下:
- 事前:Redis 高可用,主从+哨兵,Redis cluster,避免全盘崩溃。
- 事中:本地 ehcache 缓存 + hystrix 限流&降级,避免 MySQL 被打死。
- 事后:Redis 持久化,一旦重启,自动从磁盘上加载数据,快速恢复缓存数据。
答题答案:
使用锁或队列,保证不会有大量的线程对数据库一次性进行读写,从而避免失效时大量的并发请求落到底层存储系统上。
为key设置不同的缓存失效时间,在固定的一个缓存时间的基础上 + 随机一个时间作为缓存失效时间。
二级缓存,设置一个有时间限制的缓存 + 一个无时间限制的缓存。避免大规模访问数据库。
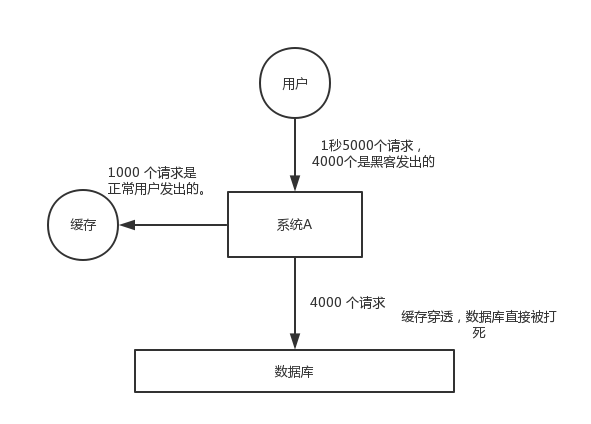
缓存穿透(Cache Penetration)
(查询无数据返回,直接查数据库。)
对于系统 A,假设一秒 5000 个请求,结果其中 4000 个请求是黑客发出的恶意攻击。
黑客发出的那 4000 个攻击,缓存中查不到,每次你去数据库里查,也查不到。
举个栗子。数据库 id 是从 1 开始的,结果黑客发过来的请求 id 全部都是负数。这样的话,缓存中不会有,请求每次都“视缓存于无物”,直接查询数据库。这种恶意攻击场景的缓存穿透就会直接把数据库给打死。
答题答案:
1.如果查询结果为空,直接设置一个默认值存放到缓存,这样第二次到缓冲中获取就有值了。设置一个不超过5分钟的过期时间,以便能正常更新缓存。
2.设置布隆过滤器,将所有可能存在的数据哈希到一个足够大的bitmap中,一个一定不存在的数据会被这个bitmap拦截掉,从而避免了对底层存储系统的查询压力。
布隆过滤器用于快速识别一个元素不在一个集合中,通过一个长二进制向量和一系列随机映射函数来记录与识别某个数据是否在一个集合中。

存击穿(Hotspot Invalid)
缓存击穿,就是说某个 key 非常热点,访问非常频繁,处于集中式高并发访问的情况,当这个 key 在失效的瞬间,大量的请求就击穿了缓存,直接请求数据库,就像是在一道屏障上凿开了一个洞。
不同场景下的解决方式可如下:
- 若缓存的数据是基本不会发生更新的,则可尝试将该热点数据设置为永不过期。
- 若缓存的数据更新不频繁,且缓存刷新的整个流程耗时较少的情况下,则可以采用基于 Redis、zookeeper 等分布式中间件的分布式互斥锁,或者本地互斥锁以保证仅少量的请求能请求数据库并重新构建缓存,其余线程则在锁释放后能访问到新缓存。
- 若缓存的数据更新频繁或者在缓存刷新的流程耗时较长的情况下,可以利用定时线程在缓存过期前主动地重新构建缓存或者延后缓存的过期时间,以保证所有的请求能一直访问到对应的缓存。
缓存预热
系统上线后,将相关需要缓存的数据直接加到缓存系统中。
解决:
- 直接写个缓存刷新页面,上线时手工操作。
- 数据量不大时,可以在项目启动的时候自动进行加载。
- 定时刷新缓存。
- 布隆过滤器用于快速识别一个元素不在一个集合中,通过一个长二进制向量和一系列随机映射函数来记录与识别某个数据是否在一个集合中。
缓存更新
除Redis系统自带的缓存失效策略,常见采用以下两种:
定时清理过期的缓存。
当有用户请求过来时,再判断这个请求所用到的缓存是否过期,过期的话就去底层系统得到新数据并更新缓存。
缓存降级
降级的目的是保证核心服务可用,即使是有损的,而且有些服务是无法降级的(如电商的购物流程等)。
在进行降级之前要对系统进行梳理,从而梳理出哪些必须保护,哪些可降级。
Redis相关资料
Redis概述与安装
https://blog.csdn.net/lili40342/article/details/127852124
Redis的5大数据类型
https://blog.csdn.net/lili40342/article/details/127897689
Redis的发布和订阅
https://blog.csdn.net/lili40342/article/details/127901009
Redis新的3种数据类型
https://blog.csdn.net/lili40342/article/details/127903901
Jedis操作Redis6
https://blog.csdn.net/lili40342/article/details/127904568
SpringBoot2整合Redis
https://blog.csdn.net/lili40342/article/details/127915177
Redis事务操作
https://blog.csdn.net/lili40342/article/details/127915924
Redis持久化之RDB(Redis DataBase)
https://blog.csdn.net/lili40342/article/details/127938199
Redis持久化之AOF(Append Only File)
https://blog.csdn.net/lili40342/article/details/127938233
Redis主从复制
https://blog.csdn.net/lili40342/article/details/127942076
Redis哨兵(Sentinel)
https://blog.csdn.net/lili40342/article/details/127942838
Redis集群(Cluster)
https://blog.csdn.net/lili40342/article/details/127942123
Redis应用问题解决(缓存穿透、击穿、雪崩、分布式锁)
https://blog.csdn.net/lili40342/article/details/127942407
9. 大数据

参考
https://blog.csdn.net/lili40342/article/details/128706099
