传统pc网站免费直播软件下载
目录
一、前言
二、源码分析
三、负载均衡策略
一、前言
如下图,我们在 orderserver 中通过 restTemplate 向 usersever 发起 http 请求,在服务拉取的时候,主机名 localhost 是用服务名 userserver 代替的,那么该 url 是一个可访问的网络地址吗?

我们在浏览器中访问一下这个地址,果然不可用。

那么它又是怎么访问到 userserver 数据的?别忘了我们的服务都是注册在 Eureka 上的,那肯定是拿着服务名去找 Eureka 要人了对不对?找到服务之后把具体的主机名替换掉就OK了。
实际上,我们可能有多个 userserver 同时注册在 Eureka 上,这时候 orderserver 要去 Eureka 上拉取服务的时候,拉取到的就不只是一个 userserver 服务了,它应该是一个服务列表,那么最终执行的时候肯定是只交给一个服务去做,到底要交给谁呢?没错,这就是我们本篇要说的 —— Ribbon,用它来实现多服务的负载均衡。
二、源码分析
上一篇文章中,提到了 @LoadBalanced 注解,我们说用它可以开启负载均衡。这个注解其实就是一个标记,标记 RestTemplate 发起的请求要被 Ribbon 拦截并处理。

那个这个拦截动作具体是谁来做的呢?Ctrl + Shift + N,搜索 LoadBalancerInterceptor,点击第一个。


我们可以打断点 debug,可以看到 request.getURI() 这一步是在获取请求路径,也就是我们上面说的那个不可用的 url。
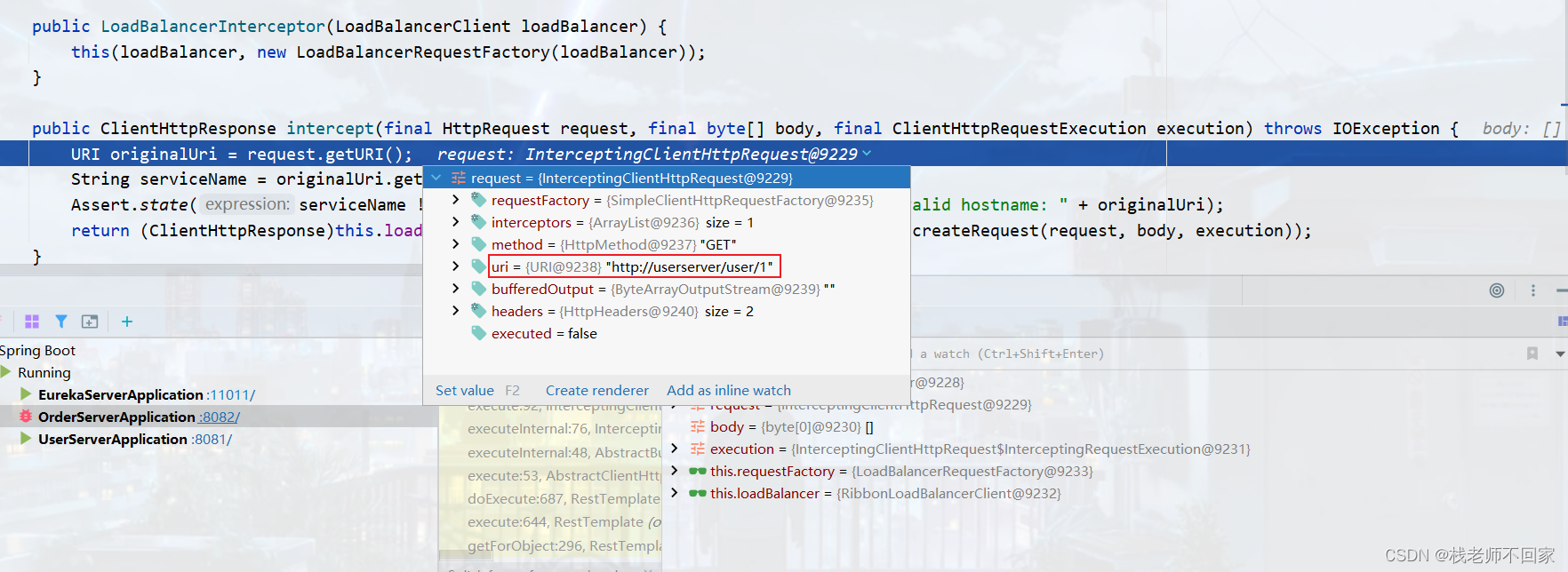
F8 快捷键下一步,originalUri.getHost() 应该就是在获取主机名,获取到的 host 正是 userserver。

拿到了主机名,就该去找 Eureka 拉取服务了,继续往下走,发现它把该服务名称交给了 loadBalancer.execute 去执行,F7 跟进该方法。

服务列表拿到之后就准备负载均衡了,F7 进入方法内部,我们发现它调用了 chooseServer 方法,翻译一下:选择服务。从刚才拉取到的服务列表中选择一个出来?

继续 F7 进入 chooseServer 方法,可以看到它又去调用父类的 chooseServer 方法了。

跟进方法往下走,返回一个 rule.choose?翻译一下:选择规则。说明我们从服务列表中选择一个服务的时候也是有规则的。

光标放到 rule 上,Ctrl 加鼠标左键跟进,它原来是一个 IRule 类型的。

那么这个 IRule 接口有哪些具体的 Rule 呢?光标放在 IRule 上,Ctrl + H,弹出它的实现类。翻译一下:有随机规则、轮询规则等等。
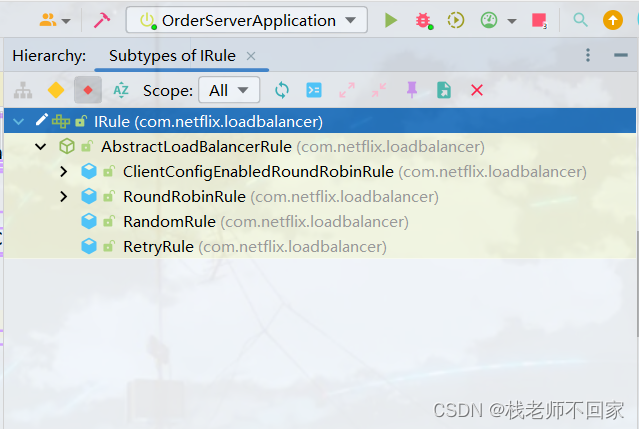
拿到了真实的访问地址,并且选择了一种负载均衡策略,就可以对之前不可访问的 url 进行替换了。
整体流程:
orderserver 发起 http 请求 → 请求被 LoadBalancerInterceptor 负载均衡拦截器拦截 → RibbonLoadBalancerClient 拿到服务名,并将其作为参数传给 DynamicServerListLoadBalancer → DynamicServerListLoadBalancer 就会去 Eureka 中拉取服务列表 → 随后 DynamicServerListLoadBalancer 又会去请求 IRule 接口做负载均衡,根据规则挑一个服务出来,并返回 → RibbonLoadBalancerClient 拿到了真实的服务地址就会对之前不可访问的 url 地址进行替换,最终请求到目标服务。
三、负载均衡策略
如下图,每一个子接口都是一种规则:
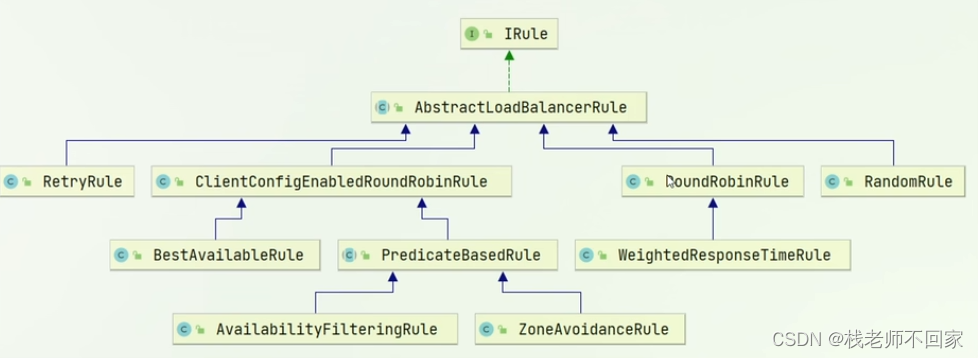

默认是的负载均衡策略是 ZoneAvoidanceRule,它父类的父类是轮询的,所以本质上讲 ZoneAvoidanceRule 也是一个轮询策略,但是它是以 Zone 对服务器进行划分的,这个 Zone 可以理解为一个机房,所以在选择服务的时候,它会优先选择跟自己在同一个机房里面的服务,然后进行轮询。
那么如何修改负载均衡规则呢?有两种方式。
① 代码方式,在 orderserver 的启动类中定义一个新的 IRule(作用于全局)
@Bean
public IRule randomRule() {return new RandomRule();
}② 配置文件方式,在 orderserver 的 yml 文件中添加新的配置(只针对某个微服务而言)

Ribbon 的默认加载机制是懒加载,所谓懒加载就是不用的时候不加载,什么时候要用了才去加载,所以服务在第一次被访问的时候速度较慢,由于 Ribbon 给我们提供了缓存,所以之后的访问速度还是很快的。
相对于懒加载的是饥饿加载,顾名思义,饥饿加载就是在项目一启动的时候就开始加载,所以它的每一次访问速度都很快。那么如何修改 Ribbon 的加载方式呢?我们可以通过配置文件的方式进行修改。

