高端品牌网站建设内容站长工具seo综合查询全面解析
目录:
- 学习目标
- 认识Pandas中的数据结构和数据类型
- Series对象
- 通过numpy.ndarray数组来创建
- 通过list列表来创建
- 使用字典或元组创建s对象
- 在notebook中不写print
- Series对象常用API
- 布尔值列表获取Series对象中部分数据
- Series对象的运算
- DataFrame对象
- 创建df对象
- DataFrame对象常用API
- 布尔值列表获取df对象中部分数据
- 根据df对象的判断表达式返回自定义的值
- df对象的运算
- Pandas的数据类型初识
- 总结
- 项目地址
1.学习目标
-
知道什么是DataFrame对象、什么是Seires对象
-
对Series和DataFrame的常用API有印象、能找到、能看懂
-
了解Pandas中常用数据类型
-
知道Series以及DataFrame的运算规则
2.认识Pandas中的数据结构和数据类型
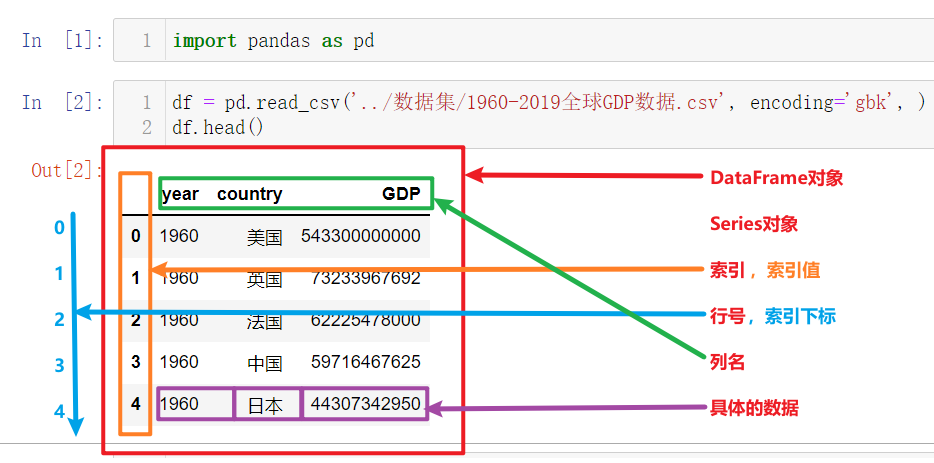
上图为上一节中读取并展示出来的数据,以此为例我们来讲解Pandas的核心概念,以及这些概念的层级关系:
DataFrame
Series
索引列
索引名、索引值
索引下标、行号
数据列
列名
列值,具体的数据
其中最核心的就是Pandas中的两个数据结构:DataFrame和Series
3.Series对象
-
Series也是Pandas中的最基本的数据结构对象,下文中简称s对象;是DataFrame的列对象或者行对象,series本身也具有索引。
-
Series是一种类似于一维数组的对象,由下面两个部分组成:
-
values:一组数据(numpy.ndarray类型)
-
index:相关的数据索引标签;如果没有为数据指定索引,于是会自动创建一个0到N-1(N为数据的长度)的整数型索引。
-
4.通过numpy.ndarray数组来创建
import numpy as np
import pandas as pd# 自动生成索引
# 创建numpy.ndarray对象
# array([1, 2, 3])
# print打印输出 [1 2 3]
# type()为<class 'numpy.ndarray'>
n1 = np.array([1, 2, 3])
print(n1)
print(type(n1))# 创建Series对象
# type()为<class 'pandas.core.series.Series'>
s1 = pd.Series(n1)
print(s1)
print(type(s1))# 创建Series对象,同时指定索引
# type()为<class 'pandas.core.series.Series'>
s1 = pd.Series(n1, index=['A', 'B', 'C'])
print(s1)
print(type(s1))5.通过list列表来创建
import pandas as pd# 使用默认自增索引
s2 = pd.Series([1, 2, 3])
print(s2)
# 自定义索引
s3 = pd.Series([1, 2, 3], index=['A', 'B', 'C'])
print(s3)6.使用字典或元组创建s对象
import pandas as pd# 使用元组
tst = (1, 2, 3, 4, 5, 6)
s1 = pd.Series(tst)
print(s1)
print(type(s1))# 使用字典:
dst = {'A': 1, 'B': 2, 'C': 3, 'D': 4, 'E': 5, 'F': 6}
s2 = pd.Series(dst)
print(s2)
print(type(s2))
7.在notebook中不写print
- 在JupyterNotebook中,默认只会打印输出最后出现的变量名;许多时候我们要写大量的print;通过下面的2行代码即可解决这个问题
import pandas as pd# 在notebook执行代码之前首先需要先执行下面代码以设置InteractiveShell.ast_node_interactivity参数
from IPython.core.interactiveshell import InteractiveShellInteractiveShell.ast_node_interactivity = 'all'
# 这个方法的作用范围仅限当前kernel(一个.ipynb文件对应一个kernel)
# 可以让我们在jupyternotebook中不用写print# 使用默认自增索引
s2 = pd.Series([1, 2, 3])
s2
# 自定义索引
s3 = pd.Series([1, 2, 3], index=['A', 'B', 'C'])
s3
8.Series对象常用API
import pandas as pd# 构造一个Series对象
s4 = pd.Series([i for i in range(6)], index=[i for i in 'ABCDEF'])
print(s4)# Series对象常用属性和方法# s对象有多少个值,int
print(len(s4))
print(s4.size)# s对象有多少个值,单一元素构成的元组 (6,)
print(s4.shape)# 查看s对象中数据的类型
print(s4.dtypes)# s对象转换为list列表
print(s4.to_list())# s对象的值 array([0, 1, 2, 3, 4, 5], dtype=int64)
print(s4.values)# s对象的值转换为列表
print(s4.values.tolist())# s对象可以遍历,返回每一个值
for i in s4:print(i)# 下标获取具体值
print(s4[1])# 返回前2个值,默认返回前5个
print(s4.head(2))# 返回最后1个值,默认返回后5个
print(s4.tail(1))# 获取s对象的索引 Index(['A', 'B', 'C', 'D', 'E', 'F'], dtype='object')
print(s4.index)# s对象的索引转换为列表
print(s4.index.to_list())# s对象中数据的基础统计信息
print(s4.describe())# 返回结果及说明如下
# count 6.000000 # s对象一共有多少个值
# mean 2.500000 # s对象所有值的算术平均值
# std 1.870829 # s对象所有值的标准偏差
# min 0.000000 # s对象所有值的最小值
# 25% 1.250000 # 四分位 1/4位点值
# 50% 2.500000 # 四分位 1/2位点值
# 75% 3.750000 # 四分位 3/4位点值
# max 5.000000 # s对象所有值的最大值
# dtype: float64
# 标准偏差是一种度量数据分布的分散程度之标准,用以衡量数据值偏离算术平均值的程度。标准偏差越小,这些值偏离平均值就越少,反之亦然。
# 四分位数(Quartile)也称四分位点,是指在统计学中把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值。# seriest对象转换为df对象
df = pd.DataFrame(s4)
print(df)
print(type(df))
9.布尔值列表获取Series对象中部分数据
import pandas as pds4 = pd.Series([i for i in range(6)], index=[i for i in 'ABCDEF'])# 构造布尔值构成的列表,元素数量和s对象的值数量相同
bool_list = [True]*3 + [False]*3
print(bool_list)# Series[[True, False, ...]]
print(s4[bool_list])
print(s4[[True, True, True, False, False, False]])
10.Series对象的运算
-
Series和数值型变量计算时,变量会与Series中的每个元素逐一进行计算
-
两个Series之间计算,索引值相同的元素之间会进行计算;索引不同的元素最终计算的结果会填充成缺失值,用NaN表示
import pandas as pds4 = pd.Series([i for i in range(6)], index=[i for i in 'ABCDEF'])# Series和数值型变量计算
print(s4 * 5)# 索引完全相同的两个Series对象进行计算
print(s4)
# 构造与s4索引相同的s对象
s5 = pd.Series([10] * 6, index=[i for i in 'ABCDEF'])
print(s5)
# 两个索引相同的s对象进行运算
print(s4 + s5)# 索引不同的两个s对象运算
print(s4)
# 注意s6的最后一个索引值和s4的最后一个索引值不同
s6 = pd.Series([10]*6, index=[i for i in 'ABCDEG'])
print(s6)
print(s4 + s6)11.DataFrame对象
- DataFrame是一个表格型的数据结构,它含有一组或多组有序的列(Series),每列可以是不同的值类型(数值、字符串、布尔值等)。
-
DataFrame是Pandas中的最基本的数据结构对象,简称df;可以认为df就是一个二维数据表,这个表有行有列有索引
-
DataFrame是Pandas中最基本的数据结构,Series数据对象的许多属性和方法在DataFrame中也一样适用
12.创建df对象
DataFrame的创建有很多种方式
-
Serires对象转换为df:上一小节中学习了
s.to_frame()以及s.reset_index() -
读取文件数据返回df:在之前的学习中我们使用了
pd.read_csv('csv格式数据文件路径')的方式获取了df对象 -
使用字典、列表、元组创建df:接下来就展示如何使用字段、列表、元组创建df
import pandas as pd# 使用字典加列表创建df,使默认自增索引
df1_data = {'日期': ['2021-08-21', '2021-08-22', '2021-08-23'],'温度': [25, 26, 50],'湿度': [81, 50, 56]
}
df1 = pd.DataFrame(data=df1_data)
print(df1)
print(type(df1))# 使用列表加元组创建df,并自定义索引
df2_data = [('2021-08-21', 25, 81),('2021-08-22', 26, 50),('2021-08-23', 27, 56)
]
df2 = pd.DataFrame(data=df2_data,columns=['日期', '温度', '湿度'],index=['row_1', 'row_2', 'row_3'] # 手动指定索引
)
print(df2)
print(type(df2))
13.DataFrame对象常用API
import pandas as pd# 使用列表加元组创建df,并自定义索引
df2_data = [('2021-08-21', 25, 81),('2021-08-22', 26, 50),('2021-08-23', 27, 56)
]
df2 = pd.DataFrame(data=df2_data,columns=['日期', '温度', '湿度'],index=['row_1', 'row_2', 'row_3'] # 手动指定索引
)# 返回df的行数
print(len(df2))# df中数据的个数
print(df2.size)# df中的行数和列数,元组 (行数, 列数)
print(df2.shape)# 返回列名和该列数据的类型
print(df2.dtypes)# 返回nparray类型的2维数组,每一行数据作为一维数组,所有行数据的数组再构成一个二维数组
print(df2.values)# 返回df的所有列名
print(df2.columns)# df遍历返回的只是列名
for col_name in df2:print(col_name)# 返回df的索引对象
print(df2.index)# 返回第一行数据,默认前5行
print(df2.head(1))# 返回倒数第1行数据,默认倒数5行
print(df2.tail(1))# 返回df的基本信息:索引情况,以及各列的名称、数据数量、数据类型
# series对象没有info()方法
print(df2.info())# 返回df对象中所有数字类型数据的基础统计信息
# 返回对象的内容和Series.describe()相同
print(df2.describe())# 返回df对象中全部列数据的基础统计信息
print(df2.describe(include='all'))
14.布尔值列表获取df对象中部分数据
import pandas as pd# 使用列表加元组创建df,并自定义索引
df2_data = [('2021-08-21', 25, 81),('2021-08-22', 26, 50),('2021-08-23', 27, 56)
]
df2 = pd.DataFrame(data=df2_data,columns=['日期', '温度', '湿度'],index=['row_1', 'row_2', 'row_3'] # 手动指定索引
)print(df2[[True, False, True]])
15.根据df对象的判断表达式返回自定义的值
import pandas as pd# 使用列表加元组创建df,并自定义索引
df2_data = [('2021-08-21', 25, 81),('2021-08-22', 26, 50),('2021-08-23', 27, 56)
]
df2 = pd.DataFrame(data=df2_data,columns=['日期', '温度', '湿度'],index=['row_1', 'row_2', 'row_3'] # 手动指定索引
)print(df2.index != 'row_2')
print(df2[df2.index != 'row_2'])
16.df对象的运算
-
当DataFrame和数值进行运算时,DataFrame中的每一个元素会分别和数值进行运算,但df中的数据存在非数值类型时不能做加减除法运算
-
两个DataFrame之间、以及df和s对象进行计算,和2个series计算一样,会根据索引的值进行对应计算:当两个对象的索引值不能对应时,不匹配的会返回NaN
import pandas as pddf1_data = {'日期': ['2021-08-21', '2021-08-22', '2021-08-23'],'温度': [25, 26, 50],'湿度': [81, 50, 56]
}
df1 = pd.DataFrame(data=df1_data)
print(df1)# 使用列表加元组创建df,并自定义索引
df2_data = [('2021-08-21', 25, 81),('2021-08-22', 26, 50),('2021-08-23', 27, 56)
]
df2 = pd.DataFrame(data=df2_data,columns=['日期', '温度', '湿度'],index=['row_1', 'row_2', 'row_3'] # 手动指定索引
)
print(df2)# 不报错
print(df2 * 2)
# 报错,因为df2中有str类型(Object)的数据列
# print(df2 + 1)# df和df进行运算
# 索引完全不匹配
print(df1 + df2)# 构造部分索引和df2相同的新df
df3 = df2[df2.index!='row_3']
print(df3)# 部分索引相同
print(df2 + df3)17.Pandas的数据类型初识
-
df或s对象中具体每一个值的数据类型有很多,如下表所示
| Pandas数据类型 | 说明 | 对应的Python类型 |
|---|---|---|
| Object | 字符串类型 | string |
| int | 整数类型 | int |
| float | 浮点数类型 | float |
| datetime | 日期时间类型 | datetime包中的datetime类型 |
| timedelta | 时间差类型 | datetime包中的timedelta类型 |
| category | 分类类型 | 无原生类型,可以自定义 |
| bool | 布尔类型 | True,False |
| nan | 空值类型 | None |
-
可以通过下列API查看s对象或df对象中数据的类型
s1.dtypes
df1.dtypes
df1.info() # s对象没有info()方法- `int64`后边的64表示所占字节数
18.总结
-
理解类知识点
-
dataframe和series对象是什么:
-
可以认为df是有行有列有索引的二维数据表
-
df和s是Pandas中最核心的数据结构
-
df中每一列或者每一行都是s对象
-
s对象也有索引
-
每一个s对象都有各自的数据类型,表示构成这个s对象中的值的type;常用的数据类型有
-
Object -- 字符串
-
int -- 整数
-
float -- 小数
-
-
-
series和dataframe的API
# <s/df>表示s对象或df对象
<s/df>.size # 返回数据个数
<s/df>.shape # s返回(行数,),df返回(行数,列数)
<s/df>.dtypes # s返回数据类型,df返回列名和该列数据的类型
<s/df>.values # 返回全部值
<s/df>.index # 查看索引
<s/df>.head() # s返回前5个数据,df返回前5行数据
<s/df>.tail() # s返回后5个数据,df返回后5行数据
df.info() # 返回df的基本信息:索引情况,以及各列的名称、数据数量、数据类型;s对象没有这个函数
<s/df>.describe() # 返回s或df对象中所有数值类型数据的基础统计信息
df.describe(include='all') # 返回df对象中全部列数据的基础统计信息series以及dataframe的运算
- 当s或df和数值进行运算时,每一个具体的值会分别和数值进行运算,但s或df中的数据存在非数值类型时不能做加减除法运算
- 两个s之间、两个df之间,以及df和s对象进行计算,会根据索引的值进行对应计算,当两个对象的索引值不能对应时,不匹配的会返回NaN
判断表达式
-
s对象的判断表达式返回由布尔值构成的numpy.ndarray数组
-
s > 0==>array([True, False, True]) -
df.index!='row_2'==>array([True, False, True])
-
-
布尔值列表或数组获取s或df对象中部分数据的方法:返回True对应的(行)数据
-
s[[True, True, True, False, False, False]]ors[s>0] -
df[[True, True, True, False, False, False]]ordf[df.index!='xxx']
-
19.项目地址
Python: 66666666666666 - Gitee.com
