泊头做网站的微信商店小程序制作教程
在当今竞争激烈的商业环境中,企业的人才战略对于其长期发展至关重要。为了有效实施人才战略,企业需要一套精准、高效的人才管理工具,而人才画像系统正是满足这一需求的关键解决方案。本文将探讨人才画像系统如何支撑企业的人才战略落地,从数据驱动的人才识别、个性化发展路径规划、以及优化人才配置等方面进行深入分析。
一、数据驱动的人才识别
1.多维度数据整合
人才画像系统通过整合来自不同渠道的数据,如员工基本信息、绩效评估、培训记录、职业兴趣等,构建全面的员工画像。这些数据不仅涵盖了员工的硬技能(如专业技能、工作经验),还包括了软技能(如团队合作能力、领导力、创新能力)和个性特质,为企业提供了全面、深入的人才洞察。
2.智能匹配与推荐
基于大数据分析和机器学习算法,人才画像系统能够智能识别员工的潜能和优势,并将其与企业的岗位需求、项目需求进行匹配。这不仅有助于企业快速找到最适合的人选,还能提高员工的满意度和忠诚度,因为员工被赋予了更符合其能力和兴趣的工作任务。
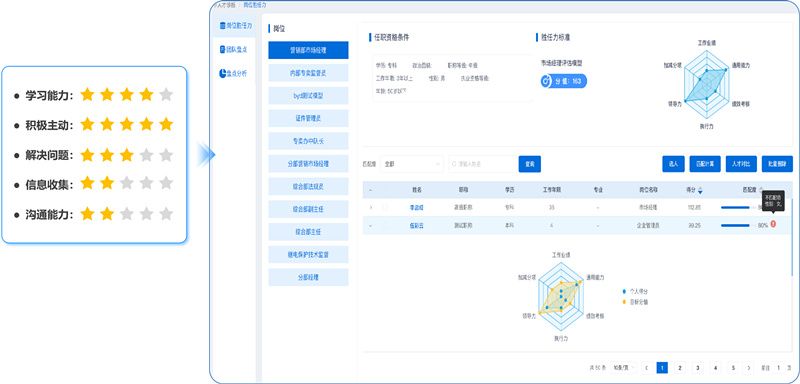
二、个性化发展路径规划
1.定制化培训与发展计划
人才画像系统能够分析员工的职业目标、技能缺口和发展需求,从而为企业和员工提供定制化的培训和发展计划。这些计划不仅关注员工的当前技能提升,还着眼于其未来职业发展的长期规划,帮助员工实现个人价值的同时,也促进了企业的人才梯队建设。
2.持续跟踪与反馈
系统还能持续跟踪员工的培训进度和职业发展情况,提供定期的反馈和评估。这有助于企业及时调整培训策略,确保员工的发展与企业的人才战略保持一致。同时,员工也能通过系统了解自己的成长轨迹,激发其自我提升的动力。
三、优化人才配置与决策支持
1.高效人才调配
人才画像系统使企业能够基于员工的技能和潜力,进行高效的人才调配。当企业面临项目变动、业务拓展等挑战时,系统能够快速识别并调配最适合的人才资源,确保项目的顺利进行和企业的持续发展。
2.数据驱动的决策支持
系统提供的数据分析和报告功能,为企业的人才决策提供了科学依据。无论是人才选拔、晋升、还是人才保留策略,企业都可以基于系统提供的数据洞察,做出更加明智、公正和有效的决策。
四、促进组织文化与人才战略的融合
1.强化组织认同感
人才画像系统通过展现员工的个性特质和职业兴趣,有助于企业更好地理解和尊重员工的多样性。这不仅增强了员工的归属感和组织认同感,还促进了企业文化的建设和传播,为人才战略的落地提供了良好的组织氛围。
2.持续迭代与优化
人才画像系统是一个持续迭代和优化的过程。随着企业的发展和员工的变化,系统需要不断更新和完善,以确保其始终能够精准反映企业的人才需求和员工的发展需求。这要求企业保持对系统的关注和投入,同时也为企业的持续改进和创新提供了动力。
人才画像系统通过数据驱动的人才识别、个性化发展路径规划、以及优化人才配置与决策支持等关键功能,为企业的人才战略落地提供了强有力的支撑。它不仅提高了企业的人才管理效率和质量,还促进了员工的个人成长和职业发展,为企业的长期发展奠定了坚实的基础。因此,企业应高度重视人才画像系统的建设和应用,将其作为实施人才战略的重要工具。
