电子商务网站建设研究杭州品牌网站设计
Redis持久化
Redis有两种持久化方案:
- RDB持久化
- AOF持久化
1.1.RDB持久化
RDB全称Redis Database Backup file(Redis数据备份文件),也被叫做Redis数据快照。简单来说就是把内存中的所有数据都记录到磁盘中。当Redis实例故障重启后,从磁盘读取快照文件,恢复数据。快照文件称为RDB文件,默认是保存在当前运行目录。
1.1.1.执行时机
RDB持久化在四种情况下会执行:
- 执行save命令
- 执行bgsave命令
- Redis停机时
- 触发RDB条件时
1)save命令
执行下面的命令,可以立即执行一次RDB:

save命令会导致主进程执行RDB,这个过程中其它所有命令都会被阻塞。只有在数据迁移时可能用到。
2)bgsave命令
下面的命令可以异步执行RDB:

这个命令执行后会开启独立进程完成RDB,主进程可以持续处理用户请求,不受影响。
3)停机时
Redis停机时会执行一次save命令,实现RDB持久化。
4)触发RDB条件
Redis内部有触发RDB的机制,可以在redis.conf文件中找到,格式如下:
# 900秒内,如果至少有1个key被修改,则执行bgsave , 如果是save "" 则表示禁用RDB
save 900 1
save 300 10
save 60 10000
RDB的其它配置也可以在redis.conf文件中设置:
# 是否压缩 ,建议不开启,压缩也会消耗cpu,磁盘的话不值钱
rdbcompression yes# RDB文件名称
dbfilename dump.rdb # 文件保存的路径目录
dir ./
1.1.2.RDB原理
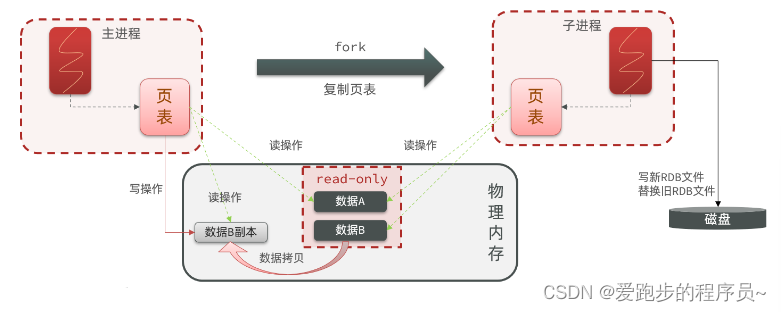
bgsave开始时会fork主进程得到子进程,子进程共享主进程的内存数据。完成fork后读取内存数据并写入 RDB 文件。
fork采用的是copy-on-write技术:
- 当主进程执行读操作时,访问共享内存;
- 当主进程执行写操作时,则会拷贝一份数据,执行写操作。
1.1.3.小结
RDB方式bgsave的基本流程?
- fork主进程得到一个子进程,共享内存空间
- 子进程读取内存数据并写入新的RDB文件
- 用新RDB文件替换旧的RDB文件
RDB会在什么时候执行?save 60 1000代表什么含义?
- 默认是服务停止时
- 代表60秒内至少执行1000次修改则触发RDB
RDB的缺点?
- RDB执行间隔时间长,两次RDB之间写入数据有丢失的风险
- fork子进程、压缩、写出RDB文件都比较耗时
1.2.AOF持久化
1.2.1.AOF原理
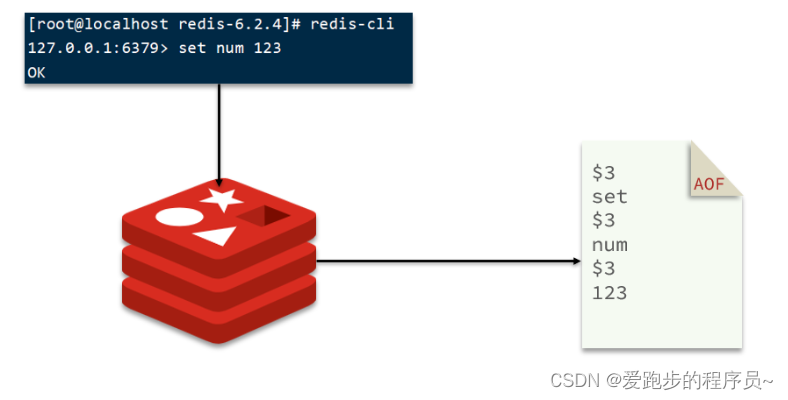
AOF全称为Append Only File(追加文件)。Redis处理的每一个写命令都会记录在AOF文件,可以看做是命令日志文件。
1.2.2.AOF配置
AOF默认是关闭的,需要修改redis.conf配置文件来开启AOF:
# 是否开启AOF功能,默认是no
appendonly yes
# AOF文件的名称
appendfilename "appendonly.aof"
AOF的命令记录的频率也可以通过redis.conf文件来配:
# 表示每执行一次写命令,立即记录到AOF文件
appendfsync always
# 写命令执行完先放入AOF缓冲区,然后表示每隔1秒将缓冲区数据写到AOF文件,是默认方案
appendfsync everysec
# 写命令执行完先放入AOF缓冲区,由操作系统决定何时将缓冲区内容写回磁盘
appendfsync no
三种策略对比:

1.2.3.AOF文件重写
因为是记录命令,AOF文件会比RDB文件大的多。而且AOF会记录对同一个key的多次写操作,但只有最后一次写操作才有意义。通过执行bgrewriteaof命令,可以让AOF文件执行重写功能,用最少的命令达到相同效果。

如图,AOF原本有三个命令,但是set num 123 和 set num 666都是对num的操作,第二次会覆盖第一次的值,因此第一个命令记录下来没有意义。
所以重写命令后,AOF文件内容就是:mset name jack num 666
Redis也会在触发阈值时自动去重写AOF文件。阈值也可以在redis.conf中配置:
# AOF文件比上次文件 增长超过多少百分比则触发重写
auto-aof-rewrite-percentage 100
# AOF文件体积最小多大以上才触发重写
auto-aof-rewrite-min-size 64mb
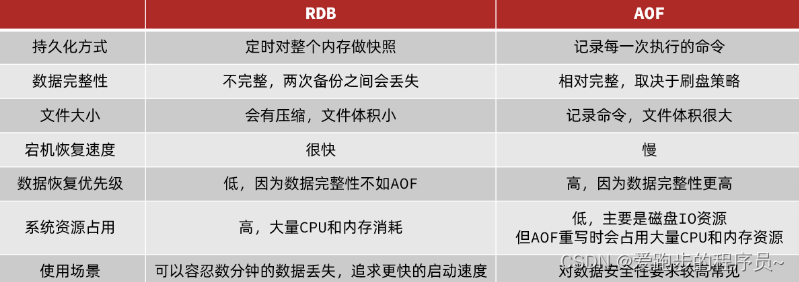
1.3.RDB与AOF对比
RDB和AOF各有自己的优缺点,如果对数据安全性要求较高,在实际开发中往往会结合两者来使用。
将RDB和AOF两种持久化方式结合使用,以提供更好的数据保护和恢复能力。在这种配置下,Redis服务器会根据你的设置同时生成RDB文件和AOF文件。当Redis服务器重启时,它会首先加载AOF文件来还原数据,如果AOF文件不存在或损坏,则会尝试加载RDB文件。
要在Redis中启用RDB和AOF持久化,你可以在Redis的配置文件中进行相应的设置。例如,你可以使用以下配置来启用RDB和AOF持久化:
save 900 1
save 300 10
save 60 10000
appendonly yes
这个配置表示在900秒内,如果至少有1个键被修改,则触发生成RDB文件;在300秒内,如果至少有10个键被修改,则触发生成RDB文件;在60秒内,如果至少有10000个键被修改,则触发生成RDB文件。同时, appendonly yes 表示启用AOF持久化。
使用RDB和AOF持久化可以提供更好的数据保护和恢复能力,但也会增加服务器的磁盘占用和IO负载。因此,在配置时需要根据具体需求权衡各种因素。
