单片机和做网站河南省企业年报网上申报入口
案例使用springboot项目,在IDEA 中集成Docker生成镜像,并将镜像发布到linux服务器
具体步骤如下:
1、Centos7安装Docker
更新系统的软件包列表
sudo yum update
安装Docker所需的软件包和依赖项:
sudo yum install docker
完成安装后,启动Docker服务。在终端中运行以下命令:
sudo service docker start
验证Docker是否成功安装。在终端中运行以下命令:
docker --version
linux查看docker运行状态:
systemctl status docker
2、Docker开启远程访问:
vim /lib/systemd/system/docker.service
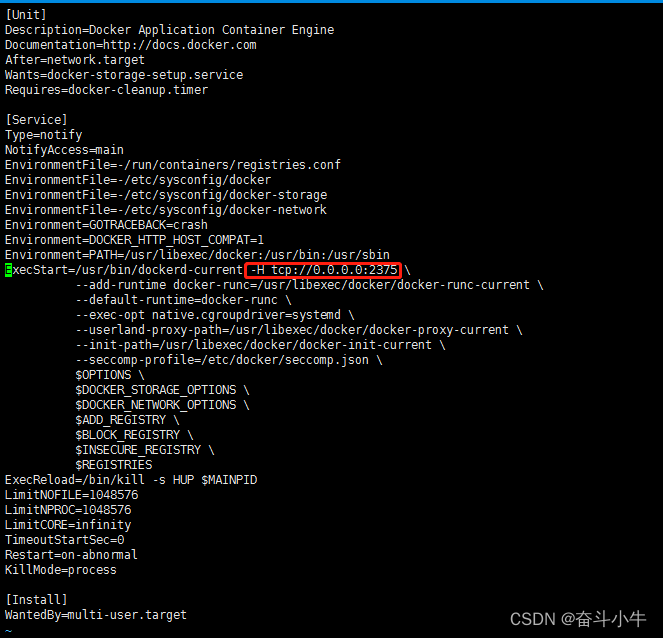
重新加载配置
systemctl daemon-reload
systemctl restart docker
3、idea安装docker插件:
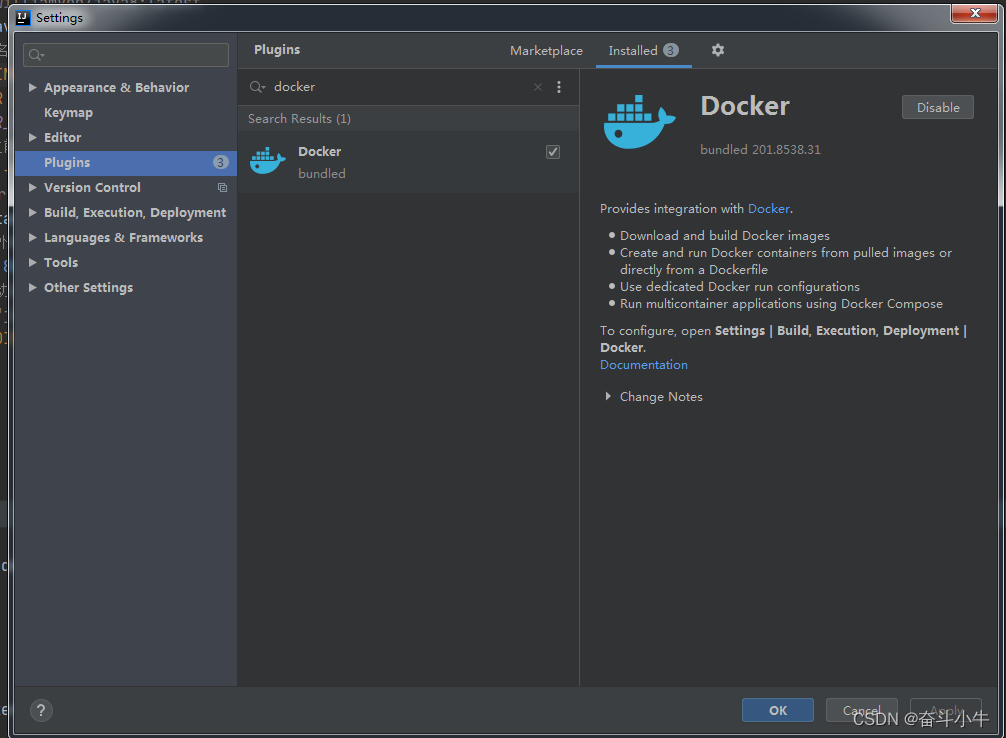
链接docker测试:
docker服务器地址ip+docker端口
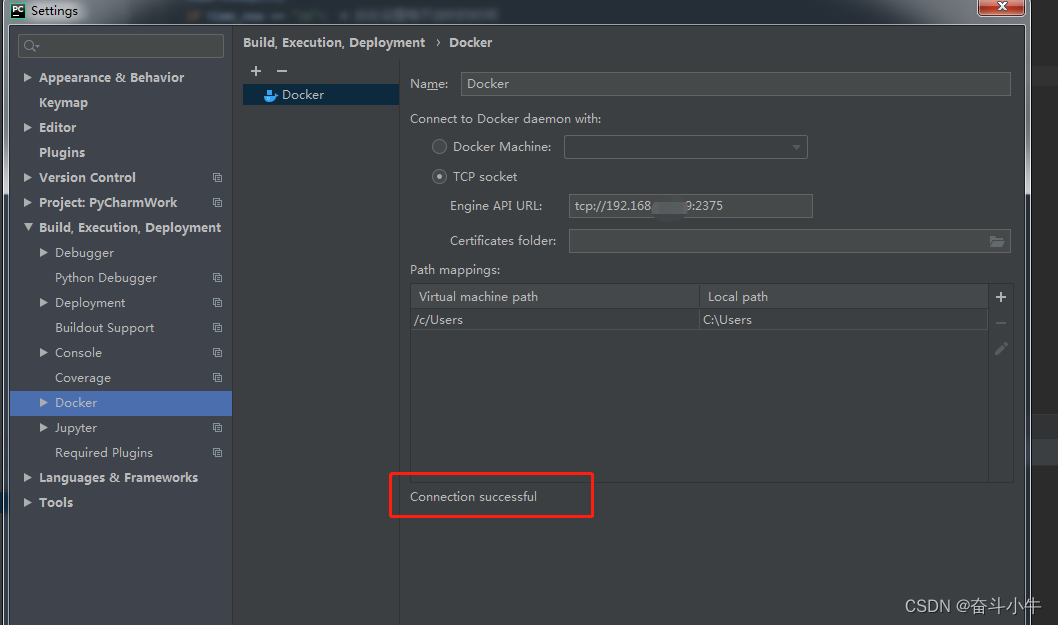
若连接失败:
#查看防火墙状态
systemctl status firewalld
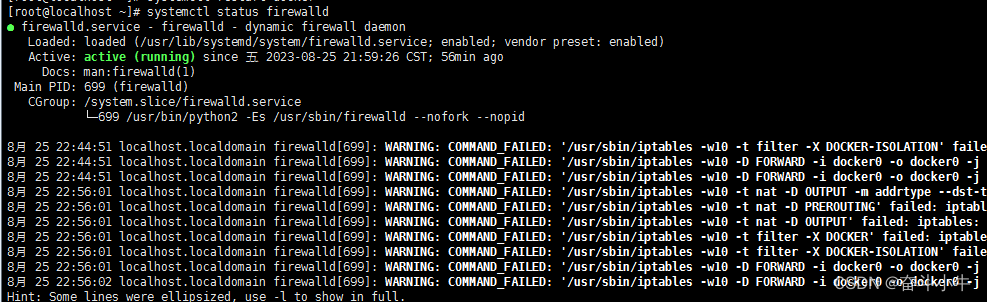
#添加2375端口
firewall-cmd --permanent --zone=public --add-port=2375/tcp
#防火墙重启
firewall-cmd --reload
#查看开放的端口
firewall-cmd --permanent --zone=public --list-ports
#====开启状态下不需要执行==========
#启动防火墙命令
systemctl start firewalld
防火墙配置后idea重新连接测试即可。
4、文件配置
pom.xml引入docker插件:
<!-- docker插件配置 --><plugin><groupId>com.spotify</groupId><artifactId>dockerfile-maven-plugin</artifactId><version>1.4.13</version><executions><execution><id>default</id><goals><goal>build</goal></goals></execution></executions><configuration><!--镜像名字--><repository>${project.artifactId}</repository><tag>${project.version}</tag><buildArgs><JAR_FILE>${project.build.finalName}.jar</JAR_FILE></buildArgs></configuration></plugin>
项目根目录下新建Dockerfile文件:
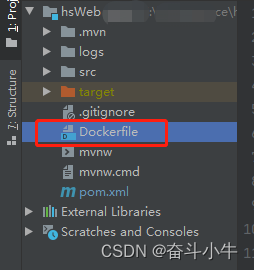
Dockerfile文件内容:
#基础镜像为java8
#FROM williamyeh/java8:latest
FROM java:8
#作者签名
MAINTAINER "zxj"
WORKDIR /app/docker-demo
ARG JAR_FILE
# 删除之前的镜像文件
RUN rm -rf /app/docker-demo/eco*
#拷贝jar包,到容器内的指定位置
ADD ./target/eco-0.0.1-SNAPSHOT.jar /app/docker-demo/eco-0.0.1-SNAPSHOT.jar
#容器对外映射端口,声明运行时容器提供服务端口,这只是一个声明,在运行时并不会因为这个声明应用就会开启这个端口的服务
EXPOSE 8082
#运行启动命令
#CMD ["java", "-jar","-Dfile.encoding=UTF-8","eco-0.0.1-SNAPSHOT.jar","--spring.profiles.active=dev"]
ENTRYPOINT ["java", "-jar","/app/docker-demo/eco-0.0.1-SNAPSHOT.jar"]5、打包镜像并推送至docker服务器
idea执行mvn clean package docker:build

报错:

maven配置docker服务:
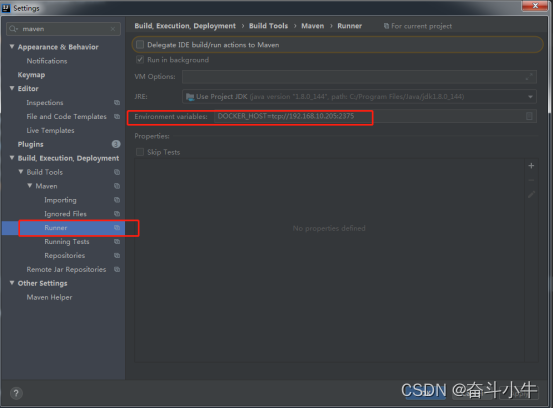
配置环境变量:
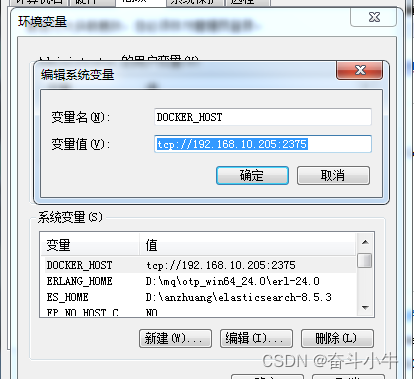
错误提示:
No plugin found for prefix 'docker' in the current project and in the plugin groups
需要在maven的conf/setting.xml中要加入:
<pluginGroups> <pluginGroup>com.spotify</pluginGroup>
</pluginGroups>
依然报错:

最后更换命令成功了:
mvn clean package dockerfile:build
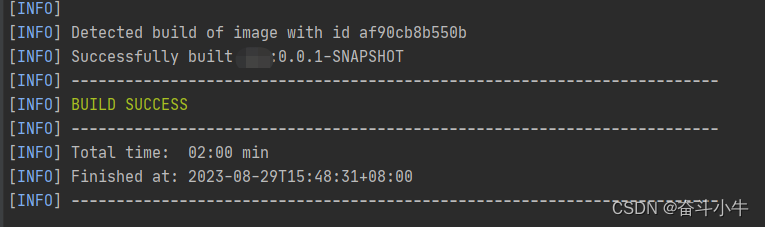
6、运行镜像
查看镜像:
docker images

运行镜像
docker run -d -p 8082:8083 jingxiangname:0.0.1-SNAPSHOT
jingxiangname:0.0.1-SNAPSHOT参数为以下两个参数的值:

docker相关命令:
#启动docker
systemctl start docker#停止docker
systemctl stop docker#重启docker
systemctl restart docker#查看docker状态
systemctl status docker#开机启动
systemctl enable docker#列出所有在运行的容器信息:
docker ps#删除镜像id或名字均可
docker rmi bf756fb1ae65#批量删除关键字镜像,替换命令中的guanjianzi
docker rmi --force `docker images | grep guanjianzi| awk '{print $3}'`
