综合电子商务型企业网站网站品牌词优化怎么做
动态规划(三)
目录
- 动态规划(三)
- 一:线性DP
- 1.数字三角形
- 1.1数字三角形题目
- 1.2代码思路
- 1.3代码实现(正序and倒序)
- 2.最长上升子序列
- 2.1最长上升子序列题目
- 2.2代码思路
- 2.3代码实现
- 3.最长公共子序列
- 3.1最长公共子序列题目
- 3.2代码思路
- 3.3代码实现
- 4.石子合并
- 4.1题目如下
- 4.2代码思路
- 4.3代码实现
- 总结
一:线性DP
1.数字三角形
1.1数字三角形题目
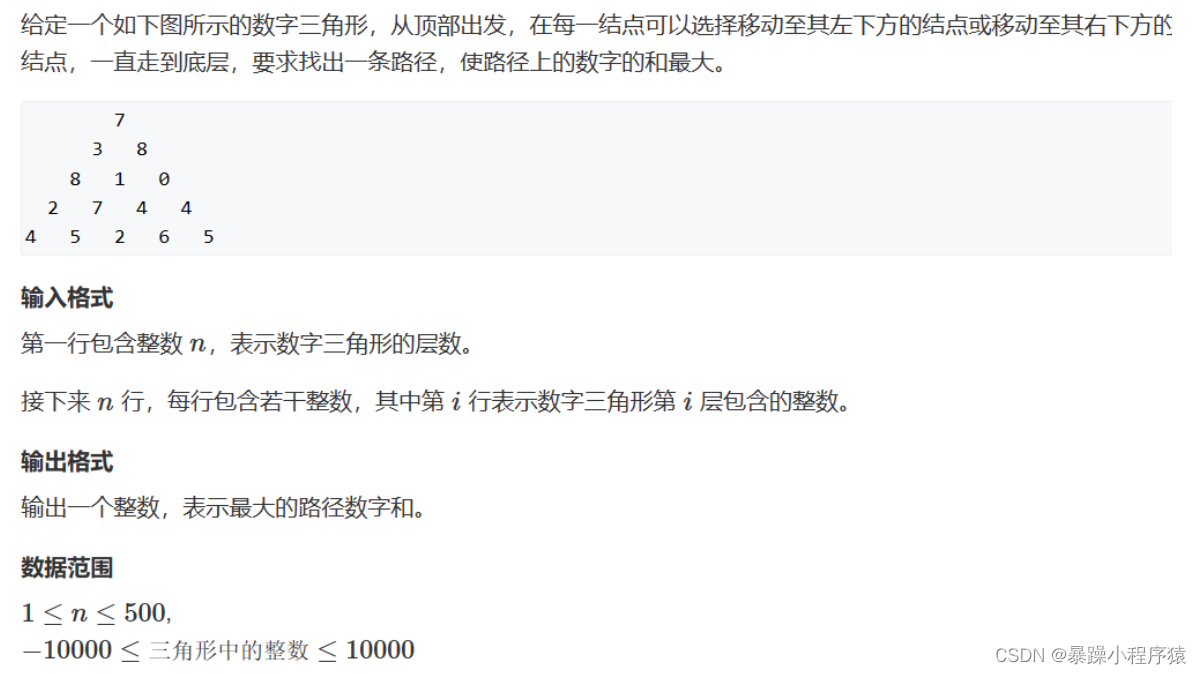
1.2代码思路
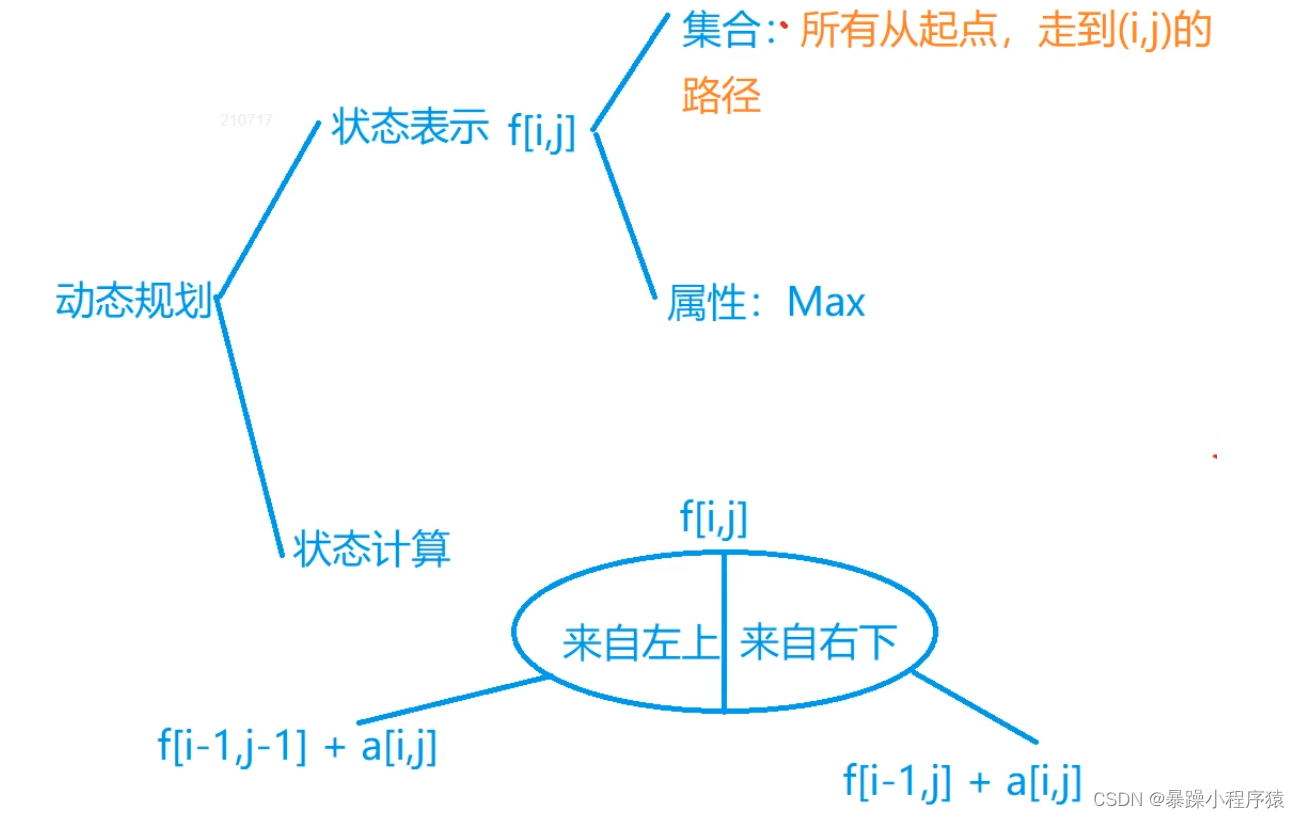
正序思路
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GCHTJR8G-1679754745663)(D:\acwing算法题目思路\acwing图片\image-20230313163539518.png)]](https://img-blog.csdnimg.cn/728b2fe370624df09e03090c5ab66257.png)
倒序思路

1.3代码实现(正序and倒序)
正序版本
#include<bits/stdc++.h>
using namespace std;const int N=510,INF=0x3f3f3f3f;
int f[N][N];
int a[N][N];int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){ for(int j=0;j<=i+1;j++){ //因为有负数,所以应该将两边也设为-INFf[i][j]=-INF;}}f[1][1]=a[1][1];for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);}}int res=-INF;for(int i=1;i<=n;i++) res=max(res,f[n][i]);cout<<res<<endl;
}
倒叙版本(倒序比正序好的地方就在不用考虑边界问题)
#include<bits/stdc++.h>
using namespace std;const int N=510;
int f[N][N];
int n;int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>f[i][j];}}for(int i=n;i>=1;i--){for(int j=i;j>=1;j--){f[i][j]=max(f[i+1][j],f[i+1][j+1])+f[i][j];}}cout<<f[1][1]<<endl;
}
2.最长上升子序列
2.1最长上升子序列题目
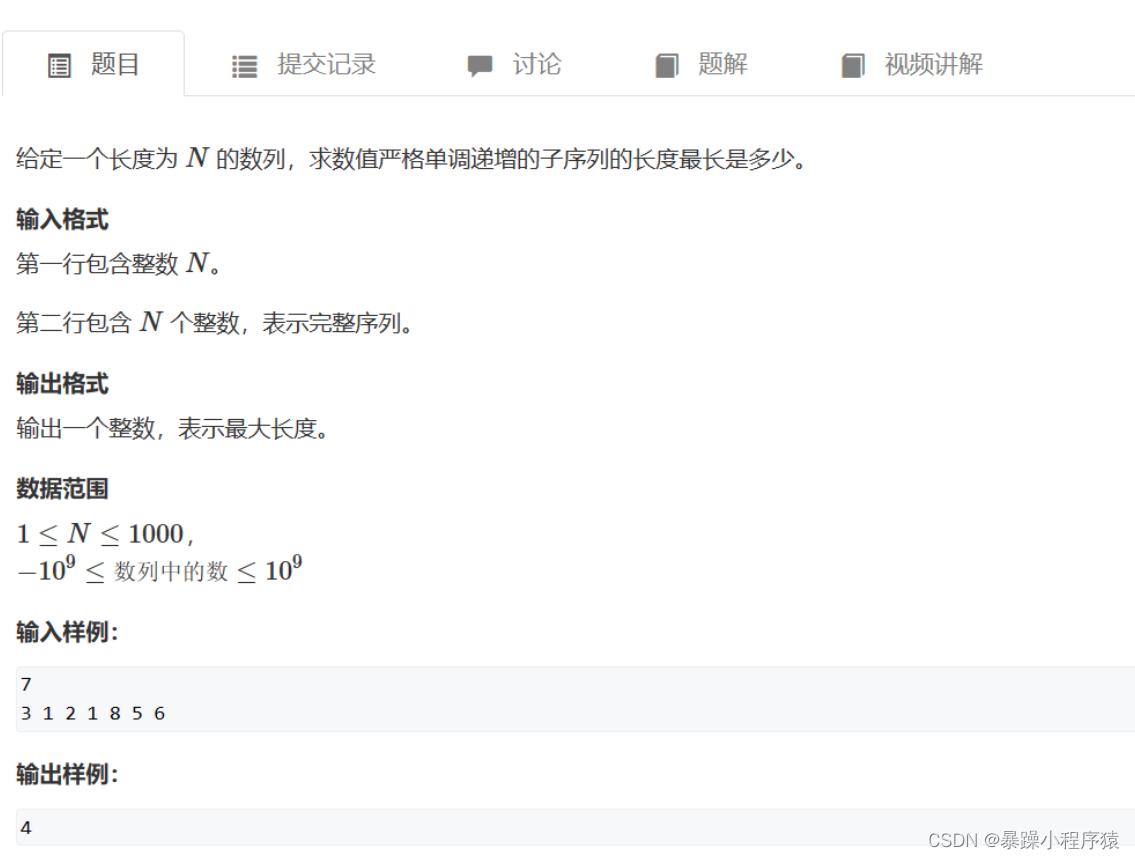
2.2代码思路
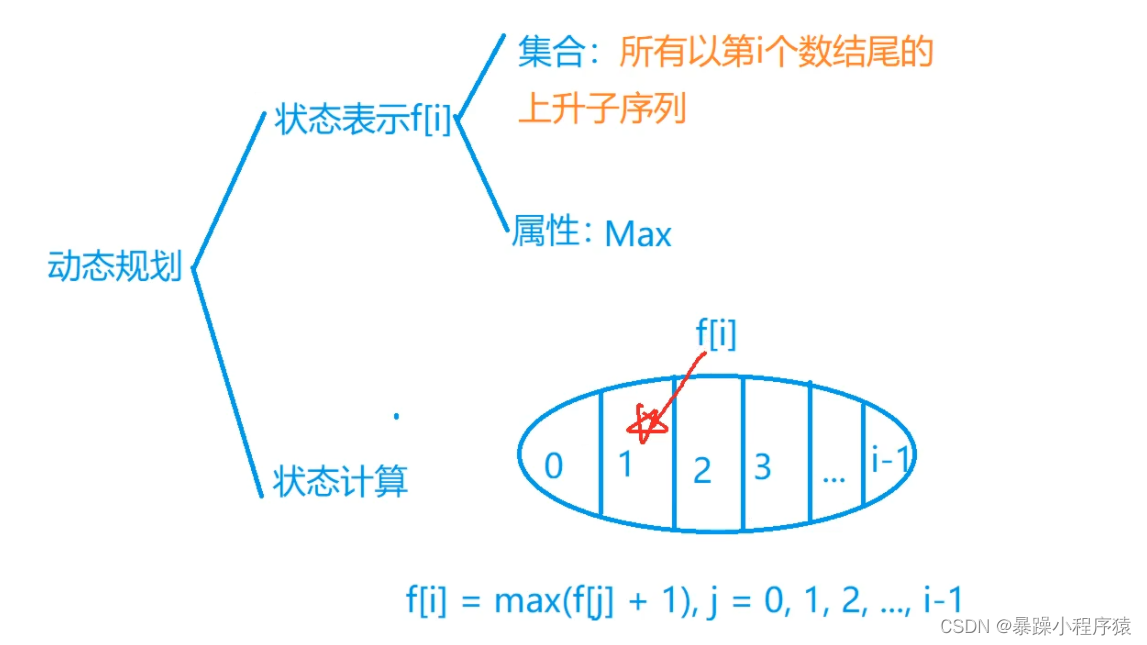

2.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n;
int a[N],f[N];//a[N]我们用来保存长度为n的序列//f[N]表示以指定数字结尾的单调递增的序列的最大长度
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=n;i++){f[i]=1;//只有a[i]一个数符合单调递增for(int j=1;j<i;j++){if(a[j]<a[i]){f[i]=max(f[i],f[j]+1);}}}int res=0;for(int i=1;i<=n;i++){res=max(res,f[i]);}printf("%d\n",res);return 0;
}
3.最长公共子序列
3.1最长公共子序列题目
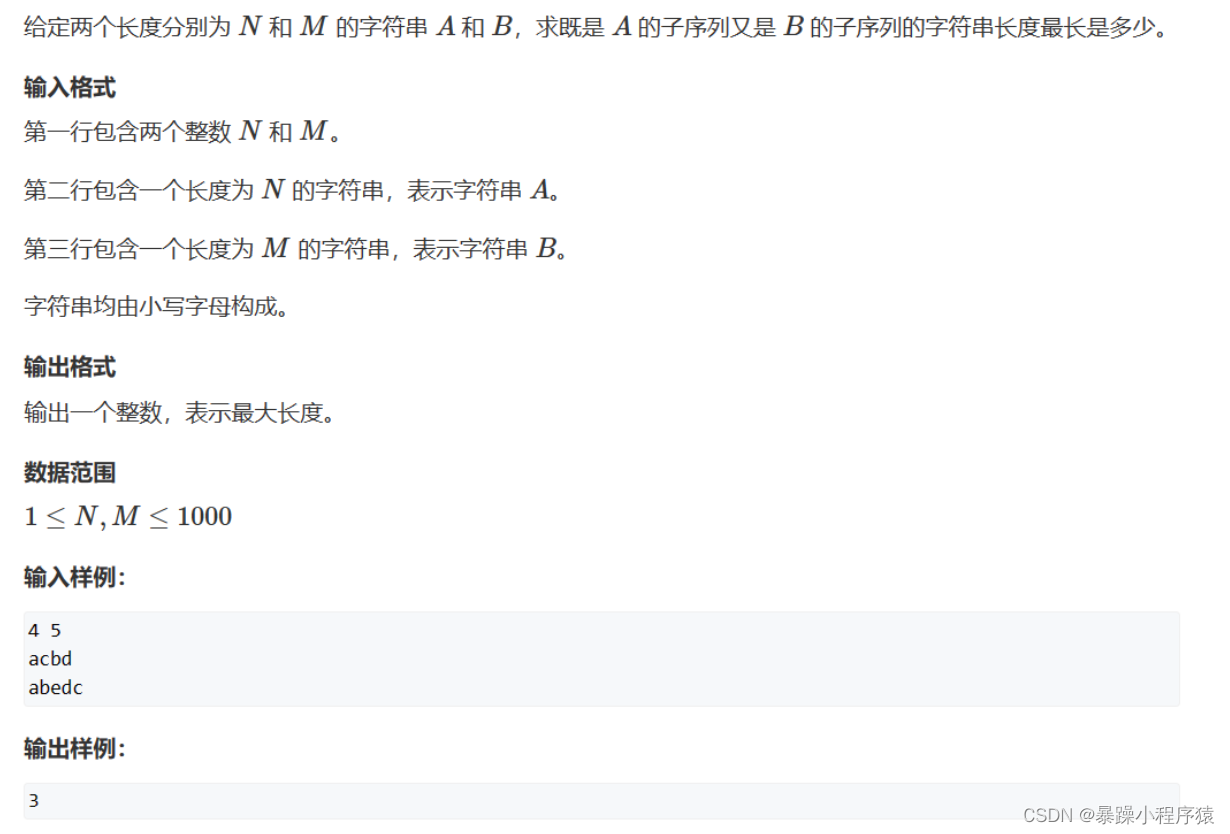
3.2代码思路
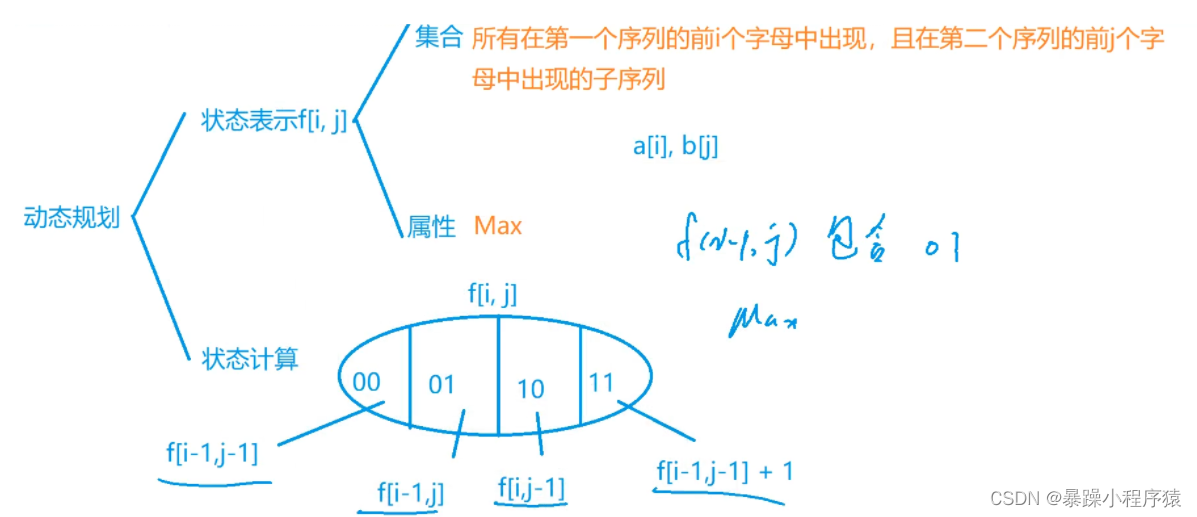
我觉得这题的状态分成两半考虑比较方便,按两个序列末尾的字符是不是相等来区分。
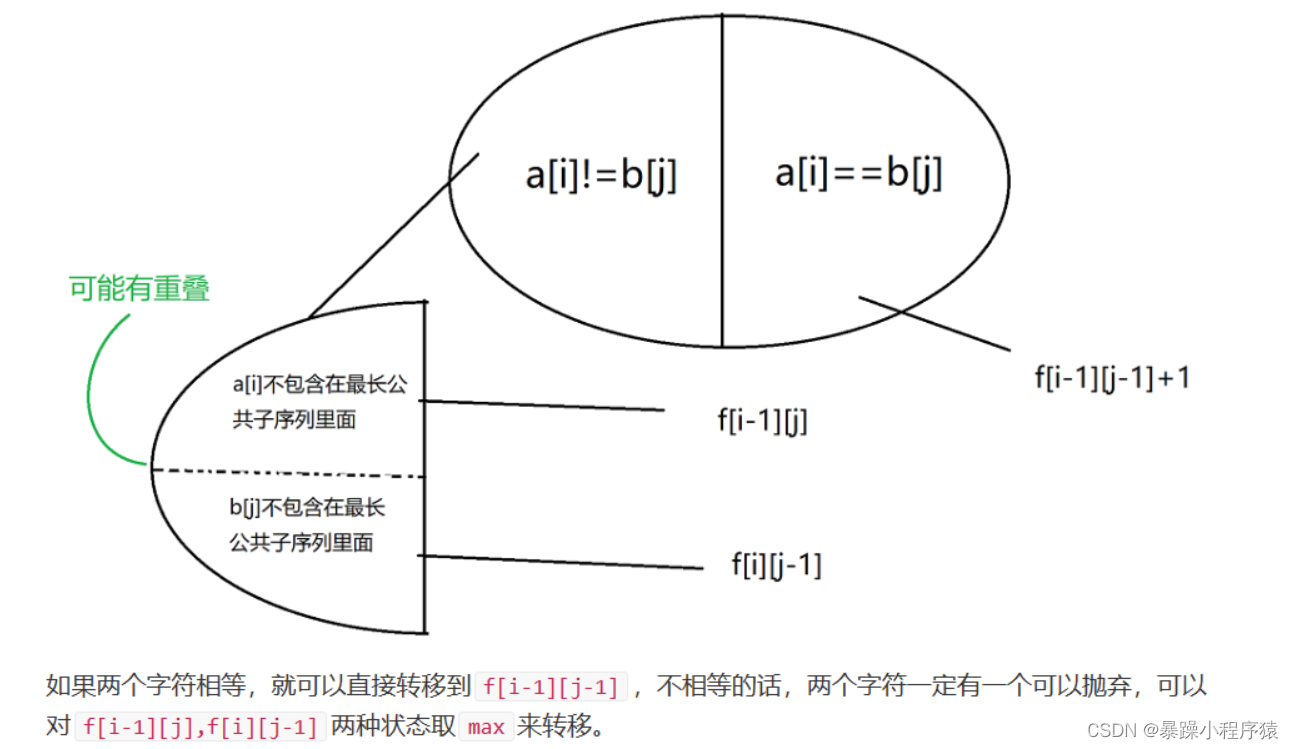
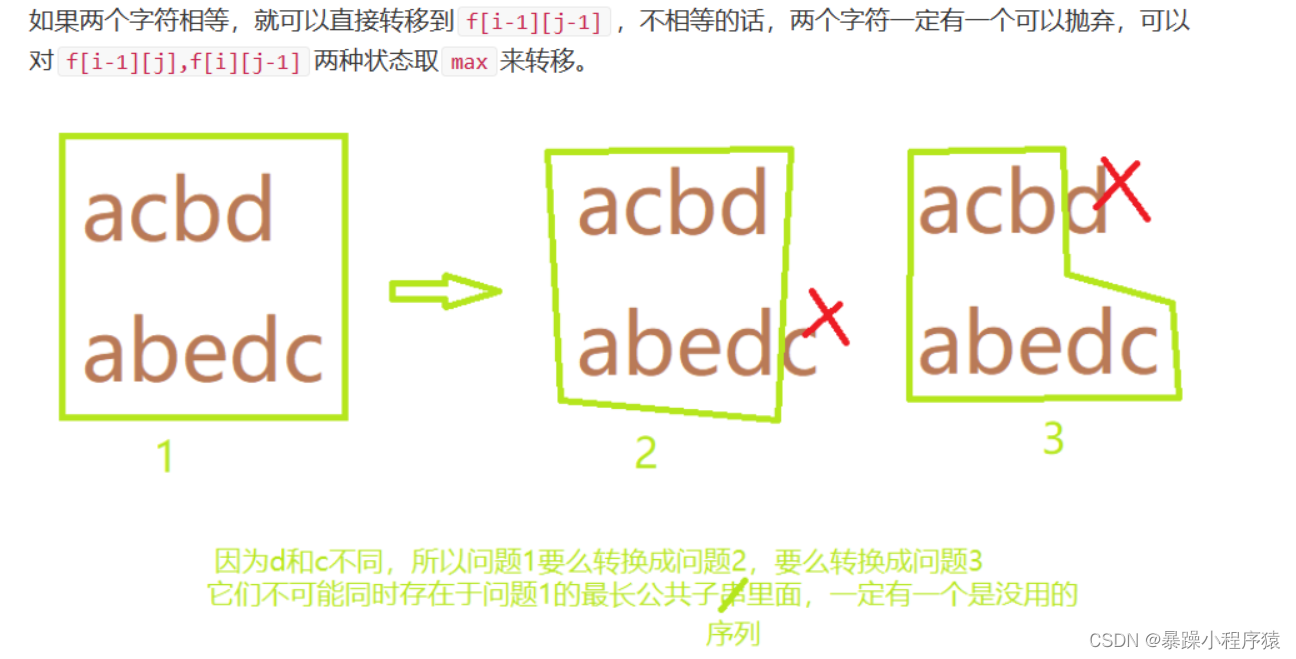
3.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;int n,m;char a[N],b[N];int f[N][N];int main(){scanf("%d%d",&n,&m);scanf("%s%s",a+1,b+1);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1]);if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);}}printf("%d\n",f[n][m]);return 0;}
4.石子合并
4.1题目如下
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lQ6plVYl-1679754745666)(D:\acwing算法题目思路\acwing图片\image-20230313171007224.png)]](https://img-blog.csdnimg.cn/bcbcb23e94834cb9ae8569a1ebcae324.png)
题目分析
假设有4堆石子:1 3 5 2
i=1,k=2,j=4
f[1,2]:将第一堆和第二堆这两堆石子合并成一堆石子
f[3,4]:将第三堆和第四堆这两堆石子合并成一堆石子
所以经过f[1,2]+f[3,4]后我们就成功将1 3 5 2这四堆石子合并成了4 7 这两堆石子
不过别忘了题目要求的是将这四堆石子合并成一堆石子
所以我们还需将4 7 这两堆石子合并成一堆石子
因此还需付出4+7=11的代价;而11=[1,4]的前缀和
总代价:(1+3)+(5+2)+4+7=22
假设有4堆石子:1 3 5 2
i=1,k=2,j=4
f[1,2]:将第一堆和第二堆这两堆石子合并成一堆石子
f[3,4]:将第三堆和第四堆这两堆石子合并成一堆石子
所以经过f[1,2]+f[3,4]后我们就成功将1 3 5 2这四堆石子合并成了4 7 这两堆石子
不过别忘了题目要求的是将这四堆石子合并成一堆石子
所以我们还需将4 7 这两堆石子合并成一堆石子
因此还需付出4+7=11的代价;而11=[1,4]的前缀和
总代价:(1+3)+(5+2)+4+7=22
4.2代码思路
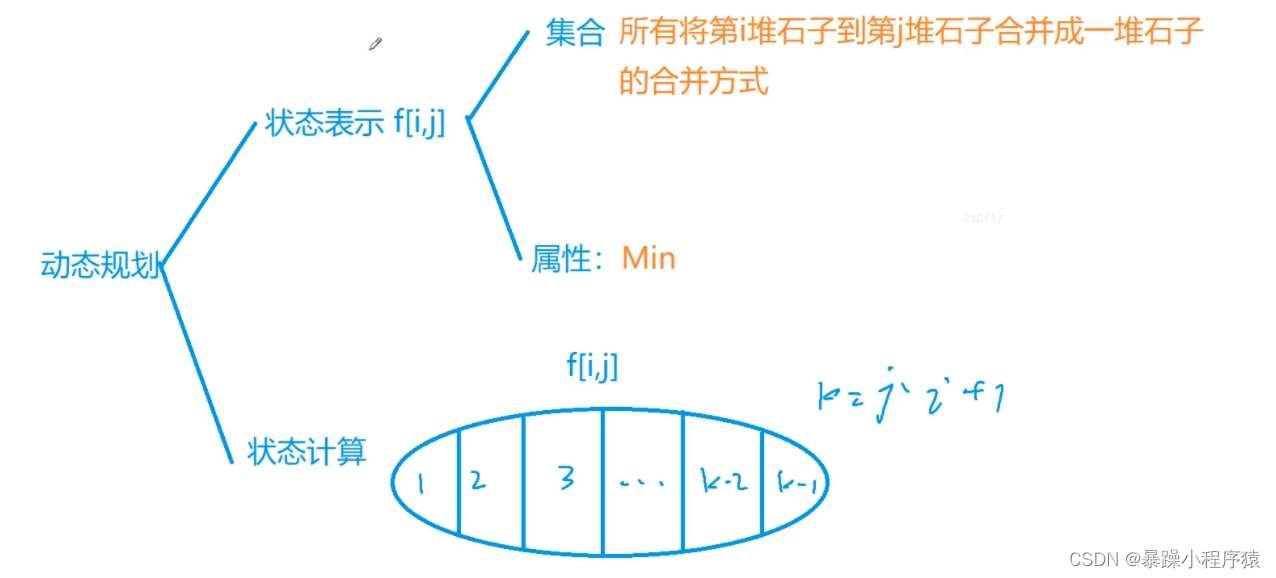
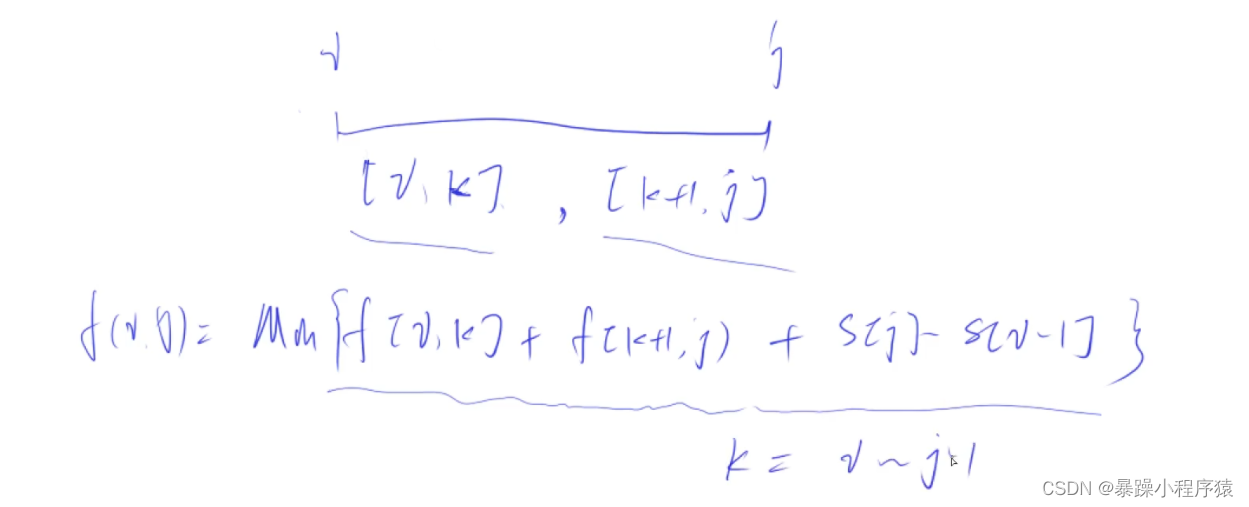
4.3代码实现
#include<iostream>
#include<algorithm>
using namespace std;
const int N=310;
int n;
int s[N];
int f[N][N];int main()
{scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&s[i]);for(int i=1;i<=n;i++) s[i]+=s[i-1];for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int l=i,r=i+len-1;f[i][r]=1e8;for(int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}}}printf("%d\n",f[1][n]);return 0;
}
总结
本篇博客涉及了线性dp和区间dp,还有对应的算法题目讲解帮助理解算法,希望对大家有帮助~
