行业门户网站程序,wordpress 网址全部变成ip,广东省建设注册中心网站,网站优化推广排名抽象工厂模式也是一种创建型设计模式,提供了一个创建一系列相关或相互依赖对象的接口,而无需指定它们具体的类【引用自大话设计模式第15章】基本结构 抽象工厂模式包含多个抽象产品接口,多个具体产品类,一个抽象工厂接口和多个具体…- 抽象工厂模式也是一种创建型设计模式,提供了一个创建一系列相关或相互依赖对象的接口,而无需指定它们具体的类【引用自大话设计模式第15章】
- 基本结构
- 抽象工厂模式包含多个抽象产品接口,多个具体产品类,一个抽象工厂接口和多个具体工厂,每个具体工厂负责创建一组相关的产品。
通俗解释: - 抽象产品接口AbstractProduct: 定义产品的接口,可以定义多个抽象产品接口,比如说沙发、椅子、茶几都是抽象产品。
- 具体产品类ConcreteProduct: 实现抽象产品接口,产品的具体实现,古典风格和沙发和现代风格的沙发都是具体产品。
- 抽象工厂接口AbstractFactory: 声明一组用于创建产品的方法,每个方法对应一个产品。
- 具体工厂类ConcreteFactory: 实现抽象工厂接口,负责创建一组具体产品的对象,在本例中,生产古典风格的工厂和生产现代风格的工厂都是具体实例。
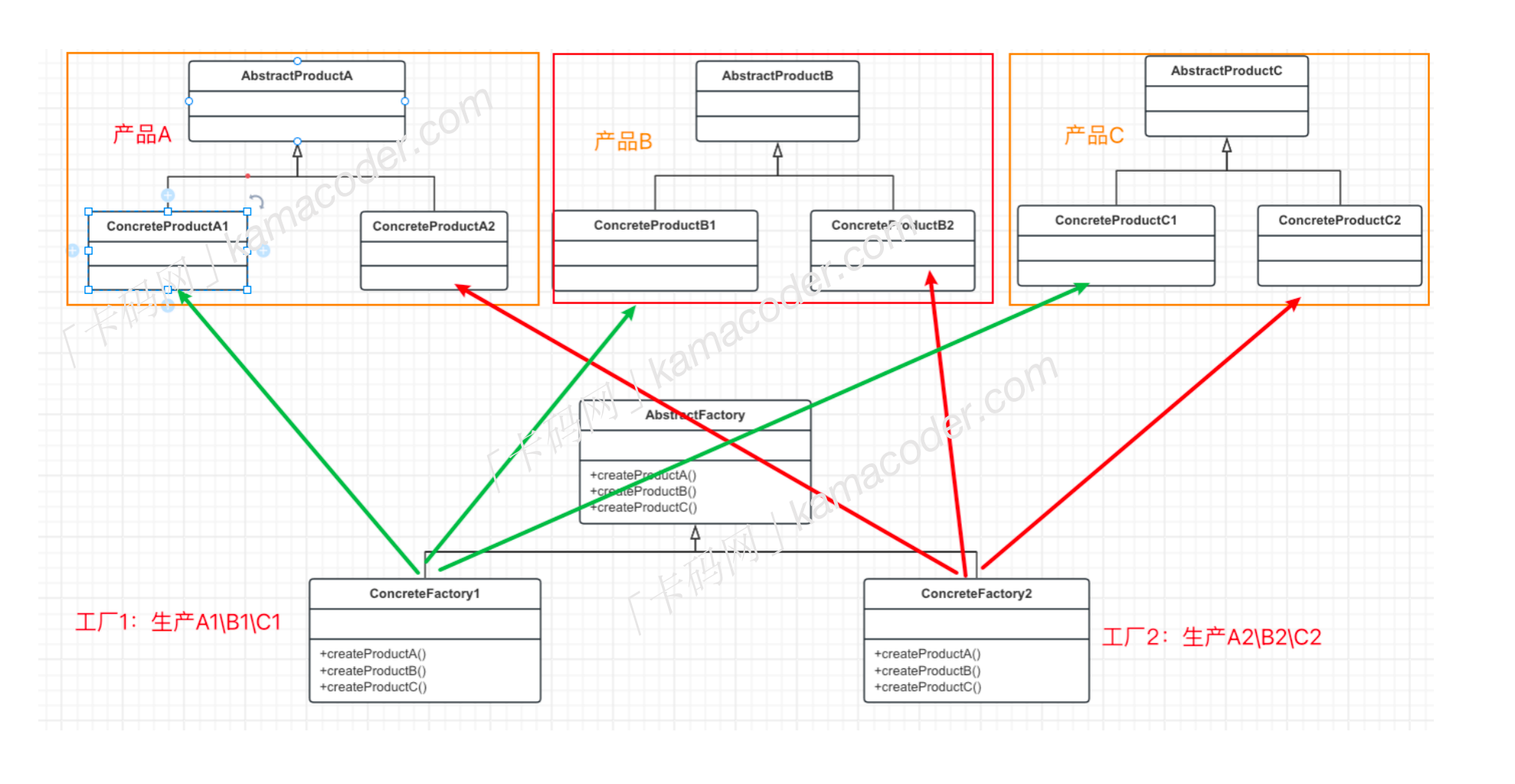
- 在图示中:AbstractProductA/B/C 就是抽象产品,ConcreteProductA2/A2/B1/B2/C1/C2就是抽象产品的实现,AbstractFactory定义了抽象工厂接口,接口里的方法用于创建具体的产品,而ConcreteFactory就是具体工厂类,可以创建一组相关的产品。
- 基本实现
想要实现抽象工厂模式,需要遵循以下步骤: - 定义抽象产品接口(可以有多个),接口中声明产品的公共方法。
- 实现具体工厂类,分别实现抽象工厂接口中的方法,每个方法负责创建一组相关的产品。
- 在客户端中使用抽象工厂和抽象产品,而不直接使用具体产品的类名。
- 应用场景
- 抽象工厂模式能够保证一系列相关的产品一起使用,并且在不修改客户端代码的情况下,可以方便地替换整个产品系列。但是当需要增加新的产品类时,除了要增加新的具体产品类,还需要修改抽象工厂接口及其所有的具体工厂类,扩展性相对较差。因此抽象工厂模式特别适用于一系列相关或相互依赖的产品被一起创建的情况,典型的应用场景是使用抽象工厂模式来创建与不同数据库的连接对象。

