Hdi做指数网站wordpress 实现注册
目录:导读
- 前言
- 一、Python编程入门到精通
- 二、接口自动化项目实战
- 三、Web自动化项目实战
- 四、App自动化项目实战
- 五、一线大厂简历
- 六、测试开发DevOps体系
- 七、常用自动化测试工具
- 八、JMeter性能测试
- 九、总结(尾部小惊喜)
前言
1、接口调不通,如何去排查?
1)接口没有任何响应
很多时候在做接口测试时,会发现接口没有任何返回,比如浏览器一直在转圈,或者返回一个空白页面。用接口测试工具时,工具报错,提示“no response”。
排查思路:
先检查接口ip是否正确,可以通过在本机ping 接口的ip,检查网络是否通畅
再检查接口的端口号是否正确,可以通过在本机telnet接口的ip和端口号,检查端口是否能连通
检查项目是否启动或者部署成功,可以找研发确认,或者自己登录到服务器上,通过ps命令检查项目的进程是否存在,然后用tail命令查看部署日志
检查服务器防火墙是否关闭,如果因为安全或者权限问题不能关闭,需要找运维进行策略配置,开放对应的ip和端口号
检查你的客户端(浏览器/测试工具),是否设置了网络代理,网络代理可能会造成请求失败
检查操作系统的host文件,是否绑定了一个错误的ip映射
2)接口有响应但是返回了错误的状态码
有些时候接口会返回一些错误的HTTP状态码,需要根据不同的状态码来确定具体的原因。
排查思路
400:客户端请求错误,比如请求参数格式错误(如json字符串不合法)
401:未授权,比如在请求header里,缺乏必要的信息头(如token、auth等字段)
403:禁止,常见的原因是用户的账号没有对应的url权限,还有就是项目所用的中间件,不允许远程访问(比如Apache)
404:资源未找到,导致这种情况的原因很多,比如:
a> url写错了
b> url后有空格
c> 项目没有启动成功
d> 请求协议不对,如http/https
405:方法不允许,常见的原因是请求方式不正确,比如GET类型接口,使用POST方式去请求
415:不支持的媒体类型,常见原因是请求数据的类型和服务端支持的类型不匹配,比如json接口,需要添加一个信息头Content-type:application/json
500:服务器内部错误,出现这种情况,说明服务端内部报错了,需要登录到服务器上,检查错误日志,根据具体的提示信息再进行排查
502/503/504(Bad Gateway/错误的网关、Service Unavailable/服务无法获得、Gateway Timeout/网关超时)
a>如果单次调用接口就报该错误,说明是后端服务器配置有问题,或者服务不可用,挂掉了
b>如果并发压测时出现此错误,说明是后端压力太大,出现异常,此问题一般是后端出现了响应时间过长或者无响应造成的
2、接口测试常遇面试题
1)怎么理解同步通信?
同步通信指的是客户端发送请求给服务端,服务端必须得回应客户端的请求,也就是说有请求就必须有回应,所以也正因为这个问题同步通信就会出现超时或者堵塞的问题
2)怎么理解异步通信?
异步通信指的是客户端和服务端之间根本不知道对方的存在,他们中间通过消息队列来进行整个通信的,也就说客户端把消息发送给消息队列,服务端从消息队列里面拿取到对应的消息,服务端处理完成后会把这个消息发送给消息队列,然后客户端从消息队列获取这个数据,所以他们根据不知道对方的存在
3)怎么理解cookie,session,token?
HTTP协议是一个无状态协议,所以导致cookie技术的整个发展,cookie是记录用户操作行为的一个状态,但是它存储在客户端,它是不安全的,所以呢我们有整个session,session它是这个存储在服务端的,我们把他成为一个令牌
请按步骤的方式描述session的请求流程
客户端提交账户和密码登陆成功
服务端会生成一个sessionid, 并且存储在服务端,服务端通过set-cookie把生成的sessionid响应给客户端
客户端再次请求服务端,会在请求头里带上sessionid 发送给服务端
服务端接收到sessionid和服务端本地存储的sessionid进行比较,如果相符允许访问个人主页,如果不相符 ,则返回登陆页面
4)如果发送请求,协议状态码返回500的错误,怎么解决?
这个是服务端内部错误,这个是需要找程序员的
5)如何理解协议状态码和业务状态码?
协议状态码是标准的
业务状态码是程序员自己定义的,想怎么定义就怎么定义,很随机很自由。
6)按步骤的方式描述token的请求流程?
按步骤的方式描述cookie的请求流程
以登陆为案例来说明cookie的流程
客户端输入账户和密码登陆成功
服务端生成cookie的信息,通过响应头中的set-cookie把生成的cookie返回给客户端。
客户端在下次请求的时候,通过请求头中的cookie把返回的cookie带上发送给服务端,服务端内部进行验证
7)在get请求里面。如果有请求参数,使用的参数是那个的?
我们在postman中我们通过params,路径参数,如果在jmeter中我们直接添加到路径的请求地址里面
8)在postman里面在哪里填写请求参数?
如果是get请求,那么它的路径参数就是在params,如果是POST请求他的数据格式是表单那么我们是在Body里面勾选x-www,如果是json的格式那么我们raw里面勾线json填写json的数据格式,如果是XML的格式那么我们就勾选XML在里面填写XML的数据格式
9)详细描述下API自动化测试的流程?
首先我们先梳理产品过程当中哪些模块可以做自动化测试,梳理完成后,我们和相关的主管领导去对一下,对完之后我们通过jmeter工具或者postman工具,我们把复盘之后我们就上相关的领导进行评审,评审看我们的断言对不对,看你的结构对不对
10)详细描述下你使用ant是怎么做API的测试的
JMeter整合Ant工具来生成测试报告步骤:
搭建ant的环境,(把 ant 的bin路径加在path里面)验证方式:ant -v
在jmerer的extras目录下找到ant-jmeter-1.1.1.jar,把它copy到ant的apache-ant-1.10.0\lib下
编写build.xml文件
定义了执行那个测试脚本
实现自动发送邮件
自动生成测试报告
打开jmeter的bin目录下的jmeter.properties文件,做如下修改:
把jmeter.save.saveservice.output_format=csv
修改为jmeter.save.saveservice.output_format=xml
activation.jar,commons-email-1.2.jar,mail.jar,这三个文件放在ant的lib目录下
完善build.xml文件后,在控制台进入到build.xml文件
输入ant即可
| 下面是我整理的2023年最全的软件测试工程师学习知识架构体系图 |
一、Python编程入门到精通

二、接口自动化项目实战
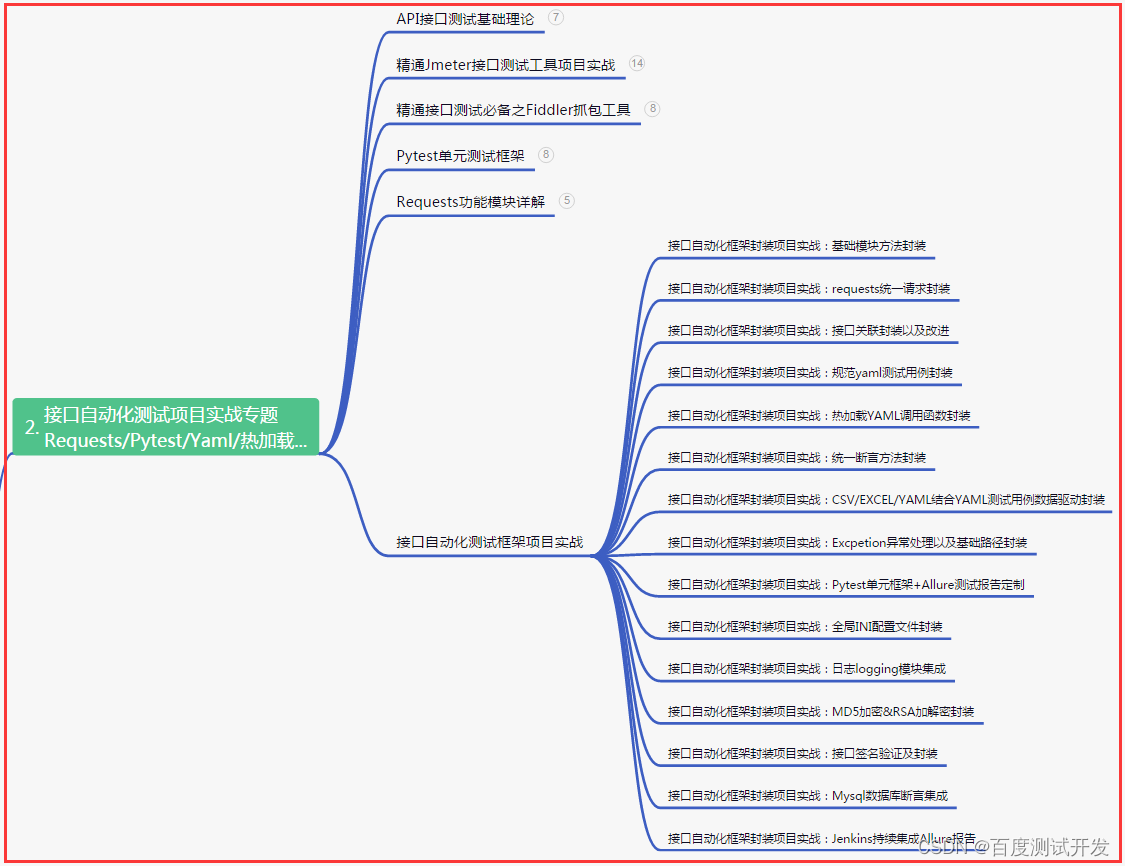
三、Web自动化项目实战
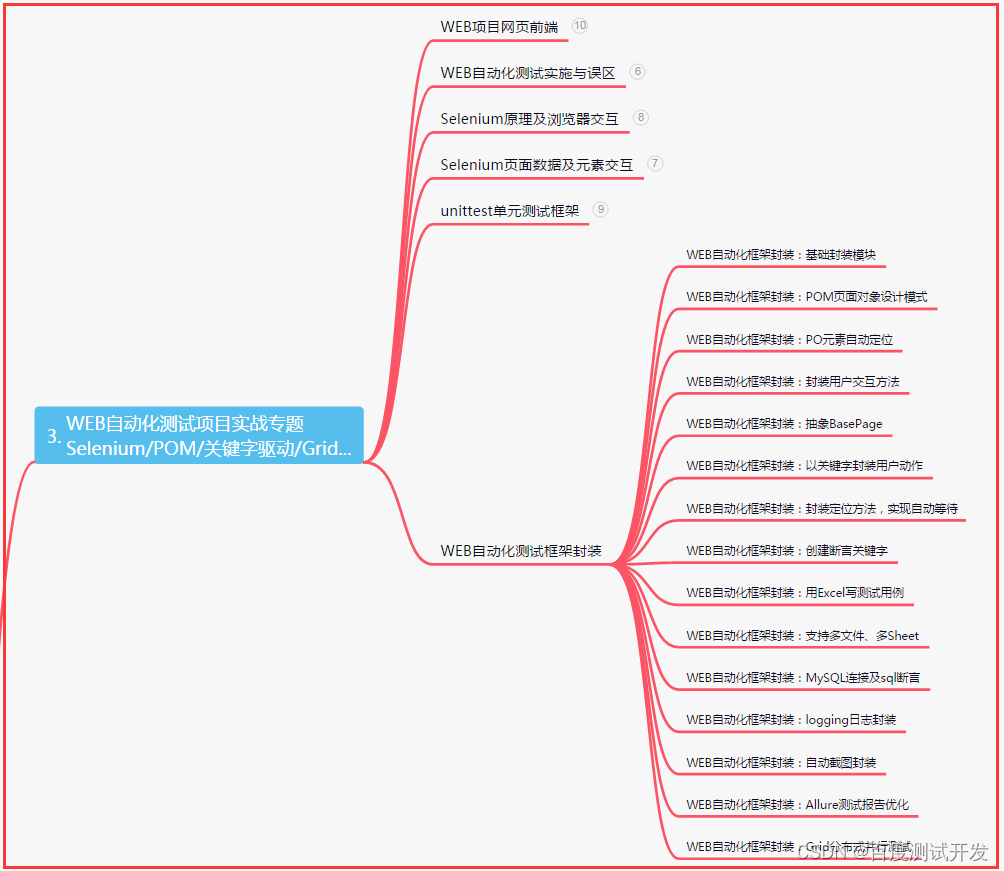
四、App自动化项目实战
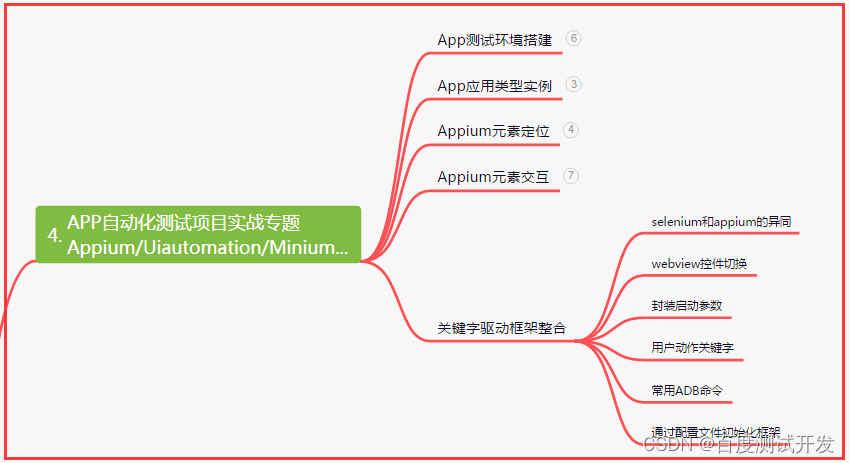
五、一线大厂简历
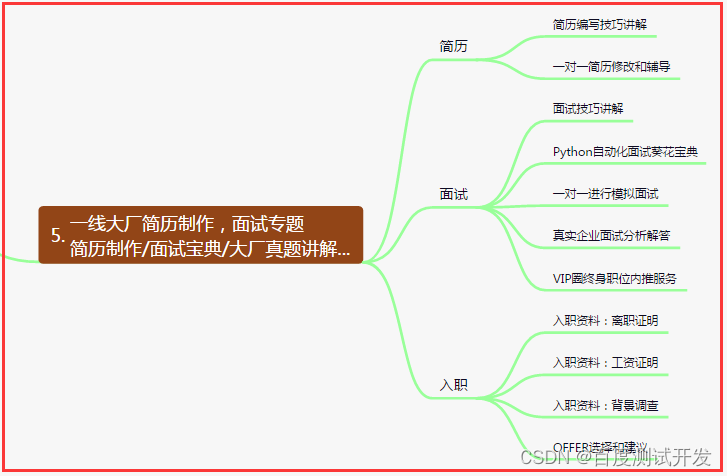
六、测试开发DevOps体系
七、常用自动化测试工具

八、JMeter性能测试
九、总结(尾部小惊喜)
每一次努力都是自己的投资,每一份付出都将成就更加辉煌的未来。坚定前行,勇往直前,因为只有不断超越自己,才能成就非凡。
生命因奋斗而绽放,每一份汗水都是未来的灿烂;坚韧不拔,才能走出属于自己的辉煌之路。别停下脚步,因为你可以更强大。
在每一个黎明之前,总有黑夜的挣扎;在每一次坠落之后,必有勇气的奋起。不放弃,不言败,让梦想的火焰照亮前行的路途。
