六安网站推广免费制作地图app
1.HTTP简介
HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)的缩写,是用于从万维网(WWW:World Wide Web )服务器传输超文本到本地浏览器的传送协议。
HTTP是一个基于TCP/IP通信协议来传递数据(HTML 文件, 图片文件, 查询结果等)。
HTTP是一个属于应用层的面向对象的协议,由于其简捷、快速的方式,适用于分布式超媒体信息系统。它于1990年提出,经过几年的使用与发展,得到不断地完善和扩展。目前在WWW中使用的是HTTP/1.0的第六版,HTTP/1.1的规范化工作正在进行之中,而且HTTP-NG(Next Generation of HTTP)的建议已经提出。
HTTP协议工作于客户端-服务端架构为上。浏览器作为HTTP客户端通过URL向HTTP服务端即WEB服务器发送所有请求。Web服务器根据接收到的请求后,向客户端发送响应信息。

http请求-响应模型.jpg
2.主要特点
1、简单快速:客户向服务器请求服务时,只需传送请求方法和路径。请求方法常用的有GET、HEAD、POST。每种方法规定了客户与服务器联系的类型不同。由于HTTP协议简单,使得HTTP服务器的程序规模小,因而通信速度很快。
2、灵活:HTTP允许传输任意类型的数据对象。正在传输的类型由Content-Type加以标记。
3.无连接:无连接的含义是限制每次连接只处理一个请求。服务器处理完客户的请求,并收到客户的应答后,即断开连接。采用这种方式可以节省传输时间。
4.无状态:HTTP协议是无状态协议。无状态是指协议对于事务处理没有记忆能力。缺少状态意味着如果后续处理需要前面的信息,则它必须重传,这样可能导致每次连接传送的数据量增大。另一方面,在服务器不需要先前信息时它的应答就较快。
5、支持B/S及C/S模式。
3.HTTP之URL
HTTP使用统一资源标识符(Uniform Resource Identifiers, URI)来传输数据和建立连接。URL是一种特殊类型的URI,包含了用于查找某个资源的足够的信息
URL,全称是UniformResourceLocator, 中文叫统一资源定位符,是互联网上用来标识某一处资源的地址。以下面这个URL为例,介绍下普通URL的各部分组成:
http://www.aspxfans.com:8080/news/index.asp?boardID=5&ID=24618&page=1#name
从上面的URL可以看出,一个完整的URL包括以下几部分:
1.协议部分:该URL的协议部分为“http:”,这代表网页使用的是HTTP协议。在Internet中可以使用多种协议,如HTTP,FTP等等本例中使用的是HTTP协议。在"HTTP"后面的“//”为分隔符
2.域名部分:该URL的域名部分为“www.aspxfans.com”。一个URL中,也可以使用IP地址作为域名使用
3.端口部分:跟在域名后面的是端口,域名和端口之间使用“:”作为分隔符。端口不是一个URL必须的部分,如果省略端口部分,将采用默认端口
4.虚拟目录部分:从域名后的第一个“/”开始到最后一个“/”为止,是虚拟目录部分。虚拟目录也不是一个URL必须的部分。本例中的虚拟目录是“/news/”
5.文件名部分:从域名后的最后一个“/”开始到“?”为止,是文件名部分,如果没有“?”,则是从域名后的最后一个“/”开始到“#”为止,是文件部分,如果没有“?”和“#”,那么从域名后的最后一个“/”开始到结束,都是文件名部分。本例中的文件名是“index.asp”。文件名部分也不是一个URL必须的部分,如果省略该部分,则使用默认的文件名
6.锚部分:从“#”开始到最后,都是锚部分。本例中的锚部分是“name”。锚部分也不是一个URL必须的部分
7.参数部分:从“?”开始到“#”为止之间的部分为参数部分,又称搜索部分、查询部分。本例中的参数部分为“boardID=5&ID=24618&page=1”。参数可以允许有多个参数,参数与参数之间用“&”作为分隔符。
(原文:详解URL的组成_一个链接的组成-CSDN博客 )
4.URI和URL的区别
URI,是uniform resource identifier,统一资源标识符,用来唯一的标识一个资源。
Web上可用的每种资源如HTML文档、图像、视频片段、程序等都是一个来URI来定位的
URI一般由三部组成:
①访问资源的命名机制
②存放资源的主机名
③资源自身的名称,由路径表示,着重强调于资源。
URL是uniform resource locator,统一资源定位器,它是一种具体的URI,即URL可以用来标识一个资源,而且还指明了如何locate这个资源。
URL是Internet上用来描述信息资源的字符串,主要用在各种WWW客户程序和服务器程序上,特别是著名的Mosaic。
采用URL可以用一种统一的格式来描述各种信息资源,包括文件、服务器的地址和目录等。URL一般由三部组成:
①协议(或称为服务方式)
②存有该资源的主机IP地址(有时也包括端口号)
③主机资源的具体地址。如目录和文件名等
URN,uniform resource name,统一资源命名,是通过名字来标识资源,比如mailto:java-net@java.sun.com。
URI是以一种抽象的,高层次概念定义统一资源标识,而URL和URN则是具体的资源标识的方式。URL和URN都是一种URI。笼统地说,每个 URL 都是 URI,但不一定每个 URI 都是 URL。这是因为 URI 还包括一个子类,即统一资源名称 (URN),它命名资源但不指定如何定位资源。上面的 mailto、news 和 isbn URI 都是 URN 的示例。
在Java的URI中,一个URI实例可以代表绝对的,也可以是相对的,只要它符合URI的语法规则。而URL类则不仅符合语义,还包含了定位该资源的信息,因此它不能是相对的。
在Java类库中,URI类不包含任何访问资源的方法,它唯一的作用就是解析。
相反的是,URL类可以打开一个到达资源的流。
5.HTTP之请求消息Request
客户端发送一个HTTP请求到服务器的请求消息包括以下格式:
请求行(request line)、请求头部(header)、空行和请求数据四个部分组成。

Http请求消息结构.png
- 请求行以一个方法符号开头,以空格分开,后面跟着请求的URI和协议的版本。
Get请求例子,使用Charles抓取的request:
GET /562f25980001b1b106000338.jpg HTTP/1.1
Host img.mukewang.com
User-Agent Mozilla/5.0 (Windows NT 10.0; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/51.0.2704.106 Safari/537.36
Accept image/webp,image/*,*/*;q=0.8
Referer http://www.imooc.com/
Accept-Encoding gzip, deflate, sdch
Accept-Language zh-CN,zh;q=0.8第一部分:请求行,用来说明请求类型,要访问的资源以及所使用的HTTP版本.
GET说明请求类型为GET,[/562f25980001b1b106000338.jpg]为要访问的资源,该行的最后一部分说明使用的是HTTP1.1版本。
第二部分:请求头部,紧接着请求行(即第一行)之后的部分,用来说明服务器要使用的附加信息
从第二行起为请求头部,HOST将指出请求的目的地.User-Agent,服务器端和客户端脚本都能访问它,它是浏览器类型检测逻辑的重要基础.该信息由你的浏览器来定义,并且在每个请求中自动发送等等
第三部分:空行,请求头部后面的空行是必须的
即使第四部分的请求数据为空,也必须有空行。
第四部分:请求数据也叫主体,可以添加任意的其他数据。
这个例子的请求数据为空。
POST请求例子,使用Charles抓取的request:
POST / HTTP1.1
Host:www.wrox.com
User-Agent:Mozilla/4.0 (compatible; MSIE 6.0; Windows NT 5.1; SV1; .NET CLR 2.0.50727; .NET CLR 3.0.04506.648; .NET CLR 3.5.21022)
Content-Type:application/x-www-form-urlencoded
Content-Length:40
Connection: Keep-Alivename=Professional%20Ajax&publisher=Wiley第一部分:请求行,第一行明了是post请求,以及http1.1版本。
第二部分:请求头部,第二行至第六行。
第三部分:空行,第七行的空行。
第四部分:请求数据,第八行。
6.HTTP之响应消息Response
一般情况下,服务器接收并处理客户端发过来的请求后会返回一个HTTP的响应消息。
HTTP响应也由四个部分组成,分别是:状态行、消息报头、空行和响应正文。
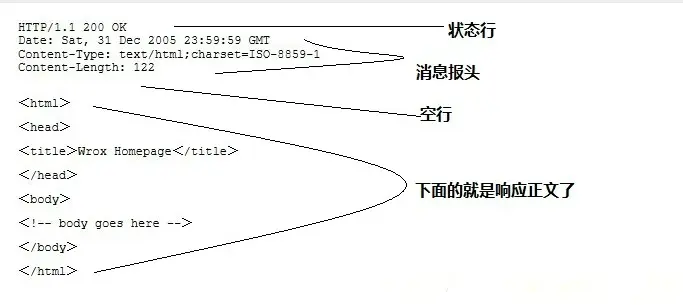
http响应消息格式.jpg
例子
HTTP/1.1 200 OK
Date: Fri, 22 May 2009 06:07:21 GMT
Content-Type: text/html; charset=UTF-8<html><head></head><body><!--body goes here--></body>
</html>第一部分:状态行,由HTTP协议版本号, 状态码, 状态消息 三部分组成。
第一行为状态行,(HTTP/1.1)表明HTTP版本为1.1版本,状态码为200,状态消息为(ok)
第二部分:消息报头,用来说明客户端要使用的一些附加信息
第二行和第三行为消息报头,
Date:生成响应的日期和时间;Content-Type:指定了MIME类型的HTML(text/html),编码类型是UTF-8
第三部分:空行,消息报头后面的空行是必须的
第四部分:响应正文,服务器返回给客户端的文本信息。
空行后面的html部分为响应正文。
7.HTTP之状态码
状态代码有三位数字组成,第一个数字定义了响应的类别,共分五种类别:
1xx:指示信息--表示请求已接收,继续处理
2xx:成功--表示请求已被成功接收、理解、接受
3xx:重定向--要完成请求必须进行更进一步的操作
4xx:客户端错误--请求有语法错误或请求无法实现
5xx:服务器端错误--服务器未能实现合法的请求
常见状态码:
200 OK //客户端请求成功
400 Bad Request //客户端请求有语法错误,不能被服务器所理解
401 Unauthorized //请求未经授权,这个状态代码必须和WWW-Authenticate报头域一起使用
403 Forbidden //服务器收到请求,但是拒绝提供服务
404 Not Found //请求资源不存在,eg:输入了错误的URL
500 Internal Server Error //服务器发生不可预期的错误
503 Server Unavailable //服务器当前不能处理客户端的请求,一段时间后可能恢复正常更多状态码HTTP 状态码 | 菜鸟教程
8.HTTP请求方法
根据HTTP标准,HTTP请求可以使用多种请求方法。
HTTP1.0定义了三种请求方法: GET, POST 和 HEAD方法。
HTTP1.1新增了五种请求方法:OPTIONS, PUT, DELETE, TRACE 和 CONNECT 方法。
GET 请求指定的页面信息,并返回实体主体。
HEAD 类似于get请求,只不过返回的响应中没有具体的内容,用于获取报头
POST 向指定资源提交数据进行处理请求(例如提交表单或者上传文件)。数据被包含在请求体中。POST请求可能会导致新的资源的建立和/或已有资源的修改。
PUT 从客户端向服务器传送的数据取代指定的文档的内容。
DELETE 请求服务器删除指定的页面。
CONNECT HTTP/1.1协议中预留给能够将连接改为管道方式的代理服务器。
OPTIONS 允许客户端查看服务器的性能。
TRACE 回显服务器收到的请求,主要用于测试或诊断。9.HTTP工作原理
HTTP协议定义Web客户端如何从Web服务器请求Web页面,以及服务器如何把Web页面传送给客户端。HTTP协议采用了请求/响应模型。客户端向服务器发送一个请求报文,请求报文包含请求的请求头部方法、URL、协议版本、和请求数据。服务器以一个状态行作为响应,响应的内容包括协议的版本、成功或者错误代码、服务器信息、响应头部和响应数据。
以下是 HTTP 请求/响应的步骤:
1、客户端连接到Web服务器
一个HTTP客户端,通常是浏览器,与Web服务器的HTTP端口(默认为80)建立一个TCP套接字连接。例如,http://www.oakcms.cn。
2、发送HTTP请求
通过TCP套接字,客户端向Web服务器发送一个文本的请求报文,一个请求报文由请求行、请求头部、空行和请求数据4部分组成。
3、服务器接受请求并返回HTTP响应
Web服务器解析请求,定位请求资源。服务器将资源复本写到TCP套接字,由客户端读取。一个响应由状态行、响应头部、空行和响应数据4部分组成。
4、释放连接TCP连接
若connection 模式为close,则服务器主动关闭TCP连接,客户端被动关闭连接,释放TCP连接;若connection 模式为keepalive,则该连接会保持一段时间,在该时间内可以继续接收请求;
5、客户端浏览器解析HTML内容
客户端浏览器首先解析状态行,查看表明请求是否成功的状态代码。然后解析每一个响应头,响应头告知以下为若干字节的HTML文档和文档的字符集。客户端浏览器读取响应数据HTML,根据HTML的语法对其进行格式化,并在浏览器窗口中显示。
例如:在浏览器地址栏键入URL,按下回车之后会经历以下流程:
1、浏览器向 DNS 服务器请求解析该 URL 中的域名所对应的 IP 地址;
2、解析出 IP 地址后,根据该 IP 地址和默认端口 80,和服务器建立TCP连接;
3、浏览器发出读取文件(URL 中域名后面部分对应的文件)的HTTP 请求,该请求报文作为 TCP 三次握手的第三个报文的数据发送给服务器;
4、服务器对浏览器请求作出响应,并把对应的 html 文本发送给浏览器;
5、释放 TCP连接;
6、浏览器将该 html 文本并显示内容;
10.GET和POST请求的区别
GET请求
GET /books/?sex=man&name=Professional HTTP/1.1
Host: www.wrox.com
User-Agent: Mozilla/5.0 (Windows; U; Windows NT 5.1; en-US; rv:1.7.6)
Gecko/20050225 Firefox/1.0.1
Connection: Keep-Alive注意最后一行是空行
POST请求
POST / HTTP/1.1
Host: www.wrox.com
User-Agent: Mozilla/5.0 (Windows; U; Windows NT 5.1; en-US; rv:1.7.6)
Gecko/20050225 Firefox/1.0.1
Content-Type: application/x-www-form-urlencoded
Content-Length: 40
Connection: Keep-Alivename=Professional%20Ajax&publisher=Wiley1、GET提交,请求的数据会附在URL之后(就是把数据放置在HTTP协议头中),以?分割URL和传输数据,多个参数用&连接;例 如:login.action?name=hyddd&password=idontknow&verify=%E4%BD%A0 %E5%A5%BD。如果数据是英文字母/数字,原样发送,如果是空格,转换为+,如果是中文/其他字符,则直接把字符串用BASE64加密,得出如: %E4%BD%A0%E5%A5%BD,其中%XX中的XX为该符号以16进制表示的ASCII。
POST提交:把提交的数据放置在是HTTP包的包体中。上文示例中红色字体标明的就是实际的传输数据
因此,GET提交的数据会在地址栏中显示出来,而POST提交,地址栏不会改变
2、传输数据的大小:首先声明:HTTP协议没有对传输的数据大小进行限制,HTTP协议规范也没有对URL长度进行限制。
而在实际开发中存在的限制主要有:
GET:特定浏览器和服务器对URL长度有限制,例如 IE对URL长度的限制是2083字节(2K+35)。对于其他浏览器,如Netscape、FireFox等,理论上没有长度限制,其限制取决于操作系 统的支持。
因此对于GET提交时,传输数据就会受到URL长度的 限制。
POST:由于不是通过URL传值,理论上数据不受 限。但实际各个WEB服务器会规定对post提交数据大小进行限制,Apache、IIS6都有各自的配置。
3、安全性
POST的安全性要比GET的安全性高。比如:通过GET提交数据,用户名和密码将明文出现在URL上,因为(1)登录页面有可能被浏览器缓存;(2)其他人查看浏览器的历史纪录,那么别人就可以拿到你的账号和密码了,除此之外,使用GET提交数据还可能会造成Cross-site request forgery攻击
4、Http get,post,soap协议都是在http上运行的
(1)get:请求参数是作为一个key/value对的序列(查询字符串)附加到URL上的
查询字符串的长度受到web浏览器和web服务器的限制(如IE最多支持2048个字符),不适合传输大型数据集同时,它很不安全
(2)post:请求参数是在http标题的一个不同部分(名为entity body)传输的,这一部分用来传输表单信息,因此必须将Content-type设置为:application/x-www-form- urlencoded。post设计用来支持web窗体上的用户字段,其参数也是作为key/value对传输。
但是:它不支持复杂数据类型,因为post没有定义传输数据结构的语义和规则。
(3)soap:是http post的一个专用版本,遵循一种特殊的xml消息格式
Content-type设置为: text/xml 任何数据都可以xml化。
Http协议定义了很多与服务器交互的方法,最基本的有4种,分别是GET,POST,PUT,DELETE. 一个URL地址用于描述一个网络上的资源,而HTTP中的GET, POST, PUT, DELETE就对应着对这个资源的查,改,增,删4个操作。 我们最常见的就是GET和POST了。GET一般用于获取/查询资源信息,而POST一般用于更新资源信息.
我们看看GET和POST的区别
-
-
GET提交的数据会放在URL之后,以?分割URL和传输数据,参数之间以&相连,如EditPosts.aspx?name=test1&id=123456. POST方法是把提交的数据放在HTTP包的Body中.
-
GET提交的数据大小有限制(因为浏览器对URL的长度有限制),而POST方法提交的数据没有限制.
-
GET方式需要使用Request.QueryString来取得变量的值,而POST方式通过Request.Form来获取变量的值。
-
GET方式提交数据,会带来安全问题,比如一个登录页面,通过GET方式提交数据时,用户名和密码将出现在URL上,如果页面可以被缓存或者其他人可以访问这台机器,就可以从历史记录获得该用户的账号和密码.
-
