快手评论点赞网站建设专业分站wordpress两个菜单栏
在计算机科学中,排序算法是基础且重要的主题之一。选择排序(Selection Sort)是其中一个简单但非常有用的排序算法。本文将详细介绍选择排序的原理和步骤,并提供Java语言的实现示例。

选择排序的原理
选择排序的核心思想是不断地从待排序的元素中选择最小的元素,然后将其放置在已排序部分的末尾。它的过程类似于人们在扑克牌中不断选择最小的牌并将其放置在手中的已排序牌的最后一张。这个过程重复进行,直到所有牌都被排序完毕。
选择排序的步骤
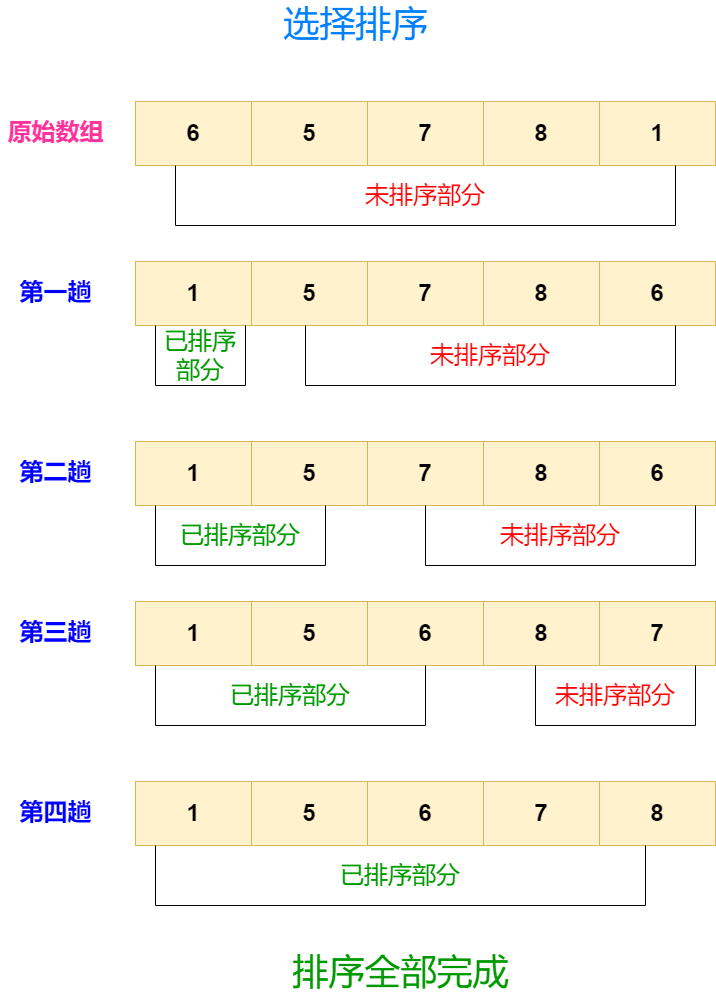
选择排序的步骤可以简单概括为以下几个阶段:
-
初始状态: 将整个数组视为未排序的部分。
-
第一次选择: 从未排序部分选择最小的元素,并将其与未排序部分的第一个元素交换位置。此时,第一个元素被视为已排序的一部分,而其余部分是未排序的。
-
第二次选择: 从剩余未排序部分选择最小的元素,并将其与未排序部分的第一个元素交换位置。现在,前两个元素被视为已排序的一部分,而其余部分是未排序的。
-
重复: 重复上述选择和交换的过程,每次选择并交换一个最小的元素,直到整个数组变为已排序状态。
-
完成: 当算法完成时,整个数组都已排序。
Java代码选择排序
以下是使用Java语言实现选择排序算法的示例代码:
public class Test {public static void main(String[] args) {int[] arr = new int[]{5,2,4,6,7,1,3};selectionSort(arr);}public static void selectionSort(int[] arr){System.out.println("原始数组:"+ Arrays.toString(arr));//获取数组长度int len = arr.length;//循环len-1次,进行数组排序,没排序完一趟,则从下标为i的元素及之后的元素为未排序的部分for(int i = 0; i< len-1; i++){//默认未排序的部分的第一个元素为最小元素下标int minIndex = i;//循环未排序的部分的数组,找出最小6元素的下标for(int j = i+1; j < len; j++){if(arr[j] < arr[minIndex]){minIndex = j;}}//将最小元素与未排序的部分的数组的第一个元素交换int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;// 打印每趟排序完成后的数组状态,以便查看排序进度System.out.println("第"+(i+1)+"趟排序完成的数组:"+ Arrays.toString(arr));}System.out.println("排序完成的数组:"+ Arrays.toString(arr));}
}打印结果为:
原始数组:[5, 2, 4, 6, 7, 1, 3]
第1趟排序完成的数组:[1, 2, 4, 6, 7, 5, 3]
第2趟排序完成的数组:[1, 2, 4, 6, 7, 5, 3]
第3趟排序完成的数组:[1, 2, 3, 6, 7, 5, 4]
第4趟排序完成的数组:[1, 2, 3, 4, 7, 5, 6]
第5趟排序完成的数组:[1, 2, 3, 4, 5, 7, 6]
第6趟排序完成的数组:[1, 2, 3, 4, 5, 6, 7]
排序完成的数组:[1, 2, 3, 4, 5, 6, 7]
以上代码演示了如何使用选择排序对一个整数数组进行排序。选择排序算法虽然不如一些高级排序算法快速,但它易于理解和实现,对于小型数据集或接近排序状态的数据集可能是一个合理的选择。
总结
选择排序虽然不是最高效的排序算法,但它是一个简单而直观的例子,有助于理解排序算法的基本原理。希望本文的解释和示例有助于您更好地理解选择排序,并在需要时应用它来解决排序问题。
