好看的免费网站模板下载 迅雷下载地址上传网站中ftp地址写什么
proteus8.15版本可以用STM32系列单片机来进行仿真设计,比7.8版本方便多了,有需要的朋友们可以在公众号后台回复 proteus8.15 获取软件包。

1、下载好软件包,解压如下,右键proteus8.15.sp1以管理员身份运行。

2、第一次安装,会提示安装如下的环境,不用惊讶,点击next。

3、按顺序来,最后点击install。

4、点击finish。

5、点击next。

6、按步骤1.2顺序来。
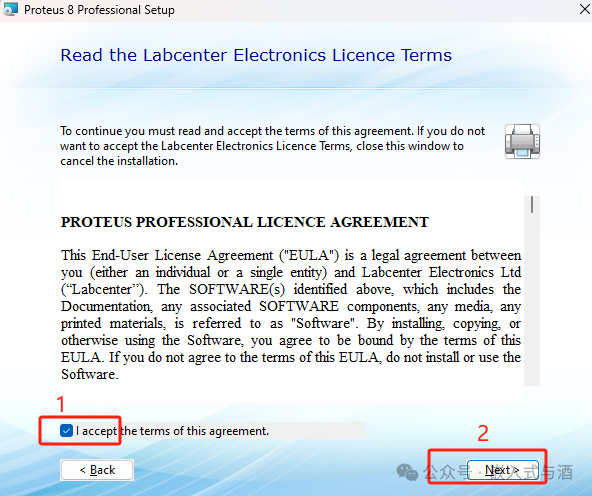
7、默认即可。

8、点击next

9、点击brown for key file

10、来到软件包目录下的fix文件夹下,选中这个文件,并打开它。

11、点击install

12、点击“是”。

13、点击close。

14、点击next。
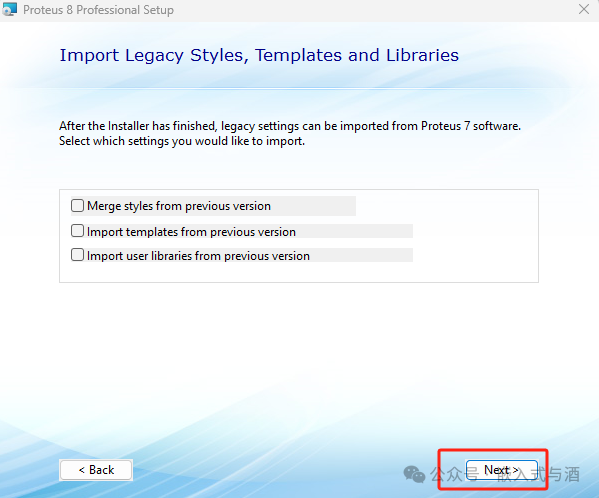
15、选择Custom自定义安装目录,建议选择自定义哦。

16、按照步骤1、2、3来操作你的自定义目录哦。

17、点击next。

18、点击next。

19、点击install,进行软件的安装。

20、安装过程中......很快滴。

21、安装完成,点击close,不要Run。

22、来到Fix文件夹下,双击它。

23、点击OK。

24、点击start。

25、出现框起来的successful,即破解完成。

26、回到桌面,双击打开proteus8.15的图标,安装完成了。
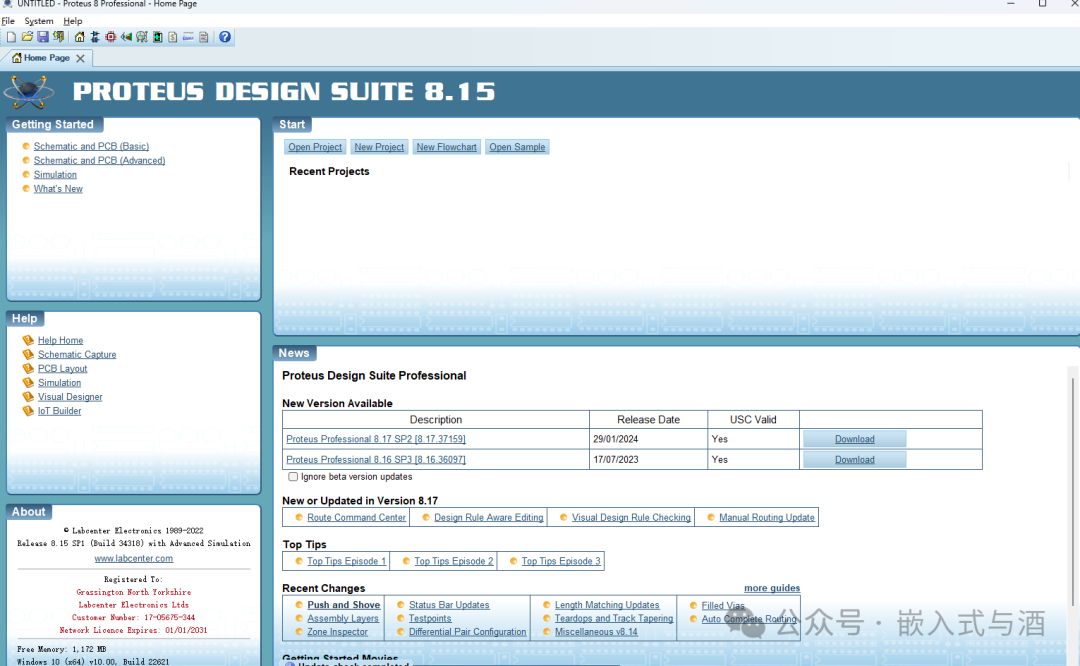
27、打开一个STM32,LED仿真例程。

