网站建设公司宣传册网站建设规划书企业网站
UltraISO下载
下载链接:https://pan.baidu.com/s/18ukDs6yL64qU6thYyZEo-Q?pwd=o8he
提取码:o8he
一路傻瓜安装,安装后点击继续试用

Ubuntu系统下载
这里我使用的是官网的22.04版本,由于大于4G,无法上传至百度网盘,这里就不给连接了,底下图片是18.04的,没装好,但留有截图,22.04步骤相同
U盘刻录
打开UltraISO,点击文件 - > 打开,选择Ubuntu系统。
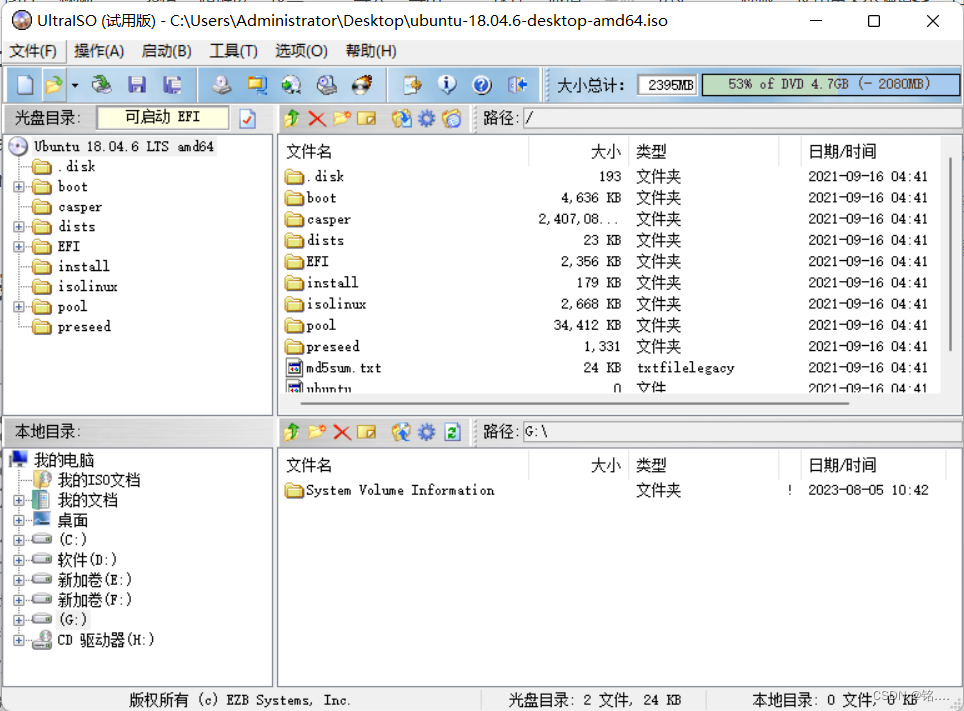
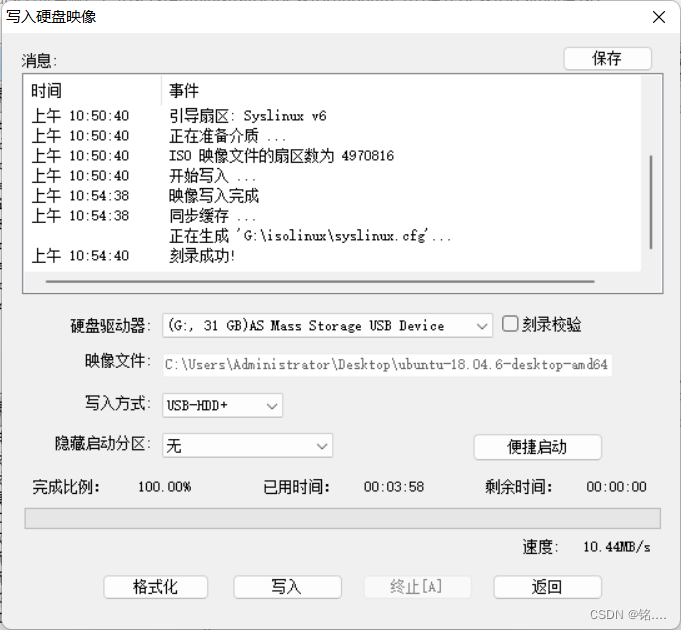
插入u盘,启动 -> 写入硬盘映像 -> 写入
写入完成如下所示
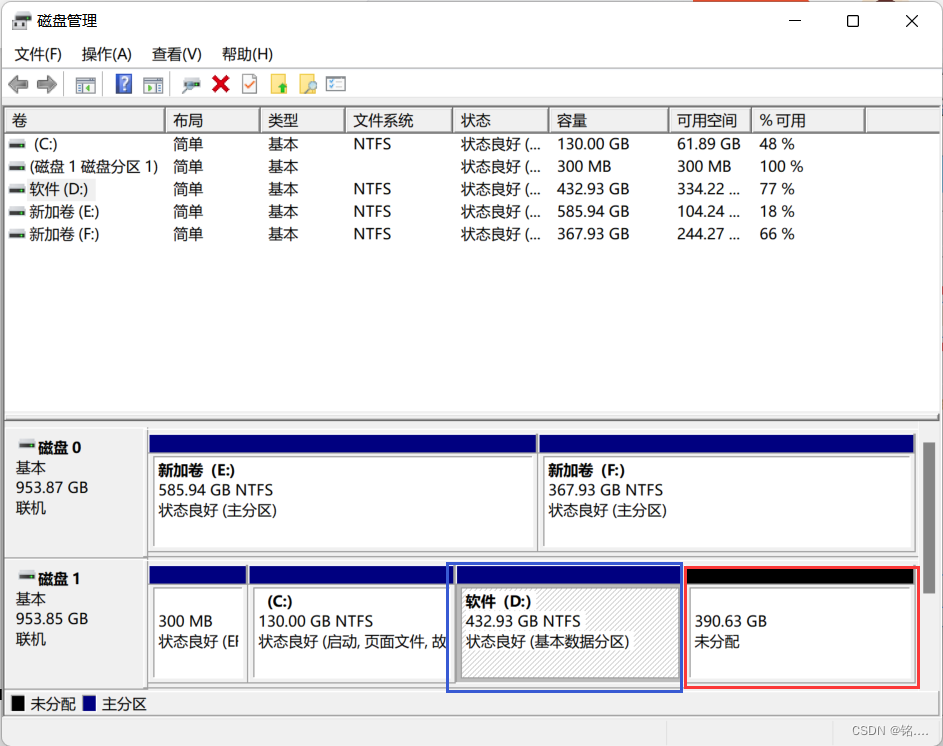
硬盘压缩
打开磁盘管理,右键如蓝框部分,点击压缩卷,设定所需大小,压缩后出现如红框所示空间,后来发现空间留大了,改为200G,这里仅为步骤参考,有人说120G也行,看个人了
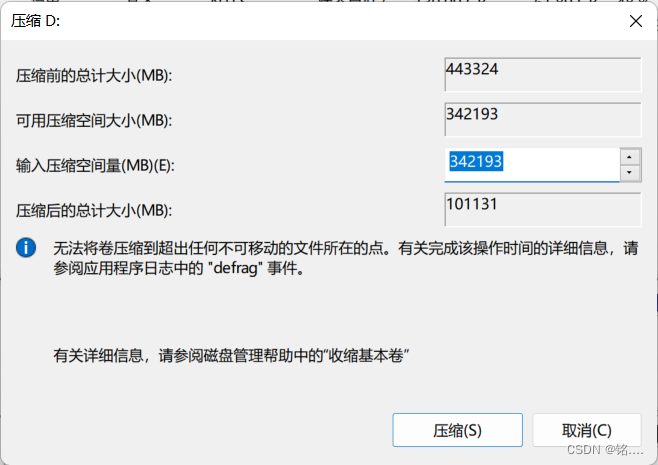
设置BIOS
由于设置BIOS时无法截图,以下均没有图片,见谅
本人宏碁掠夺者neo,在开机时不停按F2进入BIOS,其他电脑自行查询如何进入BIOS
进入BIOS后,在boot中设置从u盘启动,退出后重启电脑,如无意外,可进入ubuntu系统安装
后面的过程可参照这篇博客
https://blog.csdn.net/m0_51233386/article/details/114264254?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169139159516800222866878%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=169139159516800222866878&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduend~default-1-114264254-null-null.142v92insert_down28v1&utm_term=window%E4%B8%8Eubantu%E5%8F%8C%E7%B3%BB%E7%BB%9F&spm=1018.2226.3001.4187
