凡科建设网站入门版好不万网网站多少
「发表于知乎专栏《移动端算法优化》」
本文主要介绍了 NEON 指令相关的知识,首先通过讲解 arm 指令集的分类,NEON寄存器的类型,树立基本概念。然后进一步梳理了 NEON 汇编以及 intrinsics 指令的格式。最后结合指令的分类,使用例子讲述 NEON 指令的使用方法。
🎬个人简介:一个全栈工程师的升级之路!
📋个人专栏:高性能(HPC)开发基础教程
🎀CSDN主页 发狂的小花
🌄人生秘诀:学习的本质就是极致重复!
目录
一、 概述
二、NEON指令格式
2.1 Armv7,Armv8,Armv9的介绍
2.2 向量寄存器介绍
2.2.1 AArch64 向量寄存器
2.2.2 AArchh32 / ARMV7向量寄存器
2.3 汇编指令格式介绍
2.3.1 AArch64汇编指令格式
2.3.2 AArch32 / Armv7汇编指令格式
2.4 intrinsics指令格式
2.4.1 向量类型格式
2.4.2 NEON内联函数格式
三、intrinsics 指令介绍
3.1 intrinsics指令分类
3.2 NEON intrinsics指令详述
3.2.1 Load/Store
3.2.2 Arithmetic
3.2.3 Multiply
3.2.4 Shift
3.2.5 Logical and compare
3.2.6 Floating-point
3.2.7 Permutation
3.2.8 Miscellaneous
3.2.9 Data processing
3.2.10 Type conversion
四、NEON intrisics 指令在x86平台的仿真
五、 NEON指令的应用
5.1 RGB de-interleave 加载 / interleave 存储
5.2 查表操作
5.3 边缘处理
5.4 SAD操作
六、总结
一、 概述
ARM NEON 可以提升计算机视觉等计算密集型程序的性能,编译器可以将 C/C++ 代码自动转换为 NEON 指令。但是想要有更好的性能还是需要手工编写 NEON 代码,熟练掌握 NEON 指令是第一步。
本文接下来会详细的介绍 Armv7 和 Armv8 架构下 NEON 向量寄存器、NEON 汇编指令格式、NEON Intrinsics 指令格式、常用的 Intrinsics 指令以及作用、在 x86 平台调试 NEON 代码,最后针对几个常用的 Intrinsics 指令结合实例进行说明。
二、NEON指令格式
2.1 Armv7,Armv8,Armv9的介绍
Armv7-A 和 Armv8-A 的关系如下图所示:

ARM ISA
Armv8-A 的执行状态可以分为 AArch64 和 AArch32 两种状态。
- AArch64 是 64 位执行状态,支持 A64 指令集。
- AArch32 是 32 位执行状态,支持 T32 和 A32 指令集,同时 AArch32 与 AArch64 中一些的功能保持一致,而且 AArch32 兼容 Armv7-A。
ARMV8 支持浮点类型的除法向量操作,这是ARMV7所没有的。另外AArch64还支持double类型的操作。
Armv9-A 是 arm 当前最新的指令架构,Armv9-A 除了向前兼容 Armv8-A,在性能计算上有了很大的提升,主要表现在安全、AI 以及改进矢量扩展(SVE2)和 DSP 能力。
2.2 向量寄存器介绍
向量寄存器用来存放向量数据,每个向量元素的类型必须相同。向量寄存器根据处理元素的大小可以划分为 2/4/8/16 个通道。

SIMD register
2.2.1 AArch64 向量寄存器
AArch64 有 32 个 128bit 的向量寄存器,这些寄存器又可以划分为:
- 32 个 128bit 的 V 寄存器,V0~V31。
- 32 个 64bit 的 D 寄存器,D0~D31。
- 32 个 32bit 的 S 寄存器,S0~S31。
每种类型寄存器的映射关系如下:

AArch64 SIMD register
2.2.2 AArchh32 / ARMV7向量寄存器
AArch32/Armv7 有 16 个 128bit 的向量寄存器,这些寄存器又可以划分为:
- 16 个128bit 的 Q 寄存器,Q0~Q15。
- 32 个 64bit 的 D 寄存器,D0~D31。
- 32 个 32bit 的 S 寄存器,S0~S31。
每种类型寄存器的映射关系如下:

AArch32 SIMD register
2.3 汇编指令格式介绍
AArch64 与AArch32 / Armv7-A 的 NEON 汇编指令除了种类上存在差异,格式上也存在很大差异。
其中指令中有一些通用的书写格式, 含义如下:
- {}, 表示可选项
- <>, 表示必选项
2.3.1 AArch64汇编指令格式
{<prefix>}<op>{<suffix>} Vd.<T>, Vn.<T>, Vm.<T>1)<prefix> 表示前缀名字,包括以下几类:
- S/U/F/P:表示数据类型,分别为 有符号整型/无符号整型/浮点型/布尔型。
- Q:表示饱和(Saturating)计算。
- R:表示舍入(Rounding)计算, Rounding 操作等价于加上 0.5 之后再截断。
- H:表示折半(Halving)计算。
- D:表示翻倍(Doubling)算。
2)<op> 表示具体的操作,例如 ADD,SUB 等等
3)<suffix> 表示后缀名字,包括以下几类:
- V:表示 Reduction 计算。
- P:表示 Pairwise 计算。
- H:表示结果只取每个通道的高半部分(High)。
- L/N/W/L2/N2/W2:表示数据长度的变化
- L / L2 :表示输出向量是输入向量长度的 2 倍,其中 L 表示输入寄存器的低 64bit 数据有效,L2 表示输入寄存器的高 64bit 数据有效。

L/L2
-
- N/N2:表示输出向量是输入向量的 1/2 倍,N 表示输出向量只有低 64bit 有效,N2 则表示输出向量只有高 64bit 有效。

N/N2
-
- W/W2:表示输出向量和第一个输入向量长度相等,且这两个向量是第二个向量长度的 2 倍,其中 W 表示第二个输入向量的低 64bit 有效,W2 表示第二输入向量的高 64bit 有效。

W/W2
4)<T> 表示单个通道的数据类型,8B/16B/4H/8H/2S/4S/2D,B 表示 8bit,H 表示 16bit,S 表示 32bit,D 表示 64bit。
- 汇编指令例子
SQRSHRN2 表示对向量进行 Rouding 类型的右移操作,并对结果做饱和计算,最后将结果赋给目的向量的高半部分,并保持低半部分不改变,具体示例如下
// 指令语句作用:
// 将 V2 向量中每个元素按照 Rounding 方式右移动 2 位,然后对结果做饱和操作,
// 并将结果保存到V0上半部分,而且保证V0的下半部分保持不变
// 指令格式说明:
// S -- 表示有符号操作
// Q -- 表示饱和操作
// R -- 表示舍入操作
// SHR -- 表示向右位移
// N2 -- 表示将结果保存到输出向量的高 64bit
// V2.2D -- 表示输入向量寄存器,长度为 128bit,一共两个通道,每个通道 64bit
// V0.4S -- 表示输出向量寄存器,长度为 128bit,一共四个通道,每个通道 32bitSQRSHRN2 V0.4S,V2.2D,2// 伪代码如下:
int shift = 2;
int round_const = (1 << (shift - 1));
V0[2] = SAT((V2[0] + round_const) >> shift)
V0[3] = SAT((V2[1] + round_const) >> shift)

SQRSHRN2
2.3.2 AArch32 / Armv7汇编指令格式
V{<mod>}<op>{<shape>}{<cond>}{.<dt>}<dest1>{,<dest2>},<src1>{,<src2>}1)V AArch32 / Armv7 的汇编指令以"V"开头
2)<mod> 该修饰字可以表示为以下类型:
- Q, 表示饱和(Saturating)计算。
- R, 表示舍入(Rounding)计算,Rounding 操作等价于加上 0.5 之后再截断。
- H, 表示折半(Halving)计算。
- D, 表示翻倍(Doubling)计算。
3)<op> 表示具体的操作,例如 ADD,SUB等等
4)<shape> 表示数据长度的变化,L/N/W。
5)<cond> 表示指令执行的条件
6).<dt> 表示数据类型,默认为第二个操作数的数据类型。如果第二个操作数不存在,为第一个操作数类型,仍不存在为结果操作数类型。
7)<dest> 表示输出操作数
8)<src1> <src2>表示两个输入操作数
汇编指令例子
VQDMULL 表示两向量相乘,结果乘以 2。
// 指令语句作用:
// 64bit 向量 D1 和 D3 中每个元素对应相乘,并将结果乘以 2
// 最后的结果做饱和之后赋值给 128bit 向量 Q0
//
// 指令格式说明:
// Q -- 表示饱和操作
// D -- 表示 doubling 操作,即乘以 2
// MUL -- 表示乘法操作
// L -- 输出向量是输入向量长度的 2 倍
// .S16 -- 表示操作元素的数据类型为有符号 16bit
// Q0 -- 表示输出向量寄存器,长度为 128bit
// D1 -- 表示输入向量寄存器,长度为 64bit
// D3 -- 表示输入向量寄存器,长度为 64bitVQDMULL.S16 Q0, D1, D3// 伪代码
for (int i = 0; i < 4; i++)
{q0[i] = SAT(d1[i] * d3[i] * 2)
}

VQDMULL.S16
2.4 intrinsics指令格式
相比于汇编指令,NEON Intrinsics 是一种更简单的编写 NEON 代码的方法,NEON Intrinsics 类似于 C 函数调用,在编译时由编译器替换为相应的汇编指令,使用时需要包含头文件arm_neon.h。
2.4.1 向量类型格式
// 非数组向量格式
<type><size>x<number_of_lanes>_t
// 数组向量格式
<type><size>x<number_of_lanes>x<length_of_array>_t
1)<type> 数据类型,如 int/uint/float/poly。
2)<size> 元素大小,如8/16/32/64。
3) <number_of_lanes> 通道数。
4) <length_of_array> 数组中元素个数。

向量类型示意图
2.4.2 NEON内联函数格式
v<mod><opname><shape><flags>_<type>
1)<mod>
- q:表示饱和计算,例如
// a加b的结果做饱和计算
int8x8_t vqadd_s8(int8x8_t a, int8x8_t b);
- h:表示折半计算,例如
// a减b的结果右移一位
int8x8_t vhsub_s8(int8x8_t a, int8x8_t b);
- d:表示加倍计算,例如
// a乘b的结果扩大一倍, 最后做饱和操作
int32x4_t vqdmull_s16(int16x4_t a, int16x4_t b);
- r:表示舍入计算,例如
// 将a与b的和减半,同时做rounding 操作, 每个通道可以表达为: (ai + bi + 1) >> 1
int8x8_t vrhadd_s8(int8x8_t a, int8x8_t b);
- p:表示pairwise计算。例如
// 将a, b向量的相邻数据进行两两和操作
int8x8_t vpadd_s8(int8x8_t a, int8x8_t b);
2) <opname> 表示具体操作,比如 add,sub。
3) <shape>
- l:表示long,输出向量的元素长度是输入长度的2倍,例如
uint16x8_t vaddl_u8(uint8x8_t a, uint8x8_t b);
- n:表示 narrow,输出向量的元素长度是输入长度的1/2倍,例如
uint32x2_t vmovn_u64(uint64x2_t a);
- w:表示 wide,第一个输入向量和输出向量类型一样,且是第二个输入向量元素长度的2倍,例如
uint16x8_t vsubw_u8(uint16x8_t a, uint8x8_t b);
- _high:AArch64专用,而且和 l/n 配合使用。
- 当使用 l(Long) 时,表示输入向量只有高 64bit 有效;
- 当使用 n(Narrow) 时,表示输出只有高 64bit 有效。
// a 和 b 只有高 64bit 参与运算
int16x8_t vsubl_high_s8(int8x16_t a, int8x16_t b);
- _n:表示有标量参与向量计算,例如
// 向量 a 中的每个元素右移 n 位
int8x8_t vshr_n_s8(int8x8_t a, const int n);
- _lane: 指定向量中某个通道参与向量计算,例如
// 取向量 v 中下标为 lane 的元素与向量 a 做乘法计算
int16x4_t vmul_lane_s16(int16x4_t a, int16x4_t v, const int lane);
4) <flags>
- q:表示使用 128bit 的向量,否则使用 64bit 的向量。
5) <type> 表示单个通道的数据类型,有u8、s8、u16、s16、u32、s32、f32、f64。

内联函数结构示意图
三、intrinsics 指令介绍
3.1 intrinsics指令分类
| 功能类别 | 介绍 |
|---|---|
| Load/Store | 对数据进行向量加载和存储,既可以对单个数据进行加载和存储,也可以对向量结构体数据进行加载和存储 |
| Arithmetic | 对整数和浮点数向量加减运算 |
| Multiply | 整型或浮点型的向量乘法运算,同时包含了乘法和加法混合运算,以及乘法和减法的运算的混合运算 |
| Shift | 向量位移操作,其中位移数据可以是立即数也可以是向量 |
| Logical and compare | 包含了逻辑运算(与或非运算等)和比较运算(等于、大于、小于等) |
| Floating-point | 包含了浮点和其他类型数据之间的相互转化操作 |
| Permutation | 对向量进行重排操作 |
| Misecllaneous | 标量数据赋值到向量的操作 |
| Data processing | 一般性处理,极值操作、绝对值差、数值取反、平方根倒数等 |
| Type conversion | 数值类型转换,数据的组合及提取等 |
3.2 NEON intrinsics指令详述
本节将对每种类型的 NEON intrinsics 指令做出详细的描述。
3.2.1 Load/Store
- 以解交织的方式加载数据
// 以解交织方式加载数据到n个向量寄存器, n为1~4
Result_t vld[n]<q>_type(Scalar_t *p_addr);// 以解交织方式加载数据到n个向量寄存器的第N通道, n为1~4
Result_t vld[n]<q>_lane_type(Scalar_t *p_addr, Vector_t M, int N);
- 以交织的方式存储数据
// 将n个向量寄存器数据以交织方式存储到内存中, n为1~4
void vst[n]<q>_type(Scalar_t* N, Vector_t M);// 将n个寄存器的N通道数据以交织方式存储到内存中, n为1~4
void vst[n]<q>_lane_type(Scalar_t *p_addr, Vector_t M, int N);

2 个向量中多通道 load/store, 以及单个通道的load/store
3.2.2 Arithmetic
- 整数和浮点数的加减运算。
// 基本的加减操作
Result_t vadd<q>_type(Vector1_t N, Vector2_t M);
Result_t vsub<q>_type(Vector1_t N, Vector2_t M);// L(Long)类型的指令加减运算,输出向量长度是输入的两倍。
Result_t vaddl_type(Vector1_t N, Vector2_t M);
Result_t vsubl_type(Vector1_t N, Vector2_t M);// W(Wide)类型的指令加减运算,第一个输入向量的长度是第二个输入向量长度的两倍。
Result_t vaddw_type(Vector1_t N, Vector2_t M);
Result_t vsubw_type(Vector1_t N, Vector2_t M);// H(half)类型的加减运算;将计算结果除以2。
Result_t vhadd<q>_type(Vector1_t N, Vector2_t M);
Result_t vhsub<q>_type(Vector1_t N, Vector2_t M);// Q(Saturated)饱和类型的加减操作
Result_t vqadd<q>_type(Vector1_t N, Vector2_t M);
Result_t vqsub<q>_type(Vector1_t N, Vector2_t M);// RH(Rounding Half)类型的加减运算
Result_t vrhadd<q>_type(Vector1_t N, Vector2_t M);
Result_t vrhsub<q>_type(Vector1_t N, Vector2_t M);// HN(half Narrow)类型的加减操作
Result_t vaddhn_type(Vector1_t N, Vector2_t M);
Result_t vsubhn_type(Vector1_t N, Vector2_t M);// RHN(rounding half Narrow)类型的加减操作
Result_t vraddhn_type(Vector1_t N, Vector2_t M);
Result_t vrsubhn_type(Vector1_t N, Vector2_t M);

vhadd_s32 instrisics指令的操作
3.2.3 Multiply
- 整型和浮点型的乘法运算, 参与计算的都是向量
// 基本乘法操作
Result_t vmul<q>_type(Vector1_t N, Vector2_t M);// l(Long)类型的乘法操作
Result_t vmull_type(Vector1_t N, Vector2_t M);// QDL(Saturated, Double, Long)类型的乘法操作
Result_t vqdmull_type(Vector1_t N, Vector2_t M);// 基本的乘加和乘减操作
Result_t vmla<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);
Result_t vmls<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);// L(Long)类型的乘加和乘减操作
Result_t vmlal_type(Vector1_t N, Vector2_t M, Vector3_t P);
Result_t vmlsl_type(Vector1_t N, Vector2_t M, Vector3_t P);// QDL(Saturated, Double, Long)类型的乘加和乘减操作
Result_t vqdmlal_type(Vector1_t N, Vector2_t M, Vector3_t P);
Result_t vqdmlsl_type(Vector1_t N, Vector2_t M, Vector3_t P);// QDLH(Saturated, Double, Long, Half)类型的乘法操作
Result_t vqdmulh<q>_type(Vector1_t N, Vector2_t M);// QRDLH(Saturated, Rounding Double, Long, Half)类型的乘法操作
Result_t vqrdmulh<q>_type(Vector1_t N, Vector2_t M);
- 带通道类型的乘法操作
// 基本的乘法操作
Result_t vmull_lane_type(Vector1_t N, Vector2_t M, int n);// 基本的乘加和乘减操作
Result_t vmla<q>_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);
Result_t vmls<q>_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);// L(long) 类型的乘加和乘减操作
Result_t vmlal_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);
Result_t vmlsl_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);// QDL(Saturated, Double, long) 类型的乘加和乘减操作
Result_t vqdmlal_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);
Result_t vqdmlsl_lane_type(Vector1_t N, Vector2_t M, Vector3_t P, int n);// QDH(Saturated, Double, Half) 类型的操作
Result_t vqdmulh<q>_lane_type(Vector1_t N, Vector2_t M, int n);

vmla_lane_s32 intrinsics 指令的操作
- 向量和标量的乘法
// 基本的向量和标量的乘法
Result_t vmul<q>_n_type(Vector_t N, Scalar_t M);// L(Long) 类型的向量和标量的乘法
Result_t vmull_n_type(Vector_t N, Scalar_t M);// QDL(Saturated, Double, long) 类型的向量和标量的乘法
Result_t vqdmull_n_type(Vector_t N, Scalar_t M);// QDH(Saturated, Double, Half) 类型的向量和标量的乘法
Result_t vqdmulh<q>_n_type(Vector_t N, Scalar_t M);// QRDH(Saturated, Double, Half) 类型的向量和标量的乘法
Result_t vqrdmulh<q>_n_type(Vector_t N, Scalar_t M);// L(Long) 类型的乘加和乘减操作
Result_t vmlal_n_type(Vector1_t N, Vector2_t M, Scalar_t P);
Result_t vmlsl_n_type(Vector1_t N, Vector2_t M, Scalar_t P);// QDL(Saturated, Double, long) 类型的乘加和乘减
Result_t vqdmlal_n_type(Vector1_t N, Vector2_t M, Scalar_t P);
Result_t vqdmlsl_n_type(Vector1_t N, Vector2_t M, Scalar_t P);
3.2.4 Shift
- 立即数类型的位移
// 基本的立即数左移和右移
Result_t vshr<q>_n_type(Vector_t N, int n);
Result_t vshl<q>_n_type(Vector_t N, int n);// R(rounding) 类型的右移操作
Result_t vrshr<q>_n_type(Vector_t N, int n);// QL(Saturated, long) 类型的右移操作
Result_t vqshl<q>_n_type(Vector_t N, int n);// 右移累加操作
Result_t vsra<q>_n_type(Vector1_t N, Vector2_t M, int n);// R(rounding) 类型的右移累加操作
Result_t vrsraq_n_type(Vector1_t N, Vector2_t M, int n);// Q(Saturated) 类型的左移操作,而且输入是有符号,输出是无符号的
Result_t vqshluq_n_type(Vector_t N, int n);// N(Narrow) 类型的右移操作
Result_t vshrn_n_type(Vector_t N, int n);// QN(Saturated, Narrow) 类型的右移操作, 而且输入是有符号,输出是无符号的
Result_t vqshrun_n_type(Vector_t N, int n);// QRN(Saturated, Rounding, Narrow) 类型的右移操作, 而且输入是有符号,输出是无符号的
Result_t vqrshrun_n_type(Vector_t N, int n);// QN(Saturated, Narrow) 类型的右移操作
Result_t vqshrn_n_type(Vector_t N, int n);// RN(Rounding, Narrow) 类型的右移操作
Result_t vrshrn_n_type(Vector_t N, int n);// QRN(Rounding, Rounding, Narrow) 类型的右移操作
Result_t vqrshrn_n_type(Vector_t N, int n);// N(Narrow) 类型的左移操作
Result_t vshll_n_type(Vector_t N, int n);
- 非立即数类型的位移
// 左移
Result_t vshlq_type(Vector1_t N, Vector2_t M);// Q(Saturated) 类型的左移操作
Result_t vqshl<q>_type(Vector1_t N, Vector2_t M);// QR(Saturated, rounding) 类型的左移操作
Result_t vrshl<q>_type(Vector1_t N, Vector2_t M);
- 移位并插入
// 将向量 M 中各个通道先右移动 n 位, 然后将移动后元素插入到 N 对应的元素中,
// 并保持 N 中每个元素的高 n 位保持不变
Result_t vsri<q>_n_type(Vector1_t N, Vector2_t M, int n);// 将向量 M 中各个通道先左移动 n 位, 然后将移动后元素插入到 N 对应的元素中,
// 并保持 N 中第每个元素的低 n 位保持不变
Result_t vsli<q>_n_type(Vector1_t N, Vector2_t M, int n);

vsliq_n_u32 intrinsics 指令的操作
3.2.5 Logical and compare
eq 表示相等, ge 表示大于或等于, gt 表示大于, le 表示小于或等于, lt 表示小于
- 逻辑比较操作,比较结果为true,输出向量的对应通道将被设置为全 1,否则设置为全0 。
Result_t vceq<q>_type(Vector1_t N, Vector2_t M);
Result_t vcge<q>_type(Vector1_t N, Vector2_t M);
Result_t vcle<q>_type(Vector1_t N, Vector2_t M);
Result_t vcgt<q>_type(Vector1_t N, Vector2_t M);
Result_t vclt<q>_type(Vector1_t N, Vector2_t M);
- 向量的绝对值比较,比较结果为true时,输出向量对应通道将被设置为全1,否则设置为全0。
Result_t vcage<q>_type(Vector1_t N, Vector2_t M);
Result_t vcale<q>_type(Vector1_t N, Vector2_t M);
Result_t vcagt<q>_type(Vector1_t N, Vector2_t M);
Result_t vcalt<q>_type(Vector1_t N, Vector2_t M);
- 按位与\或\非\异或操作
Result_t vand<q>_type(Vector1_t N, Vector2_t M);
Result_t vorr<q>_type(Vector1_t N, Vector2_t M);
Result_t vmvn<q>_type(Vector_t N);
Result_t veor<q>_type(Vector1_t N, Vector2_t M);

vmvn_s32 intrinsics 指令操作
- 元素与操作
// 按通道做与操作,为 true 时,将输出向量对应通道设置为全 1,否则设置为全 0
Result_t vtst<q>_type(Vector1_t N, Vector2_t M);
- 其他
// M 作为 mask,标识是否对 N 做清零操作。当 M 中某位为 1, 则将 N 中对应位清零
Result_t vbic<q>_type(Vector1_t N, Vector2_t M);// P 作为 mask,按位 select。当 P 中某位是 1 时,将选择 N 中对应位作为输出,否则选择 M
Result_t vbsl<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);
3.2.6 Floating-point
- 浮点数之间的转化, 以及浮点类型与整数类型之间的转化
// 单精度浮点转化为整数类型
Result_t vcvt<q>_type_f32(Vector_t N);// 整数类型转化为单精度浮点
Result_t vcvt<q>_f32_type(Vector_t N);// f16转化为f32
Result_t vcvt_f16_f32(Vector_t N);// f32转化为f16
Result_t vcvt_f32_f16(Vector_t N);
- 浮点类型的乘加操作
Result_t vfma<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);
- 浮点类型的乘减操作
Result_t vfms<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);

vfms intrinsics 指令操作
3.2.7 Permutation
- 向量提取组合操作
Result_t vext<q>_type(Vector1_t N, Vector2_t M, int n);

vextq_u8 intrinsics 指令操作
- 查表操作
Result_t vtbl[n]_type(Vector1_t N, Vector2_t M);
Result_t vtbx[n]_type(Vector1_t N, Vector2_t M, Vector3_t P);
- 向量翻转操作
Result_t vrev64<q>_type(Vector_t N);
Result_t vrev32<q>_type(Vector_t N);
Result_t vrev16<q>_type(Vector_t N);
vrev16<q>_type按照 16bit 为块,块内数据按照 8bit 为单位进行翻转 。
vrev32<q>_type按照 32bit 为块,块内数据按照 8bit,16bit 为单位进行翻转 。
vrev64<q>_type按照 64bit 为块,块内数据按照8bit, 16bit, 32bit为单位进行翻转 。

vrev16_s8, vrev32_s8 intrinsics 指令操作
- 旋转操作
旋转指令包含了两种矩阵旋转的指令,TRN1,TRAN2
Result_t vtrn1<q>_type(Vector1_t N, Vector2_t M);
Result_t vtrn2<q>_type(Vector1_t N, Vector2_t M);

vtrn1q_s32, vtrn2q_s32 intrinsics 指令操作
- 向量交织和解交织操作
// 交织操作
Result_t vzip<q>_type(Vector1_t N, Vector2_t M);// 解交织操作
Result_t vuzp<q>_type(Vector1_t N, Vector2_t M);

vzip_u8 intrinsics 指令操作
3.2.8 Miscellaneous
- 将同一个标量填充到每个向量通道
Result_t vcreate_type(Scalar_t N);
Resutl_t vdup_type(Scalar_t N);
Result_t vdup_n_type(Scalar_t N);
Result_t vdupq_n_type(Scalar_t N);
Result_t vmov_n_type(Scalar_t N);
Result_t vmovq_n_type(Scalar_t N);
- 将向量中某个通道的数据填充到指定的向量中
Result_t vdup<q>_lane_type(Vector_t N, int n);

vdup_lane_s32 intrinsics 指令操作
3.2.9 Data processing
- max\min操作
// 基本的 max, min
Result_t vmax<q>_type(Vector1_t N, Vector2_t M);
Result_t vmin<q>_type(Vector1_t N, Vector2_t M);// pairwise 类型的 max, min
Result_t vpmax_type(Vector1_t N, Vector2_t M);
Result_t vpmin_type(Vector1_t N, Vector2_t M);

vpmin_s16 intrinsics 指令操作
- 差的绝对值操作
// 基本的绝对值计算
Result_t vabs<q>_type(Vector_t N);// 差的绝对值操作
Result_t vabd<q>_type(Vector1_t N, Vector2_t M);// L(Long)类型, 差的绝对值
Result_t vabdl_type(Vector1_t N, Vector2_t M);// 差的绝对值,并和另一个向量相加
Result_t vaba<q>_type(Vector1_t N, Vector2_t M, Vector3_t P);// L(Long)类型, 差的绝对值,并和另一个向量相加, 输出是输入长度的两倍
Result_t vabal_type(Vector1_t N, Vector2_t M, Vector3_t P);
- 取反操作
// 基本的取反操作
Result_t vneg<q>_type(Vector_t N);// Q(Saturated)类型,带饱和的取反操作
Result_t vqneg<q>_type(Vector_t N);
- 按位统计 0 或 1 的个数
// 统计每个通道 1 的个数
Result_t vcnt<q>_type(Vector_t N);// 从符号位开始,统计每个通道中与符号位相同的位的个数,且这些位必须是连续的
Result_t vcls<q>_type(Vector_t N);// 从符号位开始,统计每个通道连续0的个数
Result_t vclz<q>_type(Vector_t N);
- 倒数和平方根求倒计算
// 对每个通道近似求倒
Result_t vrecpe<q>_type(Vector_t N);// 对每个通道使用 newton-raphson 求倒
Result_t vrecps<q>_type(Vector1_t N, Vector2_t M);// 对每个通道平方根近似求倒
Result_t vrsqrte<q>_type(Vector_t N);// 对每个通道使用 newton-raphson 平方根近似求倒
Result_t vrsqrts<q>_type(Vector1_t N, Vector2_t M);
- 向量赋值
// N(Narrow) 类型的赋值,取输入每个通道的高半部分,赋给目的向量
Result_t vmovn_type(Vector_t N);// L(long) 类型的赋值,使用符号拓展或者 0 拓展的方式,将输入通道的数据赋给输出向量
Result_t vmovl_type(Vector_t N);// QN(Saturated, Narrow) 类型的赋值,饱和的方式赋值,输出是输入宽度的两倍
Result_t vqmovn_type(Vector_t N);// QN(Saturated, Narrow) 类型的赋值,饱和的方式赋值,输出是输入宽度的两倍,而且输入为有符号数据,输出无符号
Result_t vqmovun_type(Vector_t N);
3.2.10 Type conversion
- 元素类型的重新解释
Result_t vreinterpret<q>_DSTtype_SRCtype(Vector1_t N);
- 两个 64bit 向量组合成一个 128bit 向量
Result_t vcombine_type(Vector1_t N, Vector2_t M);
- 提取 128bit 向量的高半部分或则低半部分
Result_t vget_high_type(Vector_t N);
Result_t vget_low_type(Vector_t N);

vget_low_s32 \ vget_high_s32 intrinsics 指令操作
四、NEON intrisics 指令在x86平台的仿真
为了便于 NEON 指令从 ARM 平台移植到 x86 平台使用,Intel 提供了一套转化接口 NEON2SSE,用于将 NEON 内联函数转化为 Intel SIMD(SSE) 内联函数。大部分 x86 平台 C/C++编译器均支持 SSE,因此只需下载并包含接口头文件NEON_2_SSE.h,即可在x86平台调试 NEON 指令代码。
#ifdef ARM_PLATFORM
# include <arm_neon.h>
#else
# include "NEON_2_SSE.h"
#endif
NEON2SSE 提供了 1700 多个 NEON 内联函数的转换接口,运算结果确保与 ARM 平台准确一致。
性能方面:
- 对于使用 128 位向量运算的 NEON 操作,NEON2SSE 在 x86 平台能得到与 ARM 类似的加速比;
- 如果使用 64 位向量做 NEON 运算,x86 平台的加速比将低于 ARM 平台。
五、 NEON指令的应用
本节将会结合实际应用场景介绍 NEON 指令的使用方法。
5.1 RGB de-interleave 加载 / interleave 存储
使用 vld3q 以解交织的方式加载 RGB 图像;vst3q 以交织的方式存储 RGB 图像。
// 输入地址为 in_ptr, 输出向量为 vec
uint8x16x3_t vec = vld3q(in_ptr);// 输出地址为 out_ptr, 输入为 uint8x16x3_t 类型的 RGB 向量
vst3q(out_ptr, vec);

load/store 示意图
5.2 查表操作
大多数的重排操作中,重排模式都是固定的,这在使用上带来了一定的局限性。
NEON 在常规重排指令外,支持使用TBL和TBX指令来完成任意模式的重排操作,这两条指令本身也是查表指令。
TBL和TBX输入参数介绍:- 向量类型的下标,通过下标向量到表中查找对应的元素。
- 向量类型的表,最多可以有 4 个寄存器向量值。
这两条指令使用下标向量到对应表中索引数据,并把找到的数据存放到输出向量中去。
TBL和TBX的不同在于:当没有索引值超过范围时,TBL返回 0,TBX保持原有目的数据不变。
// a表示table, b表示index, c表示结果
uint8x8_t c = vtbl2_u8(a, b)

vtbl2_u8 intrisics 操作
5.3 边缘处理
处理图像边缘时,经常会有使用常数填充边界的情况。
NEON 开发中,可以使用DUP指令将常数填充到向量中,然后使用EXT指令组建新向量。
例如 7x7 的 boxfilter,处理边界时需要填充 3 个像素的值。
- EXT指令还常常用于滤波向量的重组操作。
// 构造边界填充向量
uint8_t c_0 =0;
uint8x8_t v_c0 = v_dup_n_u8(c_0);// 构建v_1
uint8x8_t v_1 = vext_u8(v_c0, v_0, 5)// 使用 vext 构建边界向量,v0 表示从纵坐标为 0 起始的向量
uint8x8_t v_border = vext_u8(v_1, v_c0, 3)

边界扩展示意图
5.4 SAD操作
SAD(sum of absolute difference) 运算可以使用 NEON 指令来加速。
- 首先使用vabd做差的绝对值计算。
- 然后使用vdot将上面的结果做累加。
// 初始化 v_sum 和 v_c1
uint32x4_t v_sum = vmovq_n_u32(0);
uint8x16_t v_c1 = vmovq_n_u8(1);// v_src0, v_src1为两幅图的输入
// 将做差的绝对值计算
uint8x16_t v_abd_res = vabdq_u8(v_src0, v_src1);// 做 vdot操作
v_sum = vdotq_u32(v_sum , v_abd_res, v_c1);
...
// 将最后的结果累加
uint32_t res = vaddvq_u32(v_sum);
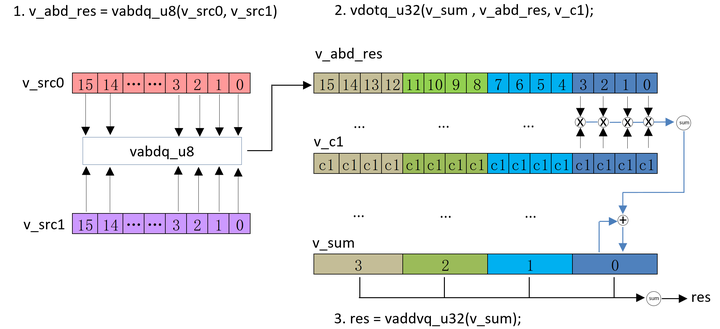
NEON SAD 操作示意图
六、总结
本文主要介绍了 NEON 指令相关的知识,首先通过讲解 arm 指令集的分类,NEON寄存器的类型,树立基本概念。然后进一步梳理了 NEON 汇编以及 intrinsics 指令的格式。最后结合指令的分类,使用例子讲述 NEON 指令的使用方法。
七、附录
参考资料
[1] ARM Neon Programmer's Guide
[2] ARM NEON programming quick reference
[3] ARM Architecture Reference Manual Armv8, for A-profile architecture
[4] https://developer.arm.com/architectures/instruction-sets/intrinsics/
🌈我的分享也就到此结束啦🌈
如果我的分享也能对你有帮助,那就太好了!
若有不足,还请大家多多指正,我们一起学习交流!
📢未来的富豪们:点赞👍→收藏⭐→关注🔍,如果能评论下就太惊喜了!
感谢大家的观看和支持!最后,☺祝愿大家每天有钱赚!!!欢迎关注、关注!
