JNA关系映射表
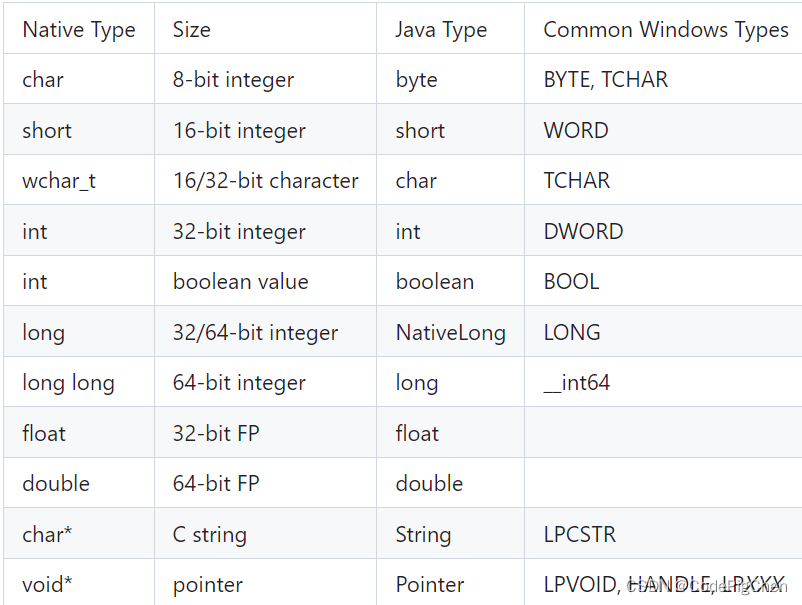
使用案列
注意
- JNA只支持C方式的dll
- 使用C++的char* 作为返回值时,需要返回的变量为malloc分配的地址
- C++的strlen函数只获得除/0以外的字符串长度
代码示例
C++代码
// 下列 ifdef 块是创建使从 DLL 导出更简单的
// 宏的标准方法。此 DLL 中的所有文件都是用命令行上定义的 TESTJNA_EXPORTS
// 符号编译的。在使用此 DLL 的
// 任何项目上不应定义此符号。这样,源文件中包含此文件的任何其他项目都会将
// TESTJNA_API 函数视为是从 DLL 导入的,而此 DLL 则将用此宏定义的
// 符号视为是被导出的。
#ifdef TESTJNA_EXPORTS
#define TESTJNA_API __declspec(dllexport)
#else
#define TESTJNA_API __declspec(dllimport)
#endif
#include<vector>
#include<string>
#include<nlohmann/json.hpp>using json = nlohmann::json;//头文件extern "C" TESTJNA_API const char* testJNAPlusJson(int arr[], const char* arr2);//cpp
const char* testJNAPlusJson(int arr[], const char* arr2)
{json j = json::parse(arr2);std::vector<std::vector<int>> resVector = j.get<std::vector<std::vector<int>>>();//序列化为字符串json ressd(resVector);std::string dasd = ressd.dump();auto suibian = dasd.length()+1;//实际的字符串长度const char* hhh = dasd.c_str();//c字符串char* resfinal = (char*)malloc(suibian);// char* 返回值分配的strcpy_s(resfinal, suibian,hhh);free(resfinal );return resfinal;
}
java代码
public class JNATestPlus { public interface CTest extends Library { CTest INSTANCE = (CTest) Native.load("TESTJNA.dll",CTest.class); String testJNAPlusJson(int[] arr, String arr2); } static { URL resource = JNATestPlus.class.getClassLoader().getResource("./libs/TESTJNA.dll"); String path = resource.getPath(); System.load(path); } public static void main(String[] args) { int[] arr = {1,2}; int[][] arr2 ={{1,2},{1,2}}; String s2 = JSON.toJSONString(arr2); String s1 = CTest.INSTANCE.testJNAPlusJson(arr, s2); System.out.println(s1); }
}

